Финансово-экономический факультет
Специальность: «ЭО»
Дисциплина: Линейная алгебра (1 курс)
Экзаменационный билет № 1
Учебный 2011/2012 год
I. Теоретические вопросы
ТA1. Векторы a = e ( x ) – 3 e ( y ) и b = 6 e ( x ) + 2 e ( y ) + e (z) являются …
A. ортогональными
B. коллинеарными
C. линейно зависимыми
D. равными
ТA2. Набор переменных (x 1, x 2,…, xn), который удовлетворяет всем ограничениям задачи
линейного программирования, называется …
A. совместным решением задачи линейного программирования
B. определенным решением задачи линейного программирования
C. оптимальным решением задачи линейного программирования
D. допустимым решением задачи линейного программирования
ТА3. Количество переменных yi в двойственной задаче равно
A. количеству неравенств xj ≥ 0 в прямой задаче
B. количеству неравенств в прямой задаче (кроме неравенств xj ≥ 0)
C. количеству коэффициентов при переменных у целевой функции в прямой задаче
D. количеству всех неравенств в прямой задаче, включая неравенства xj ≥ 0
ТB1. Какие из перечисленных равенств являются верными для произвольных векторов a и b?
A. (a, b) = (b, a)
B. (a, b) = – (b, a)
C. [ a, b ] = [ b, a ]
D. [ a, b ] = – [ b, a ]
ТB2. Какие из перечисленных функций могут быть целевыми функциями для задачи линейного
программирования?
A. 
B. 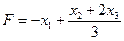
C. 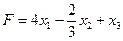
D. 
ТС. Можно ли задачу линейного программирования, заданную в каноническом виде, привести
к стандартному виду? Если можно, то каким образом?
II. Практические задания
PА1. Имеется задача линейного программирования:

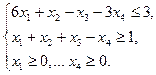
Составьте задачу, двойственную к данной.
PА2. Найдите уравнение прямой, проходящей через точки A (6,7) и B (2,1).
PВ1. Решите задачу линейного программирования графическим методом.

PВ2. Ищется максимум целевой функции f симплексным методом. На очередном шаге решения
получены выражения базисных переменных x 1, x 3 и целевой функции через свободные
переменные x 2, x 4 и x 5:
x 1 = 8 + x 2 + x 4 – 2 x 5;
x 3 = 10 + x 2 + x 4 – 5 x 5;
f = 8 – 4 x 2 – x 4 + 7 x 5.
Укажите, какие переменные будут базисными на следующем шаге решения.
PC1. Найдите векторное произведение векторов a = e ( x ) – 3 e ( y ) и b = 6 e ( x ) + 2 e ( y ) + e (z).
PC2. Решите задачу линейного программирования.
 ,
,
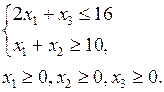
Заведующий кафедрой _____________________/Феклин В.Г./
| МИНИСТЕРСТВО ФИНАНСОВ РОССИЙСКОЙ ФЕДЕРАЦИИ ВСЕРОССИЙСКАЯ ГОСУДАРСТВЕННАЯ НАЛОГОВАЯ АКАДЕМИЯ |
Финансово-экономический факультет
Специальность: «ЭО»
Дисциплина: Линейная алгебра (1 курс)
Экзаменационный билет № 2
Учебный 2011/2012 год
I. Теоретические вопросы
ТA1. Векторы a = 3 e ( x ) – 4 e ( y ) – e ( z ) и b = –6 e ( x ) + 8 e ( y ) + 2 e (z) являются …
A. ортогональными
B. ортонормированными
C. коллинеарными
D. равными
ТA2. В каком случае задача математического программирования называется задачей линейного
программирования?
A. если целевая функция линейна относительно входящих в задачу переменных
B. если функции, входящие в систему ограничений, линейны относительно входящих в
задачу переменных
C. если целевая функция и функции, входящие в систему ограничений, линейны
относительно входящих в задачу переменных
D. задача линейного программирования не относится к задаче математического
программирования
ТA3. Коэффициентами целевой функции двойственной задачи являются
A. коэффициенты при дополнительных переменных прямой задачи
B. коэффициенты целевой функции прямой задачи
C. коэффициенты при основных переменных прямой задачи
D. свободные члены системы ограничений прямой задачи
ТB1. Какие из перечисленных равенств выполняются для координатных векторов e ( x ), e ( y ) и e (z)?
A. (e ( x ), e ( y ))= 0
B. (e (x), e (y))= e (z)
C. [ e (x), e (y)]= e (z)
D. [ e (x), e (y)]= 0
ТB2. Какие из перечисленных функций могут быть целевыми функциями некоторой задачи
линейного программирования с тремя переменными?
A. 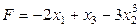
B. 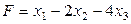
C. 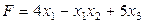
D. 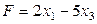
ТС. Можно ли задачу линейного программирования, заданную в стандартном виде, привести к
каноническому виду? Если можно, то каким образом?