PА1. Имеется задача линейного программирования:
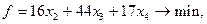
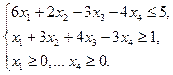
Составьте задачу, двойственную к данной.
PА2. Найдите уравнение прямой, проходящей через точки A (–1,11) и B (1,3).
PВ1. Решите задачу линейного программирования графическим методом.
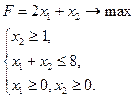
PВ2. Ищется минимум целевой функции f симплексным методом. На очередном шаге решения
получены выражения базисных переменных x 2, x 3 и целевой функции через свободные
переменные x 1, x 4 и x 5:
x 2 = 3 + 2 x 1 – 3 x 4 + 6 x 5;
x 3 = 10 + x 2 – x 4 – 5 x 5;
f = 8 – x 1 – 3 x 4 + 5 x 5.
Укажите, какие переменные будут базисными на следующем шаге решения.
PC1. Найдите векторное произведение векторов a = e ( x ) + 6 e ( y ) + e (z) и b = –4 e ( x ) + 2 e ( y ) – e (z).
PC2. Решите задачу линейного программирования.
,
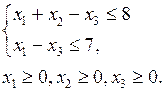
Заведующий кафедрой _____________________/Феклин В.Г./
| МИНИСТЕРСТВО ФИНАНСОВ РОССИЙСКОЙ ФЕДЕРАЦИИ ВСЕРОССИЙСКАЯ ГОСУДАРСТВЕННАЯ НАЛОГОВАЯ АКАДЕМИЯ |
Финансово-экономический факультет
Специальность: «ЭО»
Дисциплина: Линейная алгебра (1 курс)
Экзаменационный билет № 3
Учебный 2011/2012 год
I. Теоретические вопросы
ТA1. Векторы a = – e ( y ) и b = e (z) являются …
A. линейно зависимыми
B. коллинеарными
C. ортогональными
D. равными
ТA2. Как связаны между собой число переменных n (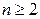
) и число ограничений m в задаче
линейного программирования с неотрицательными переменными?
A.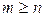 
B. 
C. 
D. не связаны
ТА3. Если f (x) – целевая функция задачи линейного программирования на минимум,
а z (y) – целевая функция двойственной к ней задачи, то
A. min f (x) = min z (y)
B. min f (x) = max z (y)
C. f (x) £ z (y)
D. f (x) ≥ z (y)
ТB1. Какие из перечисленных равенств выполняются для координатных векторов e ( x ), e ( y ) и e (z)?
A. (e (x), e (y))= –(e (x), e (y))
|
|
B. (e (x), e (y))= (e (x), e (y))
C. [ e (x), e (y)]= [ e (x), e (y)]
D. [ e ( x ), e ( y )]= –[ e ( x ), e ( y )]
ТB2. Какие из перечисленных функций могут быть целевой функцией некоторой задачи линейного
программирования с тремя переменными?
A.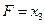 
B. 
C. 
D.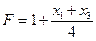 
ТС. Задача линейного программирования имеет 4 переменных и 2 ограничения (не считая условий
неотрицательности переменных). Можно ли такую задачу решить, не используя симплексный
метод решения. Если можно, то каким образом?
II. Практические задания
PА1. Имеется задача линейного программирования:
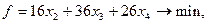
Составьте задачу, двойственную к данной.
PА2. Найдите уравнение прямой, проходящей через точки A (7, –1) и B (–17,2).
PВ1. Решите задачу линейного программирования графическим методом.
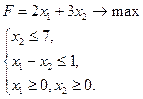
PВ2. Ищется максимум целевой функции f симплексным методом. На очередном шаге решения
получены выражения базисных переменных x 4, x 5 и целевой функции через свободные
переменные x 1, x 2 и x 3:
x 1 = 1 + x 1 – 4 x 2 – 5 x 3;
x 3 = 2 + x 1 + 3 x 3;
f = 30 – x 1 + x 2 – x 3.
Укажите, какие переменные будут базисными на следующем шаге решения.
PC1. Найдите векторное произведение векторов a = e ( x ) + 5 e (z) и b = – e ( x ) + e ( y ) – 2 e (z).
PC2. Решите задачу линейного программирования.
,
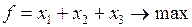Заведующий кафедрой _____________________/Феклин В.Г./
| МИНИСТЕРСТВО ФИНАНСОВ РОССИЙСКОЙ ФЕДЕРАЦИИ ВСЕРОССИЙСКАЯ ГОСУДАРСТВЕННАЯ НАЛОГОВАЯ АКАДЕМИЯ |
Финансово-экономический факультет
Специальность: «ЭО»
Дисциплина: Линейная алгебра (1 курс)