Изложение метода (описание алгоритма)

Параметрами метода являются:

• коэффициент отражения , обычно выбирается равным 1.
• коэффициент сжатия , обычно выбирается равным 0.5.
• коэффициент растяжения , обычно выбирается равным 2.

Инициализация. Произвольным образом выбирается точка , образующие симплекс n-мерного пространства. В этих точках вычисляются значения функции: . Вершины симплекса можно найти, воспользовавшись приведенной ниже таблицей

Вершины	Координаты
			.....................
				.....................
	g1	g	g	.....................	g	g	g
. . . .	. . . .	. . . .	. . . .		. . . .	. . . .	. . . .
n-2	g	g	g	.....................	g1	g	g
n-1	g	g	g	.....................	g	g1	g
n	g	g	g	.....................	g	g	g1

где

 

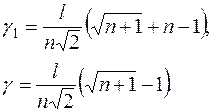
1. Сортировка. Из вершин симплекса выбираем три точки: с наибольшим (из выбранных) значением функции , 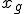со следующим по величине значением и с наименьшим значением функции . Целью дальнейших манипуляций будет уменьшение по крайней мере .

2. Найдём центр тяжести всех точек, за исключением . Вычислять 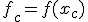не обязательно.

3. Отражение. Отразим точку относительно с коэффициентом (при это будет центральная симметрия, в общем случае — гомотетия), получим точку и вычислим в ней функцию: . Координаты новой точки вычисляются по формуле

Анализируют результат отображения, сравнивая значение функции в отображенной вершине с ее значениями в вершинах предыдущего сим­плекса (детализация алгоритма в пункте 4):

а) если при этом значении функции в новой вершине оказалось меньше, чем наилучшее значение предыдущего симплекса, т.е. , то проводят растяжение симплекса увеличивая b (b>1) обычно в два раза от отраженной вершины до центра тяжести Если после операции растяжения значение функции в новой точке уменьшится, то эта вершина принимается за вершину нового симплекса, если же увеличивается, то в качестве новой вершины берется точка, полученная после отражения

b) Когда значение функции в отраженной вершине меньше чем в наихудшей вершине, но больше чем во всех остальных, то выполняют операцию сжатия с коэффициентом b<1 (обычно b=0.5)

с) Если значение функции в отраженной точке больше чем в наихудшей вершине предыдущего симплекса, то производят редукцию (уменьшение размеров симплекса обычно в два раза), т.е. координаты все вершин симплекса сдвигают на половину расстояния до наилучшей точки

В качестве критерия остановки авторы алгоритма рекомендуют средне­квадратичную величину разности значений функции в вершинах симплекса и

 

среднего ее значения, т.е. , где e- заданная точность.

 

4. Далее сравниваем значение со значениями :

4а. Если , то производим растяжение. Новая точка и значение функции .

Если , то заменяем точку на и заканчиваем итерацию (на шаг 8).

Если , то заменяем точку на и заканчиваем итерацию (на шаг 8).

4b. Если , то заменяем точку на и переходим на шаг 8.

4с. Если , то меняем обозначения (и соответствующие значения функции) местами и переходим на шаг 5.

4d. Если , то переходим на шаг 5.

5. Сжатие. Строим точку и вычисляем в ней значение .

6. Если , то заменяем точку на и переходим на шаг 8.

7. Если , то производим сжатие симплекса — гомотетию к точке с наименьшим значением : для всех требуемых точек .

8. Последний шаг — проверка сходимости. Может выполняться по-разному, например, оценкой дисперсии набора точек. Суть проверки заключается в том, чтобы проверить взаимную близость полученных вершин симплекса, что предполагает и близость их к искомому минимуму. Если требуемая точность ещё не достигнута, можно продолжить итерации с шага 1.

 

Графическое представление описанного выше алгоритма приведено на рисунке.

 

 

Анализ метода

Изучение сходимости алгоритма Нелдера-Мида является трудной математической задачей. Известные результаты о сходимости симплекс-методов основаны на следующих предположениях:

• Симплекс не должен вырождаться при итерациях алгоритма

• На гладкость функции накладываются некоторые условия

В общем случае для метода Нелдера-Мида не выполняются сразу оба эти предположения, а следовательно, об условиях сходимости известно весьма мало. МакКиннон в 1998 году описал семейство строго выпуклых функций и класс начальных симплексов в двухмерном пространстве, для которых все вершины рабочего симплекса сходятся не к оптимальной точке. В 1998 году Лагариас опубликовал статью, в которой он исследовал сходимость метода в одно- и двухмерном пространствах для некоторых строго выпуклых функций с ограниченными поверхностями уровня.

Алгоритм Нелдера-Мида дает сильное уменьшение значение функции уже при первых нескольких итерациях и быстро достигает необходимой точности. Как правило, алгоритм производит одно или два вычисления функции на каждой итерации, если не учитывать сжатие, которое редко используется на практике. Это крайне важно в тех ситуациях, когда вычисление значений функции очень дорого или же требует много времени. Для подобных задач алгоритм Нелдера-Мида гораздо эффективнее многих других методов, требующих вычисления не менее значений функции на каждой итерации.

Главными преимуществами алгоритма являются его простота и эффективность.

С другой стороны, в силу отсутствия теории сходимости, на практике метод может приводить к неверному ответу даже для гладких функций. Также возможна ситуация, когда рабочий симплекс находится далеко от оптимальной точки, а алгоритм производит большое число итерации, при этом мало изменяя значения функции. Эвристический метод решения этой проблемы заключается в запуске алгоритма несколько раз и ограничении числа итераций.

ТЕКСТ ПРОГРАММЫ

Текст программы разработан и отлажен на языке C/C++ в среде Microsoft Visual Studio 2015., приводится целиком, с комментариями и функциями вызова, готовый к компиляции и выполнению.

 

// ConsoleApplication6.cpp: определяет точку входа для консольного приложения.

//

 

#include "stdafx.h"

#include <iostream>

#include <math.h>

using namespace std;

 

const int N_DIM = 2;

int Iters;

 

struct Vertex {

double x, y;

Vertex()

{

x = y = 0;

}

Vertex(double X, double Y)

{

x = X;

y = Y;

}

Vertex operator+=(const Vertex & v)

{

x += v.x;

y += v.y;

return *this;

}

Vertex operator/(double q)

{

return *(new Vertex(x / q, y / q));

}

friend Vertex operator * (Vertex v, double d)

{

return *(new Vertex(v.x*d, v.y*d));

}

friend Vertex operator - (Vertex v1, Vertex v2)

{

return *(new Vertex(v1.x - v2.x, v1.y - v2.y));

}

friend Vertex operator + (Vertex v1, Vertex v2)

{

return *(new Vertex(v1.x + v2.x, v1.y + v2.y));

}

friend double Dist(Vertex v1, Vertex v2)

{

return sqrt((v1.x - v2.x)*(v1.x - v2.x) + (v1.y - v2.y) * (v1.y - v2.y));

}

public:

void Out()

{

cout << "x=" << x << ",y=" << y << endl;

}

};

 

 

class Simplex {

public:

Vertex v[N_DIM + 1];

Simplex(Vertex z[])

{

for (int i = 0; i <= N_DIM; i++)

v[i] = z[i];

}

public:

void Out()

{

for (int i = 0; i <= N_DIM; i++)

v[i].Out();

cout << endl;

}

};

 

bool QuitCase(Simplex* s)

{

for (int i = 0; i <= N_DIM; i++)

for (int j = 0; j <= N_DIM; j++)

if (Dist(s->v[i], s->v[j])>0.01)

return false;

return true;

}

 

double Func(Vertex v)

{

// Овражная функция Розенброка

return 100 * (v.y - v.x*v.x) * (v.y - v.x*v.x) + (1 - v.x) * (1 - v.x);

// return 100 * (v.y - v.x*v.x) * (v.y - v.x*v.x) + (1 - v.x) * (1 - v.x);

}

void Sort(Simplex* smpl, double f[])

{

double f1;

Vertex v1;

 

for (int i = 1; i <= N_DIM; i++)

for (int j = i; j >= 1; j--)

if (f[j - 1]>f[j])

{

f1 = f[j];

v1 = smpl->v[j];

f[j] = f[j - 1];

smpl->v[j] = smpl->v[j - 1];

f[j - 1] = f1;

smpl->v[j - 1] = v1;

}

else break;

}

 

double NMA(Simplex* smpl, double alpha = 1.0, double beta = 0.5, double gamma = 2.0)

{

double f[N_DIM + 1];

double f_h, f_g, f_l, f_r, f_e, f_s, tempD;

Vertex x_h, x_g, x_l, x_r, x_e, x_s, x_c, tempV;

int i;

bool flag;

 

for (i = 0; i <= N_DIM;i++) f[i] = Func(smpl->v[i]); // Вычисление значений функции на начальном симплексе

 

while (!QuitCase(smpl)) // Проверка на условие выхода

{

Iters++;

 

// Шаг 1. Сортировка

Sort(smpl, f);

x_h = smpl->v[N_DIM]; f_h = f[N_DIM];

x_g = smpl->v[N_DIM - 1]; f_g = f[N_DIM - 1];

x_l = smpl->v[0]; f_l = f[0];

 

// Шаг 2. Вычисление центра тяжести симплекса

x_c.x = x_c.y = 0;

for (i = 0; i<N_DIM; i++) x_c += smpl->v[i];

x_c = x_c / N_DIM;

 

// 3Шаг. Отражение

x_r = x_c * (1 + alpha) - x_h * alpha; f_r = Func(x_r);

 

// Шаг 4.

if (f_r <= f_l)

{ // Шаг 4a.

x_e = x_c * (1 - gamma) + x_r * gamma;

f_e = Func(x_e);

if (f_e < f_l)

{

smpl->v[N_DIM] = x_e;

f[N_DIM] = f_e;

}

else

{

smpl->v[N_DIM] = x_r;

f[N_DIM] = f_r;

}

}

if ((f_l < f_r) && (f_r <= f_g))

{ // Шаг 4.b

smpl->v[N_DIM] = x_r;

f[N_DIM] = f_r;

}

flag = false;

if ((f_h >= f_r) && (f_r > f_g))

{ // Шаг 4c.

flag = true;

tempD = f_h;

tempV = x_h;

smpl->v[N_DIM] = x_r;

f[N_DIM] = f_r;

x_r = tempV;

f_r = tempD;

}

// Шаг 4d.

if (f_r > f_h) flag = true;

if (flag)

{ // Шаг 5. Сжатие

x_s = x_h * beta + x_c * (1 - beta);

f_s = Func(x_s);

if (f_s < f_h)

{ // 6.

tempD = f_h;

tempV = x_h;

smpl->v[N_DIM] = x_s;

f[N_DIM] = f_s;

x_s = tempV;

f_s = tempD;

}

else

{ // Шаг 7. Глобальное сжатие

for (i = 0; i <= N_DIM; i++)

smpl->v[i] = x_l + (smpl->v[i] - x_l) / 2;

}

}

}

return f_l;

}

 

 

int _tmain(int argc, _TCHAR* argv[])

{

char c;

Vertex v1(10, 9), v2(10, -2), v3(21, 1);

Vertex s[3];

s[0] = v1;

s[1] = v2;

s[2] = v3;

Simplex* sm = new Simplex(s);

Iters = 0;

double accuracy = NMA(sm);

 

cout << "Accuracy is " << accuracy << " in " << Iters << endl;

 

cin >> c;

return 0;

}

РЕЗУЛЬТАТЫРАСЧЕТОВ

В качестве числового эксперимента метод Нелдера-Мида был применен для вычисления минимума функции Розенброка:

для которой и . В качестве начального прибилжения был взят симплекс .

Ниже приведена таблица промежуточных результатов после каждых 10 итераций алгоритма.

Число итераций	Координаты первой точки симплекса	Координаты второй точки симплекса	Координаты третьей точки симплекса
	x=2.78; y=7.55;	x=2.39; y=6.39;	x=1.73; y=6.87;	6.725	1479.400
	x=2.63; y=6.96;	x=2.70; y=7.29;	x=2.64; y=6.88;	2.769	3.225
	x=2.24; y=4.94;	x=2.35; y=5.50;	x=2.42; y=5.86;	1.823	2.017
	x=1.90; y=3.58;	x=1.83; y=3.38;	x=1.97; y=3.89;	0.821	0.996
	x=1.51; y=2.28;	x=1.53; y=2.36;	x=1.57; y=2.47;	0.273	0.327
	x=1.20; y=1.42;	x=1.23; y=1.51;	x=1.27; y=1.61;	0.050	0.079
	x=0.99; y=0.97;	x=1.01; y=1.02;	x=0.96; y=0.93;	0.000	0.003

Итоговое количество итераций 79. Вычисленный минимум функционала равен .

 

 

Выводы

Для тестовой функции Розенброка (функция овражного типа) метод Нелдера - Мида сходится относительно хорошо – после 79 итераций.

 

Литература

1. Красовский Г. И., Филаретов Г. Ф. Планирование эксперимента.— Мн.: Изд-во БГУ,

1982.