Постановка математической задачи

КУРСОВОЙ ПРОЕКТ (РАБОТА)

по дисциплине "Планирование измерительного эксперимента"

Тема курсового проекта (работы) «Планирование экстремального эксперимента»

 

Студент группы КПМО-01-17Смирнов С.П. /________________

(учебная группа, фамилия, имя, отчество студента) (подпись студента)

Руководитель курсового проекта к.т.н, доцент, Пастушков А.А. /______________

(должность, звание, ученая степень) (подпись руководителя)

Рецензент (при наличии) ______________________ (должность, звание, ученая степень) (подпись рецензента)

 

 

Работа представлена к защите «___» ___________ 20__г.

 

Допущен к защите «___» ___________ 20__г.

 

Москва, 2018

МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА – Российский технологический университет» РТУ МИРЭА Институт кибернетики Кафедра информационных систем       УТВЕРЖДАЮ   Заведующий кафедрой______________ В.К. Батоврин     «____» __________20___ г. ЗАДАНИЕ на выполнение курсовой работы (проекта) по дисциплине "Планирование измерительного эксперимента"   Обучающийся Смирнов С.П.   Шифр 17К0793 Группа КПМО-01-17 Вариант № 6 1. Тема:Планирование экстремального эксперимента 2. Исходные данные: 1. Разработать программу на языке С/C++ для планирования экстремального эксперимента методом Нелдера – Мида.     3. Перечень вопросов, подлежащих разработке, и обязательного графического материала: 1. Текст программы на языке С/C++ 2. Результаты работы программы с функцией Розенброка ()     4.Срок представления к защите курсовой работы до «___» _______20___ г.   Задание на курсовую Работу (проект) выдал «___»______20___ г. ____________________ (Пастушков А.А.) Задание на курсовую Работу (проект) получил «___»______20___ г. _____________________ (Смирнов С.П.)                 МИНОБРНАУКИ РОССИИ

 

ПЛАНИРОВАНИЕ ЭКСТРЕМАЛЬНЫХ ЭКСПЕРИМЕНТОВ

ВВЕДЕНИЕ

Задача оптимизации - одна из наиболее важных и распространенных задач, встречающихся в практике на­учных и инженерных исследований как теоретического, так и прикладного характера. Определение наилучших, в некотором смысле, условий, решений, значений парамет­ров, уровней факторов является во многих случаях основ­ной целью ученого-исследователя, инженера проектировщика или специалиста технолога. В частности, такого рода оптимизационные проблемы возникают:

а) при управлении различными технологическими процессами, агрегатами, установками, где необходимо достижение максимальной производительности при наи­лучшем качестве и минимальных затратах;

б) при проектировании разнообразных инженерных устройств, приборов, схем, когда требуется подобрать та­кую комбинацию параметров, которая соответствовала бы наивысшим эксплуатационным характеристикам про­ектируемого аппарата;

в) при создании новых образцов продукции, сплавов, смесей, при синтезе химических веществ, обладающих наилучшими свойствами (скажем, максимальной проч­ностью, если речь идет о строительных материалах, или наибольшей активностью - для катализатора и т. п.);

г) наконец, к оптимизационным сводятся, в конечном итоге, многие задачи чисто вычислительного характера, например определение регрессионной модели методом наименьших квадратов или же численное построение пла­на эксперимента, оптимального в соответствии с выбран­ным критерием.

С математической точки зрения задача оптимизации формулируется следующим образом: найти значения управляемых факторов

объекта исследования, при которых его отклик Y (целевая функция, критерий оптимизации) достигает сво­его экстремального значения 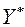(минимума или мак­симума в зависимости от постановки задачи):

Экстремальная точка во мно­гих случаях должна находиться с учетом определенных ограничений на X, которые могут принимать различную форму (ограничения на допустимые значения отдельных факторов, совокупность значений нескольких факторов, в виде равенств или неравенств и т. д.).

Всю совокупность методов оптимизации можно раз­бить на два основных класса:

1) теоретические методы, применяемые в ситуациях, где задача полностью определена с математической точ­ки зрения и по своему характеру допускает применение одного из известных аналитических методов оптимиза­ции: дифференциального или вариационного исчисления, линейного, целочисленного или динамического програм­мирования и т. д.

2) экспериментальные методы, используемые в усло­виях, когда функция отклика неизвестна и имеется возможность измерить значения У при различных комби­нациях величин факторов . Такая ситуация характерна как для исследования различного рода фи­зических объектов, так и для задач теоретического пла­на, если аналитические методы по тем или иным причи­нам оказываются непригодными то не остается ничего другого, как использовать численные методы решения, т. е. тоже своего рода экспериментальный метод, где эксперименты проводятся, например, на вычислительной машине. Главное отличие подобных задач от оптимизационных процедур чисто вычислительного плана - присутствие неконтролируемых факторов, т. е. наличие шума случай­ного характера, а также, может быть, детерминирован­ного дрейфа. В этой связи на первый план выступают во­просы эффективности различных методов оптимизации при наличии помех, сходимости алгоритмов, точности их функционирования в данных условиях.

Рассматриваемые методы экспериментальной оптими­зации можно разделить на две группы: 1) поисковые и 2) основанные на предварительном получении эмпириче­ской модели объекта, описывающей его поведение в об­ласти оптимума.

В поисковых методах осуществляется последователь­ное локальное изучение поверхности отклика. Экстре­мальное значение тогда достигается с помощью последо­вательных процедур, включающих в себя:

а) определение по результатам специально спланиро­ванного эксперимента направления движения из некото­рой данной точки, в окрестностях которой проводится эксперимент; это направление, естественно, зависит от локальных свойств поверхности отклика вблизи дайной точки и в принципе определяется таким образом, чтобы продвижение в найденном направлении приводило к зна­чениям функции отклика, более близким к оптимальным по сравнению со значением в исходной точке;

б) организацию движения в найденном направлении;

в) многократное повторение указанных этапов до до­стижения точки оптимума.

В соответствии с конкретными условиями экспери­ментирования целесообразно выделить две разновидно­сти поисковых методов оптимизации, предназначенных для использования 1) в лабораторных условиях и 2) в промышленности. Подобное разделение обусловлено ря­дом существенных отличий в организации эксперимен­тальной деятельности, связанных, прежде всего с тем об­стоятельством, что в промышленных условиях необходи­мо решать задачу оптимизации наряду с выпуском гото­вой продукции, т. е. без каких-либо значительных нару­шений технологического режима.

В дальнейшем будем предполагать, что:

а) объект исследования - статический;

б) функция отклика - унимодальная;

в) везде, где это необходимо, и в частности в методах оптимизации, использующих регрессионные модели, вы­полняются предпосылки регрессионного анализа. Кроме того, если специально не оговаривается про­тивное, считается, что объект исследования унимодальный, стационарный (без наличия временного дрейфа), какие-либо ограничения на возможные значения отдель­ных факторов или их комбинаций отсут­ствуют.

 

МЕТОД НЕЛДЕРА-МИДА (деформируемых многогранников)

Метод Нелдера-Мида является развитием симплексного метода Спендли, Хекста и Химсворта. Выпуклая оболочка множества -й равноудаленной точки в -мерном пространстве называется регулярным симплексом. Эта конфигурация рассматривается в методе Спендли, Хекста и Химсворта. В двухмерном пространстве регулярным симплексом является правильный треугольник, а в трехмерном - правильный тетраэдр. Идея метода состоит в сравнении значений функции в вершинах симплекса и перемещении симплекса в направлении оптимальной точки с помощью итерационной процедуры. В симплексном методе, предложенном первоначально, регулярный симплекс использовался на каждом этапе. Нелдер и Мид предложили несколько модификаций этого метода, допускающих, чтобы симплексы были неправильными. В результате получился очень надежный метод прямого поиска, являющийся одним из самых эффективных при .

Главными особенностями алгоритма можно назвать следующие:

• Метод Нелдера-Мида не накладывает ограничений на гладкость функции
• Данный метод явялется эффективным при низкой скорости вычисления минимизируемой функции. Как правило, на каждой итерации происходит вычисление значения функции не более чем в 3 точках.
• Алгоритм может расходиться даже на гладких функциях.

Постановка математической задачи

Задачей оптимизации называется задача поиска экстремума функции, заданной на некотором множетсве.

(1.1)

.

Как правило, под задачей оптимизации также подразумевается поиск элемента , при котором целевая функция достигает экстремума.

(1.2)

Для того, чтобы корректно поставить задачу оптимизации необходимо задать:

1. Допустимое множество
2. Целевую функцию
3. Критерий поиска (max или min)

Тогда решить задачу 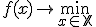означает одно из:

1. Показать что
2. Показать, что целевая функция не ограничена.
3. Найти
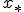
4. Если не существует 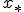, то найти

Если допустимое множество , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.

Рассматриваемая задача

Метод Нелдера-Мида, также известный как метод деформируемого многогранника, — метод безусловной оптимизации вещественной функции от нескольких переменных. Иными словами на допустимое множество накладываются следующие ограничения:

.

Кроме того, одним из главных преимуществ данного метода является то, что в нем не используется градиента целевой функции, что позволяет применять его к негладким функциям. Метод Нелдера-Мида использует понятие симплекса -мерного пространства'.

Множество называется выпуклым, если .

Выпуклой оболочкой множества 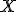называется наименьшее выпуклое множество такое, что

Симплексом или -симплексом называется выпуклая оболочка множества точек.

Например:

1-симплексом является отрезок

2-симплексом является треугольник

3-симплексом является тетраэдр.