Даны координаты трех точек: А (3; 0; –5), В (6; 2; 1), С (12; –12; 3).
Требуется: 1) записать векторы 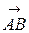 и и  в системе орт и найти модули этих векторов; 2) найти угол между векторами в системе орт и найти модули этих векторов; 2) найти угол между векторами 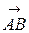 и и  ; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору ; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору 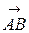 . .
|
Решение:
1) Найдем координаты вектора 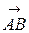 , подставив в формулу (11) координаты точек А и В, и запишем разложение этого вектора по ортам (13):
, подставив в формулу (11) координаты точек А и В, и запишем разложение этого вектора по ортам (13):
 .
.
Подобным образом
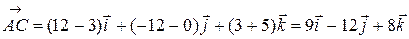 .
.
Модули векторов 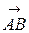 и
и  найдем, подставляя их координаты в формулу (12):
найдем, подставляя их координаты в формулу (12):
 ,
,  .
.
2) Найдем косинус угла φ между векторами 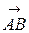 и
и  . Для этого вычислим их скалярное произведение по формуле (14):
. Для этого вычислим их скалярное произведение по формуле (14):
 .
.
Тогда по формуле (16)
 , φ ≈ 64˚37΄ ≈1,13 рад.
, φ ≈ 64˚37΄ ≈1,13 рад.
3) По условию задачи искомая плоскость проходит через точку С(12; –12; 3) перпендикулярно вектору  . Подставляя в (17) А= 3, В= 2, С= 6, х0= 12, у0= −12, z0= 3, получим:
. Подставляя в (17) А= 3, В= 2, С= 6, х0= 12, у0= −12, z0= 3, получим:
3(х – 12) +2 (y + 12) + 6(z – 3) = 0,
или 3х + 2у + 6z – 30 = 0 – искомое уравнение плоскости.
Задача 3.
Теоретические сведения.
Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Условием компланарности трех векторов  ,
, 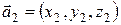 ,
,  является равенство нулю их смешанного произведения:
является равенство нулю их смешанного произведения:
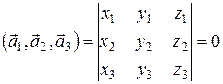 . (18)
. (18)
Три вектора образуют базис в том случае, если они некомпланарны.
Если для векторов 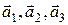 выполняется условие
выполняется условие  , то они образуют базис, и любой четвертый вектор
, то они образуют базис, и любой четвертый вектор 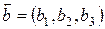 может быть представлен разложением по этому базису в виде
может быть представлен разложением по этому базису в виде
 , (19)
, (19)
где α, β, γ – координаты вектора 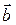 в базисе, образованном векторами
в базисе, образованном векторами 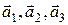 .
.
Координаты α, β, γ находятся из системы уравнений:
 . (20)
. (20)
Пример выполнения задания.
Показать, что векторы  (3; 1; 4), (3; 1; 4),  (2; 1; –1), (2; 1; –1),  (1; –1; 5) образуют базис трехмерного пространства. Найти координаты вектора (1; –1; 5) образуют базис трехмерного пространства. Найти координаты вектора  (5; 0; 3) в этом базисе. (5; 0; 3) в этом базисе.
|
|
|
Решение:
Вычислим смешанное произведение векторов 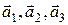 :
:
 .
.
Так как смешанное произведение отлично от нуля, то векторы некомпланарны и образуют базис. Координаты вектора  в этом базисе найдем, разложив его по векторам
в этом базисе найдем, разложив его по векторам 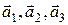 следующим образом:
следующим образом:
 ,
,
а координаты вектора  в новом базисе найдем из системы уравнений (20)
в новом базисе найдем из системы уравнений (20)
 или
или 
Решим эту систему для заданных векторов методом Гаусса.
Поменяем местами первое и второе уравнения
 .
.
После этого умножим первое уравнение на (–3) и сложим со вторым. Далее умножим первое уравнение на (–4) и сложим с третьим. Получим:
 .
.
Затем умножаем второе уравнение на (−5) и складываем с третьим:
 .
.
Из последнего уравнения имеем γ= 2. Подставляем это значение во второе уравнение, получаем β= 3 и, наконец, из первого уравнения находим α= –1.
Таким образом, подставив в уравнение (19) координаты вектора  , получим
, получим
 .
.
Задача 4.
Теоретические сведения.
Неоднородная система трех уравнений с тремя неизвестными в общем случае имеет вид

и может быть записана в матричном виде
А · Х = Н, (21)
где  - матрица коэффициентов при неизвестных,
- матрица коэффициентов при неизвестных,
 - матрица-столбец неизвестных,
- матрица-столбец неизвестных,
 матрица-столбец свободных членов.
матрица-столбец свободных членов.
Если матрица А – невырожденная, то есть имеет определитель, отличный от нуля, то существует матрица А-1, обратная к А, так что А-1·А = Е (Е - единичная матрица). Умножим обе части уравнения (22) на А-1 и получим
А-1·А·Х = А-1· Н,
или
Х = А-1· Н, (23)
поскольку А-1·А·Х = Е·Х=Х.
Равенство (23) является решением системы уравнений (22).
Матрица, обратная к невырожденной матрице А, находится по формуле
|
|
 , (24)
, (24)
где Аіј (i = 1, 2, 3; j = 1, 2, 3) – алгебраическое дополнение элемента аij, которое является произведением (-1)i+j на минор (определитель) второго порядка, полученный вычеркиваем i -й строки и j -го столбца в определителе матрицы А; Δ – определитель матрицы А.