ПРАКТИЧЕСКАЯ РАБОТА № 1
Тема: «Преобразование алгебраических, рациональных, иррациональных, степенных выражений».
Цель работы: научиться выполнять преобразование алгебраических, рациональных, иррациональных, степенных выражений с использованием формул сокращенного умножения, основных свойств корней и степеней.
Теоретические сведения.
КОРНИ НАТУРАЛЬНОЙ СТЕПЕНИ ИЗ ЧИСЛА, ИХ СВОЙСТВА.
Корень n – степени:  , n - показатель корня, а – подкоренное выражение
, n - показатель корня, а – подкоренное выражение
Если n – нечетное число, то выражение  имеет смысл при
имеет смысл при  а
а
Если n – четное число, то выражение 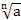 имеет смысл при
имеет смысл при 
Арифметический корень: 
Корень нечетной степени из отрицательного числа: 
ОСНОВНЫЕ СВОЙСТВА КОРНЕЙ
1. Правило извлечения корня из произведения:

2. Правило извлечения корня из дроби:

3. Правило извлечения корня из корня:

4. Правило вынесения множителя из под знака корня:
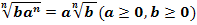
5. Внесение множителя под знак корня:
 ,
,
6. Показатель корня и показатель подкоренного выражения можно умножить на одно и тоже число.

7. Правило возведения корня в степень.
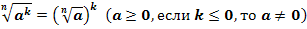
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
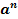 =
= 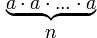 , a – основание степени, n – показатель степени
, a – основание степени, n – показатель степени
Свойства:
1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным.
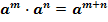
2. При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным.

3. При возведении степени в степень показатели перемножаются.

4. При возведении в степень произведения двух чисел, каждое число возводят в эту степень, а результаты перемножают.

5. Если в степень возводят частное двух чисел, то в эту степень возводят числитель и знаменатель, а результат делят друг на друга.

6. Если 
СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
1. 
2. 
3. 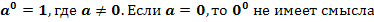
4. По определению: 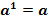

Свойства:
1. 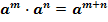
2. 
3. 
4. 
5. 
6. Пусть r рациональное число  , тогда
, тогда
 при r>0
при r>0 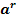 >
> 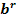 при r<0
при r<0
7. Для любого рациональных чисел r и s из неравенства  >
>  следует
следует
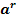 >
>  при a>1
при a>1  при
при 
Формулы сокращённого умножения.

Пример 1. Упростите выражение  .
.
Решение
Применим свойства степеней (умножение степеней с одинаковым основанием и деление степеней с одинаковым основанием):  .
.
Ответ: 9m7.
Пример 2. Сократить дробь: 
Решение.Так область определения дроби  все числа, кроме х ≠ 1 и х ≠ -2.Вместе с тем
все числа, кроме х ≠ 1 и х ≠ -2.Вместе с тем  .Сократив дробь, получим
.Сократив дробь, получим  .Область определения полученной дроби: х ≠ -2, т.е. шире, чем область определения первоначальной дроби. Поэтому дроби
.Область определения полученной дроби: х ≠ -2, т.е. шире, чем область определения первоначальной дроби. Поэтому дроби  и
и  равны при х ≠ 1 и х ≠ -2.
равны при х ≠ 1 и х ≠ -2.
Пример 3. Сократить дробь: 
Пример 4. Упростить: 
Пример 5. Упростить: 
Пример 6. Упростить: 
Пример 7. Упростить: 
Пример 8. Упростить: 
Пример 9. Вычислить:  .
.
Решение. 
Пример 10. Упростить выражение: 
Решение. 
Пример 11. Сократить дробь  , если
, если 
Решение.  .
.
Пример 12. Освободиться от иррациональности в знаменателе дроби 
Решение. В знаменателе имеем иррациональность 2-й степени, поэтому помножим и числитель, и знаменатель дроби на сопряженное выражение, то есть сумму чисел  и
и  , тогда в знаменателе будем иметь разность квадратов, которая и ликвидирует иррациональность.
, тогда в знаменателе будем иметь разность квадратов, которая и ликвидирует иррациональность. 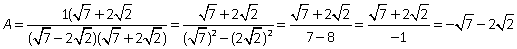
ВАРИАНТ - I
1. Упростите выражение:
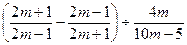 2. Найдите значение выражения:
2. Найдите значение выражения:
 3. Представьте степень с дробным показателем в виде корня
3. Представьте степень с дробным показателем в виде корня
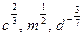 4. Привести указанное выражение к виду
4. Привести указанное выражение к виду  , где а -рациональное число, b – натуральное число , где а -рациональное число, b – натуральное число
 , , 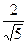 5. Упростить:
5. Упростить:
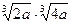 ; ;  6. Замените арифметические корни степенями с дробным показателем
6. Замените арифметические корни степенями с дробным показателем
 , ,  , ,  7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
 10. Выполните действие:
8. Сократите дробь 10. Выполните действие:
8. Сократите дробь   9. Выполните действие
9. Выполните действие 
| ВАРИАНТ - II
1. Упростите выражение:
 2. Найдите значение выражения:
2. Найдите значение выражения:
 3. Представьте степень с дробным показателем в виде корня
3. Представьте степень с дробным показателем в виде корня
 4. Привести указанное выражение к виду
4. Привести указанное выражение к виду  , где а- рациональное число, b – натуральное число , где а- рациональное число, b – натуральное число
 , , 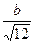 5. Упростить:
5. Упростить:
 ; ;  6. Замените арифметические корни степенями с дробным показателем
6. Замените арифметические корни степенями с дробным показателем
 , , 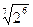 , , 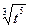 7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
 10. Выполните действие:
8. Сократите дробь 10. Выполните действие:
8. Сократите дробь   9. Выполните действие
9. Выполните действие 
|
ВАРИАНТ - III
1. Выполните действие:
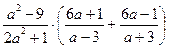 2. Найдите значение выражения:
2. Найдите значение выражения:
 3. Представьте степень с дробным показателем в виде корня
3. Представьте степень с дробным показателем в виде корня
 4. Привести указанное выражение к виду
4. Привести указанное выражение к виду  , где а -рациональное число, b – натуральное число , где а -рациональное число, b – натуральное число
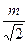 , ,  5. Упростить:
5. Упростить:
 ; ;  6. Замените арифметические корни степенями с дробным показателем
6. Замените арифметические корни степенями с дробным показателем
 , ,  , , 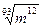 7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
 10. Выполните действие:
8. Сократите дробь 10. Выполните действие:
8. Сократите дробь 
 9. Выполните действие
9. Выполните действие

| ВАРИАНТ - IV
1. Выполните действие:
 2. Найдите значение выражения:
2. Найдите значение выражения:
 3. Представьте степень с дробным показателем в виде корня
3. Представьте степень с дробным показателем в виде корня
 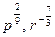 , ,  4. Привести указанное выражение к виду
4. Привести указанное выражение к виду  , где а- рациональное число, b – натуральное число , где а- рациональное число, b – натуральное число
 , , 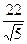 5. Упростить:
5. Упростить:
 ; ;  6. Замените арифметические корни степенями с дробным показателем
6. Замените арифметические корни степенями с дробным показателем
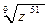 , , 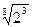 , ,  7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
 10. Выполните действие:
8. Сократите дробь 10. Выполните действие:
8. Сократите дробь 
 9. Выполните действие
9. Выполните действие

|
ВАРИАНТ - V
1. Упростите выражение:
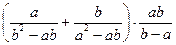 2. Найдите значение выражения:
2. Найдите значение выражения:
 3. Представьте степень с дробным показателем в виде корня
3. Представьте степень с дробным показателем в виде корня
  , ,  4. Привести указанное выражение к виду
4. Привести указанное выражение к виду  , где а- рациональное число, b – натуральное число , где а- рациональное число, b – натуральное число
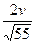 , ,  5. Упростить:
5. Упростить:
 ; ;  6. Замените арифметические корни степенями с дробным показателем
6. Замените арифметические корни степенями с дробным показателем
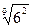 , , 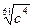 , ,  7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
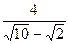 10. Выполните действие:
8. Сократите дробь 10. Выполните действие:
8. Сократите дробь 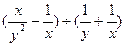
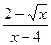 9. Выполните действие
9. Выполните действие

| ВАРИАНТ - VI
1. Упростите выражение:
 2. Найдите значение выражения:
2. Найдите значение выражения:
 3. Представьте степень с дробным показателем в виде корня
3. Представьте степень с дробным показателем в виде корня
  , ,  4. Привести указанное выражение к виду
4. Привести указанное выражение к виду  , где -а рациональное число, b – натуральное число , где -а рациональное число, b – натуральное число
 , , 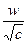 5. Упростить:
5. Упростить:
 ; ;  6. Замените арифметические корни степенями с дробным показателем
6. Замените арифметические корни степенями с дробным показателем
 , ,  , ,  7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
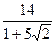 10. Выполните действие
8. Сократите дробь 10. Выполните действие
8. Сократите дробь 
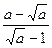 9. Выполните действие
9. Выполните действие

|