Теоретический материал
Теория
Понятие дискретной случайной величины
Дискретной случайной величиной (ДСВ) называется случайная величина ξ, имеющая дискретное распределение вероятностей, определяемое дискретным множеством значений 
и заданными вероятностями значений
ДСВ имеет следующие функциональные и числовые характеристики
• функция распределения:
• функции вероятности:
• математическое ожидание:
• дисперсия:
Алгоритм моделирования ДСВ ξ, заданной распределением (13), состоит из вычисления вспомогательного вектора 
и двух шагов, повторяющихся при каждом обращении к алгоритму:
1. Моделирование с помощью датчика БСВ реализации a.
2. Принятие решения о том, что реализацией ξ является x, определяемое по правилу:
Алгоритмы моделирования для дискретных распределений
На практике для описания ДСВ используются модельные дискретные законы распределения с числом параметров N'<<N. Это позволяет построить более экономичные и точные алгоритмы моделирования ДСВ.
Распределение Бернулли
ДСВ ξ имеет распределение Бернулли Bi(1,p), если 
, 
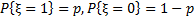, где 
- параметр распределения.
Характеристики распределения Bi(1,p) (x ε{0,1}):
Распределение Бернулли описывает случайный эксперимент (испытание Бернулли) с двумя исходами: успех (ξ = 1) и неудача (ξ = 0), причем вероятность успеха равна p.
Алгоритм моделирования одной реализации случайной величины Бернулли состоит из двух шагов:
1. Моделирование реализации БСВ.
2. Принятие решения о том, что реализацией ξ является значение x определяемое по правилу:
Коэффициент использования БСВ k = 1.
Точечная оценка параметра распределения Бернулли.
Пусть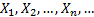 
– случайная выборка для распределения, зависящего от параметра 
. Тогда статистику 
, принимающую значения в 
, называют точечной оценкой параметра 
.
В качестве точечной оценки параметра распределения Бернулли 
можно взять значение 
, где 
– реализация случайной величины, которая имеет распределение Бернулли.
Доверительный интервал для параметра распределения Бернулли.
Доверительным интервалом параметра распределения СВ 
с уровнем доверия 
, порожденным выборкой 
, называется интервал с границами 
и 
, которые являются реализациями случайных величин 
и 
, таких, что 
.
Формулы для искомого доверительного интервала параметра распределения Бернулли, т.е. такие 
и 
, что 
:
Дискретное равномерное распределение
ДСВ ξ имеет дискретное равномерноераспределение, если она принимает конечное число значений с равными вероятностями.
Параметры распределения: a, b – целые числа.
Характеристики распределения:
· функция распределения:
· функция вероятности:
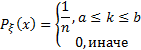
· математическое ожидание
· дисперсия
Биномиальное распределение
ДСВ ξ имеет биномиальное распределение Bi(m,p), если: 
.
Параметры распределения: m – натуральное число; p ε (0,1).
Характеристики распределения Bi(m,p) (x ε {0,1,…,m}):
Биномиальная СВ ξ – это число успехов в m независимых испытаниях Бернулли, если вероятность успеха в каждом испытании равна p.
Алгоритм моделирования реализации биноминальной СВ ξ по методу браковки состоит из двух шагов:
1. Моделирование m реализаций БСВ
2. Принятие решения о том, что реализацией ξ является значение x, вычисляемое по формуле:
Таким образом, x – количество значений из { ai }, меньших p.
Коэффициент использования БСВ k = 1/m.