Задание 16
| Определение | Скалярная величина - величина, которая может быть охарактеризована числом. Например, длина, площадь, масса, температура и т.д.
Вектором называется направленный отрезок  ; точка ; точка  - начало, точка - начало, точка  - конец вектора (рис. 1). - конец вектора (рис. 1).
|

Вектор обозначается либо двумя большими буквами - своим началом и концом:  либо одной малой буквой:
либо одной малой буквой:  .
.
| Определение | Если начало и конец вектора совпадают, то такой вектор называется нулевым. Чаще всего нулевой вектор обозначается как 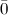 .
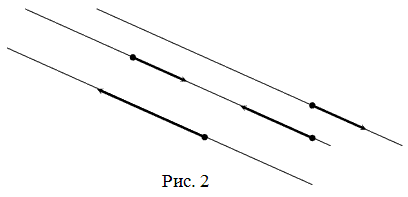
Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 2). .
Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 2).
|
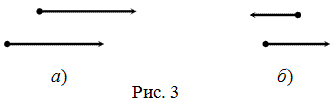
| Определение | Два коллинеарных вектора  и и  называются сонаправленными, если их направления совпадают: называются сонаправленными, если их направления совпадают:  (рис. 3, а). Два коллинеарных вектора (рис. 3, а). Два коллинеарных вектора  и и  называются противоположно направленными, если их направления противоположны: называются противоположно направленными, если их направления противоположны: 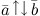 (рис. 3, б). (рис. 3, б).
|
| Определение | Векторы называются компланарными, если они параллельны одной плоскости или лежат в одной плоскости (рис. 4). |

Два вектора всегда компланарны.
· ДЛИНА (МОДУЛЬ) ВЕКТОРА
| Определение | Длиной (модулем) вектора  называется расстояние между его началом и концом: называется расстояние между его началом и концом: 
|
Длина нулевого вектора 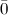 равна нулю. Длина единичного вектора
равна нулю. Длина единичного вектора  равна единице.
равна единице.
Если вектор задан своими координатами: 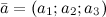 , то его длина находится по формуле:
, то его длина находится по формуле:
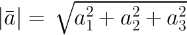
*здесь указаны a1, a2, a3, а 2 вверху в формуле означает, что эти числа взяты в квадрат
| Определение | Вектор, длина которого равна единице, называется единичным вектором или ортом.
Векторы называются равными, если они лежат на одной или параллельных прямых; их направления совпадают и длины равны.
Иначе говоря, два вектора равны, если они коллинеарны, сонаправлены и имеют равные длины:
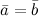 , если , если 
|
В произвольной точке  пространства можно построить единственный вектор
пространства можно построить единственный вектор  , равный заданному вектору
, равный заданному вектору  .
.
| Определение | Длина вектора, заданного координатами, равна корню квадратному из суммы квадратов его координат. |
| Пример | Задание. Найти длину  Решение. Используя формулу, получаем:
Решение. Используя формулу, получаем:

|
· ОПЕРАЦИИ НАД ВЕКТОРАМИ
| Определение | Линейными операциями над векторами называются операции сложения векторов и умножения вектора на число. |
· СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
| Определение | Сложение векторов  и и  осуществляется по правилу треугольника.
Суммой осуществляется по правилу треугольника.
Суммой  двух векторов двух векторов  и и  называют такой третий вектор называют такой третий вектор  , начало которого совпадает с началом , начало которого совпадает с началом  , а конец - с концом , а конец - с концом  при условии, что конец вектора при условии, что конец вектора  и начало вектора и начало вектора  совпадают (рис. 1). совпадают (рис. 1).
|

| Определение | Правило параллелограмма - если два неколлинеарных вектора  и и  привести к общему началу, то вектор привести к общему началу, то вектор  совпадает с диагональю параллелограмма, построенного на векторах совпадает с диагональю параллелограмма, построенного на векторах  и и  (рис. 2). Причем начало вектора (рис. 2). Причем начало вектора  совпадает с началом заданных векторов. совпадает с началом заданных векторов.
|
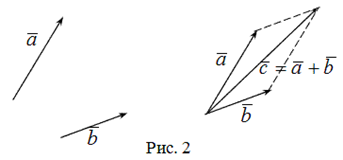
| Определение | Вектор  называется противоположным вектором к вектору называется противоположным вектором к вектору  , если он коллинеарен вектору , если он коллинеарен вектору  , равен ему по длине, но направлен в противоположную сторону вектору , равен ему по длине, но направлен в противоположную сторону вектору  . .
|
Операция сложения векторов обладает следующими свойствами:
1.  - коммутативность
- коммутативность
2.  - ассоциативность
- ассоциативность
3. 
4. 
| Определение | Разностью 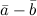 векторов векторов  и и  называется вектор называется вектор  такой, что выполняется условие: такой, что выполняется условие:  (рис. 3). (рис. 3).
|
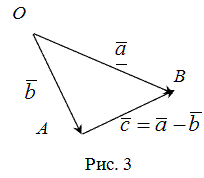
· УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
| Определение | Произведением  вектора вектора  на число на число  называется вектор называется вектор  , удовлетворяющий условиям:
1. , удовлетворяющий условиям:
1.  2.
2. 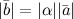 3.
3.  , если , если  , , 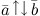 , если , если  . .
|
Свойства умножения вектора на число:
1. 
2. 
3. 
4. 
5. 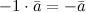
6. 
Здесь  и
и  - произвольные векторы,
- произвольные векторы,  ,
, 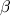 - произвольные числа.
- произвольные числа.
· РАЗЛОЖЕНИЕ ВЕКТОРА НА СОСТАВЛЯЮЩИЕ
Для двух коллинеарных векторов  и
и  всегда имеет место соотношение:
всегда имеет место соотношение:  , где
, где  - некоторое ненулевое число.
- некоторое ненулевое число.
Если ввести в рассмотрение единичный вектор (или орт)  , длина которого равна единице:
, длина которого равна единице:  и который коллинеарен вектору
и который коллинеарен вектору  , то последний можно представить в виде:
, то последний можно представить в виде: 
Произвольный вектор  можно представить в виде:
можно представить в виде:  , где
, где  ,
,  - произвольные числа, а тройка векторов
- произвольные числа, а тройка векторов  ,
,  и
и  компланарна (рис. 1).
компланарна (рис. 1).

| Определение | Представление  называется разложением вектора называется разложением вектора  по компонентам по компонентам  и и  . Если векторы . Если векторы  и и  не коллинеарны, то приведенное представление единственно. не коллинеарны, то приведенное представление единственно.
|
Для трех попарно неколлинеарных векторов  ,
,  и
и  и произвольного вектора
и произвольного вектора  существует единственное разложение:
существует единственное разложение: 
· ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ
Пусть задан вектор  и некоторая ось
и некоторая ось  с единичным вектором
с единичным вектором  . Точки
. Точки 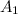 и
и  - проекции точек
- проекции точек  и
и  на ось
на ось  соответственно.
соответственно.
| Определение | Проекцией вектора  на ось на ось  называется длина отрезка называется длина отрезка  , взятая со знаком "+", если направление , взятая со знаком "+", если направление  совпадает с направлением вектора совпадает с направлением вектора  , и со знаком "-", если направление , и со знаком "-", если направление  противоположно направлению единичного вектора оси противоположно направлению единичного вектора оси  (рис. 1). (рис. 1).
|

Проекция вектора  на ось
на ось  обозначается символом
обозначается символом  .
.
· СВОЙСТВА ПРОЕКЦИИ ВЕКТОРОВ
Проекции равных векторов на одну и туже ось равны.
Вектор  и его проекция - вектор
и его проекция - вектор  - связаны следующим векторным равенством:
- связаны следующим векторным равенством:
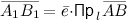
Проекция вектора  на некоторую ось
на некоторую ось  равна проекции на эту же ось вектора
равна проекции на эту же ось вектора  , умноженного на число
, умноженного на число  :
:

Проекция вектора  на ось
на ось  равна произведению модуля этого вектора на косинус угла между ним и положительным направлением оси на некоторую ось
равна произведению модуля этого вектора на косинус угла между ним и положительным направлением оси на некоторую ось  :
:

· ПРАВАЯ И ЛЕВАЯ ТРОЙКИ ВЕКТОРОВ
| Определение | Три некомпланарных вектора  , ,  и и  , приведенных к общему началу, образуют так называемую связку трех векторов (или тройку векторов).
Тройка векторов называется упорядоченной, если четко сказано, какой вектор в ней идет первым, и так далее.
Тройка векторов , приведенных к общему началу, образуют так называемую связку трех векторов (или тройку векторов).
Тройка векторов называется упорядоченной, если четко сказано, какой вектор в ней идет первым, и так далее.
Тройка векторов  , ,  и и  называется левой, если поворот от вектора называется левой, если поворот от вектора  к вектору к вектору  , видимый с конца третьего вектора , видимый с конца третьего вектора  , осуществляется по ходу часовой стрелки (рис. 1).
Тройка векторов , осуществляется по ходу часовой стрелки (рис. 1).
Тройка векторов  , ,  и и  называется правой, если поворот от вектора называется правой, если поворот от вектора  к вектору к вектору  , видимый с конца третьего вектора , видимый с конца третьего вектора  , осуществляется против хода часовой стрелки (рис. 2). , осуществляется против хода часовой стрелки (рис. 2).
|

· КООРДИНАТЫВЕКТОРА
Пусть задана прямоугольная декартова система координат (ПДСК)  и произвольный вектор
и произвольный вектор  , начало которого совпадает с началом системы координат (рис. 1).
, начало которого совпадает с началом системы координат (рис. 1).

| Определение | Координатами вектора  называются проекции называются проекции  и и  данного вектора на оси данного вектора на оси  и и 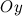 соответственно: соответственно:
 Величина
Величина  называется абсциссой вектора называется абсциссой вектора  , а число , а число  - его ординатой. То, что вектор - его ординатой. То, что вектор  имеет координаты имеет координаты  и и  , записывается следующим образом: , записывается следующим образом:  . .
|
| Пример | Запись  означает, что вектор означает, что вектор  имеет следующие координаты: абсцисса равна 5, ордината равна -2. имеет следующие координаты: абсцисса равна 5, ордината равна -2.
|
· СУММА ДВУХ ВЕКТОРОВ, ЗАДАННЫХ КООРДИНАТАМИ
Пусть заданы  и
и  , тогда вектор
, тогда вектор  имеет координаты
имеет координаты  (рис. 2).
(рис. 2).

| Определение | Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты. |
| Пример | Задание. Заданы 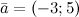 и и 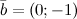 . Найти координаты вектора . Найти координаты вектора  Решение.
Решение. 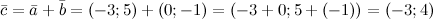
|
· УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
Если задан  , то тогда вектор
, то тогда вектор  имеет координаты
имеет координаты  , здесь
, здесь  - некоторое число (рис. 3).
- некоторое число (рис. 3).

| Определение | Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное число. |
| Пример | Задание. Вектор  . Найти координаты вектора . Найти координаты вектора 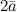 Решение.
Решение. 
|
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две точки  и
и  . Тогда координаты вектора
. Тогда координаты вектора  находятся по формулам (рис. 4):
находятся по формулам (рис. 4):

| Определение | Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат конца отнять соответствующие координаты начала. |

| Пример | Задание. Найти координаты вектора  , если , если  Решение.
Решение. 
|
· НАПРАВЛЯЮЩИЕ КОСИНУСЫ
| Определение | Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат. |
Направление вектора однозначно задается направляющими косинусами. Для единичного вектора направляющие косинусы равны его координатам.
Если в пространстве задан вектор 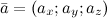 , то его направляющие косинусы вычисляются по формулам:
, то его направляющие косинусы вычисляются по формулам:

Здесь  ,
, 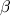 и
и  - углы, которые составляет вектор с положительными направлениями осей
- углы, которые составляет вектор с положительными направлениями осей  ,
, 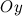 и
и  соответственно.
соответственно.
· ОСНОВНОЕ СВОЙСТВО НАПРАВЛЯЮЩИХ КОСИНУСОВ
| Определение | Сумма квадратов направляющих косинусов равна единице. |

Если известны направляющие косинусы вектора  , то его координаты могут быть найдены по формулам:
, то его координаты могут быть найдены по формулам:
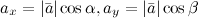
Аналогичные формулы имеют место и в трехмерном случае - если известны направляющие косинусы вектора 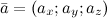 , то его координаты могут быть найдены по формулам:
, то его координаты могут быть найдены по формулам:
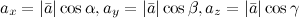
· УГОЛ МЕЖДУ ВЕКТОРАМИ
Пусть заданы два произвольных ненулевых вектора  и
и  . Приведем их к общему началу, для этого отложим от некоторой точки
. Приведем их к общему началу, для этого отложим от некоторой точки  векторы
векторы  и
и  , равные соответственно заданным векторам
, равные соответственно заданным векторам  и
и  (рис. 1).
(рис. 1).

| Определение | Углом между векторами  и и  называется угол называется угол  . .
|
Угол между сонаправленными векторами равен 0°, а между противоположно направленными - 180°.
| Определение | Два вектора называются перпендикулярными или ортогональными, если угол между ними равен 90°. |
Угол между двумя векторами 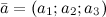 ,
, 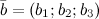 заданными своими координатами, вычисляется по формуле:
заданными своими координатами, вычисляется по формуле:
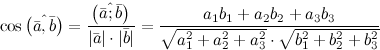
| Пример | Задание. Известно, что скалярное произведение двух векторов  , а их длины , а их длины  . Найти угол между векторами . Найти угол между векторами  и и  .
Решение. Косинус искомого угла: .
Решение. Косинус искомого угла:

|
| Пример | Задание. Найти угол между векторами  и и  Решение. Косинус искомого угла:
Решение. Косинус искомого угла:

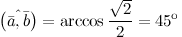
|
· РАЗЛОЖЕНИЕ ВЕКТОРА ПО ОРТАМ КООРДИНАТНЫХ ОСЕЙ
| Определение | Система ортов (или базисная система векторов) - это система единичных векторов осей координат. |
Орт координатной оси  обозначается через
обозначается через  , оси
, оси 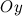 - через
- через  , оси
, оси  - через
- через 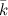 (рис. 1).
(рис. 1).

Для любого вектора  , который лежит в плоскости
, который лежит в плоскости  , имеет место следующее разложение:
, имеет место следующее разложение: 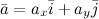
Если вектор 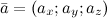 расположен в пространстве, то разложение по ортам координатных осей имеет вид:
расположен в пространстве, то разложение по ортам координатных осей имеет вид: 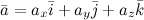
| Пример | Задание. Зная разложение  по базисной системе векторов: по базисной системе векторов:  , записать координаты этого вектора в пространстве.
Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что , записать координаты этого вектора в пространстве.
Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что  , получаем, что , получаем, что 
|
| Пример | Задание. Вектор  задан своими координатами: задан своими координатами: 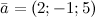 . Записать разложение данного вектора по ортам осей координат.
Решение. Координаты вектора — это коэффициенты при ортах координатных осей в разложении вектора по базисной системе, поэтому искомое разложение: . Записать разложение данного вектора по ортам осей координат.
Решение. Координаты вектора — это коэффициенты при ортах координатных осей в разложении вектора по базисной системе, поэтому искомое разложение:

|