Пространственная задача теплопроводности.
Распространение тепла в шаре
Решение задачи теплопроводности в пространстве двух и трех измерений связано с большими трудностями математического характера. Возможности использования математического аппарата в настоящем курсе сильно ограничены. Поэтому рассмотрим краевую задачу для трехмерного пространства, решение которой можно привести к одномерному случаю.
Пусть имеем однородный шар радиуса 
, центр которого находится в начале координат. Предположим, что как в начальный, так и в последующие моменты времени температура одна и та же во всех точках, находящихся на одинаковой расстоянии 
от центра шара. Во все время наблюдения внешняя поверхность шара поддерживается при нулевой температуре. Определим температуру любой точки внутри сферы в момент времени 
.
Преобразуем уравнение теплопроводности в пространстве трех координат
| (1.250) |
к уравнению с одной пространственной координатой, т.к. температура 
в точке 
для по условию зависит от ее расстояния до начала координат.
Значит,
 , где  .
| (1.251) |
Из (1.250) найдем
,
.
Аналогично определяются 
, 
. После подстановки в (1.250) найденных выражений для частных производных 
, , уравнение примет вид
 .
| (1.252) |
Тогда начальное условие запишется в виде
 ,
| (1.253) |
где 
- заданная функция в интервале 
, а граничное условие
 .
| (1.254) |
Если ввести новую неизвестную функцию
 ,
| (1.255) |
то задача легко сводится к решенной ранее одномерной краевой задаче с однородными граничными условиями. В самом деле, из (1.255) найдем
, 
, 
.
Выразим отсюда 
, 
, 
и подставим их значения в (1.252). Уравнение (1.252) преобразуется к виду
,
а условия для новой функции 
таковы:
,
, 
.
В результате мы пришли к задаче о теплопроводности в конечном стержне длины , на концах которого поддерживается температура, равная нулю, а начальное распределение температуры задается функцией 
. Эта задача решена в п. 1.33.1А. Согласно формулам (1.202) и (3.203) имеем
,
где
.
Искомая же температура 
.
Уравнения эллиптического.
Задачи, приводящие к уравнениям Пуассона и Лапласа
Исследование стационарных процессов различной физической природы приводит к уравнениям эллиптического типа. Простейшими и наиболее распространенными уравнениями этого типа являются уравнения Пуассона и Лапласа.
К уравнениям Пуассона и Лапласа, помимо задачи о распределении температуры в стационарном тепловом поле, что было установлено в п. 1.31, приводятся многие задачи из электростатики, магнитостатики, гидродинамики и других разделов естествознания. Остановимся на некоторых из них.
Основное уравнение электростатики
Пусть в некоторой однородной среде имеется стационарное, т.е. не зависящее от времени, электрическое поле, образованное электрическими зарядами. 
- напряженность электрического поля; 
- плотность зарядов; диэлектрическую постоянную среды примем равной единице.
Основным законом электростатического поля является теорема Гаусса: поток напряженности через произвольную замкнутую поверхность 
равен (в абсолютной системе единиц) алгебраической сумме зарядов, находящихся внутри этой поверхности, умноженной на 
:
.
В общем случае электрические заряды распределены по объему 
с некоторой плотностью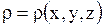 
. Заряд 
, помещенный в элементе объема 
, можно рассматривать как точечный заряд, а данное электрическое поле напряженности - как поле, образованное наложением точечных зарядов. Поэтому сумма 
должна быть заменена на 
. Итак, в силу основного закона
 .
| (1.256) |
Применив к поверхностному интегралу формулу Остроградского-Гаусса
,
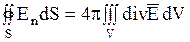из (1.256) получаем
или
.
Отсюда, ввиду произвольности объема , следует, что равно нулю подынтегральное выражение. Таким образом, перешли к дифференциальной форме теоремы Гаусса
 .
| (1.257) |
Из электродинамики известно, что электростатическое поле является безвихревым, или потенциальным, т.е. существует такая скалярная функция 
, для которой
,
где 
- электрический потенциал.
В векторном анализе было установлено, что
.
С учетом этого уравнение (1.257) примет вид
 .
| (1.258) |
В системе единиц СИ уравнение (1.258) записывается проще:
.
Отсюда заключаем, что потенциал электрического поля удовлетворяет уравнению Пуассона. Если объемных зарядов нет 
, то потенциал удовлетворяет уравнению Лапласа:
.