Свойства функций непрерывных в точке.

Непрерывность функции.

1.Непрерывность функции в точке.

Свойства функций непрерывных в точке.

2.Односторонние пределы, односторонняя непрерывность.

3.Точки разрыва функции и их классификация.

4. Свойства функций непрерывных на отрезке.

Введение.

Наше представление о непрерывности функции обычно связано с изображением этой функции в виде графика, причём функцию мы считаем непрерывной, если её график представляет собой сплошную, непрерывную линию. Однако такое представление о непрерывной функции даёт только наглядный смысл понятия непрерывности; определением непрерывной функции это служить не может, так как здесь мы ссылаемся на другое, ещё не определённое понятие – понятие непрерывности линии

Для того чтобы изучить свойства непрерывных функций, необходимо иметь четкое определение непрерывности. Это определение должно быть, во-первых, математически строгим (т.е. опираться на ранее введённые понятия) и, во-вторых, согласовываться с тем наглядным, интуитивным представлением о непрерывной функции, которое дано нам практикой, опытом.

Непрерывность функции в точке.

Свойства функций непрерывных в точке.

Понятие непрерывности функции является одним из основных понятий математического анализа.

Определение1. Функция называется непрерывной в точке , если предел функции и её значение в этой точке равны, т.е. (1)

Из определения следует, что если функция непрерывна в точке , то она определена в этой точке, т.е. существует . Так как, то соотношение (1) можно записать в виде

,

т.е. для непрерывной функции можно менять местами знак функции и знак предела.

Определение2. (на языке последовательностей). Функция называется непрерывной в точке , если для любой последовательности значений аргумента сходящейся к , последовательность соответствующих значений функции: сходящейся к .

Определение3. (''на языке ''). Функция называется непрерывной в точке , если для любого E>0 существует такое, что для всех x удовлетворяющих неравенству , выполняется неравенство .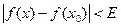

Эквивалентность этих определений очевидна.

Перенесем в равенстве (1) в левую часть и внесём под знак предела. Так как условия и равносильны, то получаем

(2)

Разность называется приращением аргумента x в точке и обозначается , а разность - приращением функции в точке и обозначается . Таким образом, , .

У

f (x₀+∆x) y=f(x)

∆y

f(x₀)

∆x

0 x₀ x₀+∆x x

Равенство (2) в новых обозначениях примет вид

(3)

Соотношение (3) является ещё одним определением непрерывности функции в точке.

Определение4. Функция называется непрерывной если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Теорема1. Все основные элементарные функции непрерывны в каждой точке своей области определения.

Теорема2. Пусть функции и непрерывны Тогда функции также непрерывны в точке (последняя при условии, что ).

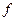Теорема3. Если и функция непрерывна в точке 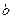, то , или .

Теорема4. Пусть функция непрерывна а функция непрерывна в точке . Тогда сложенная функция непрерывна в точке .