Построение ковариационной матрицы для исследуемого множества объектов

ОТЧЕТ ПО ИНДИВИДУАЛЬНОМУ ДОМАШНЕМУ ЗАДАНИЮ

По дисциплине: Планирование эксперимента

На тему: Снижение размерности пространства признаков.

Метод главных компонент.

Вариант 2

Выполнила:Антонович М.В.

Преподаватель:Манило Л.А.

Санкт-Петербург

СПбГЭТУ «ЛЭТИ»

Содержание

Введение. 3

Расчёты.. 4

1. Преобразование матрицы наблюдений путем центрирования исходных признаков ........................ 6

2. Построение ковариационной матрицы для исследуемого множества объектов 12

3. Набор собственных векторов матрицы ковариаций. 13

4. Переход от исходных центрированных признаков к главным компонентам 16

5. Определение новых координат объектов: .......................... 16

6. Построение кривой изменения относительной доли суммарной дисперсии, обусловленной первыми компонентами 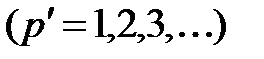........................ 16

7. Оценка доли дисперсии, которая обеспечивается первыми двумя главными компонентами 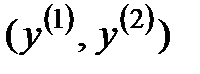.............. 17

8. Отображение распределения объектов заданных классов в пространстве новых признаков ............... 18

Вывод. 19

Введение

Цель работы: освоение метода главных компонент с помощью программной среды MathCad.

Исходные данные: результат описания множества реализаций ЭКГ набором признаков ApEn (1), ApEn (2), ApEn (3), ApEn (4), ApEn (5), ME.

Эти признаки получены в процессе вычисления и анализа параметров энтропии Колмогорова, которая отражает степень сложности ритмограммы.

Выборка данных включает несколько классов ЭКГ:

МА – мерцательная аритмия,

НР – нормальный ритм,

ЧЭ – частая экстрасистолия.

Каждый из классов представлен 25 объектами.

Задание:

Требуется для всей совокупности данных, используя метод главных компонент, выполнить следующие преобразования:

1) преобразовать матрицы наблюдений путем центрирования исходных признаков ;

2) построить ковариационную матрицу для исследуемого множества объектов;

3) найти набор собственных векторов матрицы ковариаций;

4) осуществить переход от исходных центрированных признаков к главным компонентам;

5) определить новые координаты объектов: ;

6) построить кривую изменения относительной доли суммарной дисперсии, обусловленной первыми компонентами ;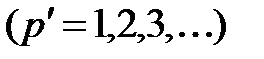

7) оценить долю дисперсии, которая обеспечивается первыми двумя главными компонентами ;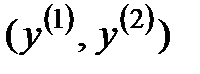

8) отобразить распределение объектов заданных классов в пространстве новых признаков: или .

Расчёты

Имеетсявыборка данных (файл Вар_2.xls), состоящая из двух классов, где каждый класс представлен 25-ю объектами:

1) МА– мерцательная аритмия

Таблица 1.Мерцательная аритмия

№	ApEn(1)	ApEn(2)	ApEn(3)	ApEn(4)	ME
	1,887	1,203	0,372	0,069	0,672
	1,897	1,126	0,363	0,130	0,794
	1,902	1,222	0,347	0,050	0,723
	1,962	1,074	0,342	0,066	0,873
	1,999	1,133	0,244	0,051	0,842
	2,018	1,114	0,245	0,028	0,907
	1,984	1,165	0,260	0,048	0,798
	2,022	1,064	0,294	0,050	0,878
	1,941	1,148	0,364	0,063	0,760
	1,929	1,196	0,328	0,049	0,705
	1,968	1,171	0,316	0,077	0,728
	1,922	1,141	0,376	0,069	0,739
	1,992	1,086	0,321	0,028	0,835
	1,961	1,193	0,290	0,033	0,734
	1,915	1,214	0,360	0,047	0,734
	1,869	1,231	0,421	0,069	0,614
	1,969	1,175	0,296	0,059	0,833
	1,884	1,162	0,423	0,089	0,765
	1,902	1,202	0,386	0,074	0,649
	1,943	1,141	0,336	0,059	0,803
	1,893	1,219	0,405	0,048	0,634
	1,839	1,170	0,456	0,123	0,723
	1,858	1,243	0,405	0,072	0,686
	1,920	1,215	0,341	0,020	0,832
	1,985	1,169	0,300	0,062	0,763

2) НР – нормальный ритм

Таблица 2. Нормальный ритм

№	ApEn(1)	ApEn(2)	ApEn(3)	ApEn(4)	ME
	1,434	1,128	0,553	0,152	1,027
	1,480	1,196	0,670	0,193	0,847
	1,307	1,057	0,697	0,384	1,022
	1,235	1,016	0,702	0,391	0,984
	1,345	1,070	0,729	0,404	0,911
	1,265	0,988	0,708	0,428	1,003
	1,201	0,911	0,696	0,455	1,048
	1,228	0,995	0,777	0,470	0,750
	1,840	0,977	0,279	0,029	1,081
	1,806	0,903	0,189	0,031	1,317
	1,040	0,912	0,680	0,487	1,179
	1,875	0,876	0,218	0,029	1,394
	1,078	0,937	0,697	0,431	1,203
	1,058	0,906	0,716	0,474	1,143
	1,140	0,956	0,683	0,413	1,040
	1,975	0,841	0,158	0,020	1,354
	1,232	0,925	0,579	0,279	1,347
	1,339	0,884	0,452	0,183	1,606
	1,295	0,995	0,577	0,222	1,312
	1,465	0,885	0,472	0,157	1,397
	0,808	0,603	0,497	0,396	1,305
	1,449	1,165	0,678	0,290	0,832
	1,315	0,902	0,460	0,219	1,609
	1,444	1,045	0,612	0,256	1,065
	1,245	1,012	0,663	0,366	1,116

1. Преобразование матрицы наблюдений путем центрирования исходных признаков

Выполним импорт данных из Excelв Mathcad, проделав следующие операции:

1) Вставка → Данные → Ввод из файла…

2) Задаём путь к файлу, выбираем нужный нам лист и диапазон ячеек.

Получим:

Центрирование производится по следующей формуле:

,где

Для получения матрицы исходных данных произведём объединение двух классов:

Таблица 3. Матрица исходных данных

Отобразим полученную таблицу с помощью оператора ORIGIN.

Таблица 4. Матрица исходных данныхс оператором ORIGIN

Рисунок 2 – График распределения исходных признаков

Вычислим средние значения столбцов:

Выполним центрирование признаков:

Построение ковариационной матрицы для исследуемого множества объектов

Ковариационная матрица вычисляется по следующей формуле:

Пример расчёта элемента ковариационной матрицы:

,

где 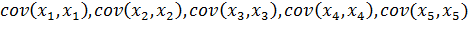– дисперсии.

Вычислим ковариационную матрицу:

Построение ковариационной матрицы для исследуемого множества объектов

Поиск по сайту