Задачи для подготовки к зачету
Задача 1. Уравнение регрессии в стандартизированном виде имеет вид:


Определите частные коэффициенты эластичности.
Задача 2. По 18 наблюдениям получены следующие данные:
 ,
,  ;
;  ;
;  ;
;  ;
;  . Определите значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра а.
. Определите значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра а.
Задача 3. Уравнение регрессии в стандартизованном виде имеет вид: 

Как влияют факторы на результат и каковы значения частных коэффициентов эластичности?
Задача 4. По следующим данным: 





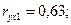

 , запишите уравнения регрессии y на x1 и x2 в стандартизованном и натуральном масштабе.
, запишите уравнения регрессии y на x1 и x2 в стандартизованном и натуральном масштабе.
Задача 5. При построении регрессионной зависимости некоторого результативного признака на 8 факторов по 25 измерениям коэффициент детерминации составил 0,736. После исключения 3 факторов коэффициент детерминации уменьшился до 0,584. Обоснованно ли было принятое решение на уровнях значимости 0,1, 0,05 и 0,01?
Задача 6. По данным 150 наблюдений о доходе индивидуума Y, уровне его образования X1, и возрасте X2 определите, можно ли считать на уровне значимости 5 % линейную регрессионную модель Y на X1 и X2 гетероскедастичной, если суммы квадратов остатков после упорядочения данных по уровню образования следующие RSS1 (для 50 значений с наименьшим уровнем образования) = 894,1; RSS2 (для 50 значений с наибольшим уровнем образования) = 3918,2.
Задача 7. При построении регрессионной зависимости  по 40 измерениям коэффициент детерминации составил 0,618. После исключения факторов x4 и x5 коэффициент детерминации уменьшился до 0,547. Обоснованно ли было принятое решение на уровнях значимости 0,1; 0,05 и 0,01?
по 40 измерениям коэффициент детерминации составил 0,618. После исключения факторов x4 и x5 коэффициент детерминации уменьшился до 0,547. Обоснованно ли было принятое решение на уровнях значимости 0,1; 0,05 и 0,01?
Задача 8. При анализе данных на гетероскедастичность вся выборка была после упорядочения разбита на три подвыборки. Затем по результатам парных регрессий остаточная СКО в первой подвыборке составила 6450, в третьей – 3480. Подтверждается ли наличие гетероскедастичности на уровнях 0,1; 0,05 и 0,01, если объем данных в каждой подвыборке равен 25?
Задача 9. Уравнение регрессии, построенное по 12 наблюдениям, имеет вид:
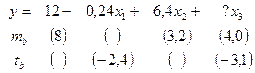
Определите пропущенные значения и доверительный интервал для  с вероятностью 0,99.
с вероятностью 0,99.
Задачи для домашней работы
Задача 1. Коэффициенты корреляции между переменными y, x1, x2 равны: ryx1= 0,8; ryx2= 0,7; rx1x2=0,9. Задание: определить коэффициент множественной корреляции между переменной y и переменными x1, x2?
Задача 2. По 30 заводам, выпускающим продукцию А, изучается зависимость потребления электроэнергии y (тыс. кВт*ч) от производства продукции – x1(тыс. ед.) и уровня механизации труда – x2(%). Данные приведены в таблице:
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| y | ryx1=0,77 | ||
| x1 | ryx2=0,43 | ||
| x2 | 41,5 | rx1x2=0,38 |
Задание: построить уравнение множественной регрессии в стандартизованной и натуральной форме; определить показатели частной и множественной корреляции; найти частные коэффициенты эластичности и сравнить их с β-коэффициентами.
Задача 3. На основе статистических данных за 10 лет оценены параметры и их стандартные ошибки для линейной модели, описывающей зависимость объемов производства y от количества работающих x1 и установочной мощности оборудования x2:

(6,5) (5,1) (0,83)
Задание: установить для уровня значимости  0,05, оказывают ли объясняющие переменные x1, x2 существенное влияние на объясняемую переменную y.
0,05, оказывают ли объясняющие переменные x1, x2 существенное влияние на объясняемую переменную y.
Задача 4. Имеются данные регрессионного анализа чистого дохода в зависимости от стоимости капитала и численности служащих по 20 предприятиям (табл.6.3):
| Множественный R | ? | |||
| R-квадрат | ? | |||
| Нормированный R-квадрат | ? | |||
| Стандартная ошибка | 1,249 | |||
| Наблюдения | ||||
| df | SS | MS | F | |
| Регрессия | ? | 30,821 | ? | ? |
| Остаток | ? | 26,537 | ? | |
| Итого | ? | 57,358 | ||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | 1,706 | 0,463 | ? | 0,002 |
| X1 | 0,072 | 0,016 | ? | 0,0003 |
| X2 | -0,002 | 0,002 | ? | 0,202 |
Задание:
1) записать линейное уравнение множественной регрессии и пояснить экономический смысл его параметров;
2) оценить качество уравнения и проверить значимость коэффициентов регрессии и R2 при α=0,05.
Задача 5. Имеются данные регрессионного анализа цен на туристические палатки. Уравнение регрессии имеет следующий вид: Цена=120+73,2*(вес)-7,52*(площадь):
| Независимая переменная | Коэффициент | Стандартная ошибка | t-статистика | p |
| Константа | 120,3 | 54,82 | 2,19 | 0,037 |
| Вес | 73,17 | 15,37 | 4,76 | 0,000 |
| Площадь | -7,517 | 2,546 | -2,95 | 0,006 |
R2=0,567, R2скорр.=0,535, n=30.
Задание: ответить на ряд вопросов:
1) стоят ли более тяжелые палатки в среднем дороже или дешевле, чем легкие, если речь идет о палатках заданного размера?
2) стоят ли большие палатки в среднем дороже или дешевле, чем меньшие палатки, если речь идет о палатках заданного веса?
3) какой процент вариации цен объясняется информацией, доступной руководству компании?
4) найдите цену палатки, вес которой составит 5 кг, а площадь 4 квадратных метра;
5) является ли значимым F-критерий?
Задача 6. По 30 территориям России имеются следующие данные:
| Признак | Среднее значение | Среднее квадратическое отклонение | Линейные коэффициенты парной корреляции |
Среднедневной душевой доход 
| 86,8 | 11,44 | 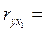 0,8405 0,8405
 -0,2101 -0,2101
 -0,1160 -0,1160
|
Среднедневная зарплата 
| 54,9 | 5,86 | |
Средний возраст безработного 
| 33,5 | 0,58 |
Задание:
1) построить уравнение множественной регрессии в стандартизованной и естественной форме, рассчитать частные коэффициенты эластичности и сравнить их со стандартизованными коэффициентами регрессии.
2) рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции и сравнить их с коэффициентами парной корреляции.
3) рассчитать общий и частные  критерии Фишера.
критерии Фишера.
Задача 7. По ряду регионов множественная регрессия величины импорта y на определенный товар относительно отечественного его производства x1, изменения запасов x2 и потребления на внутреннем рынке x3 оказалась следующей
 .
.
При этом  31,5;
31,5;  245,7;
245,7;  3,7;
3,7;  182,5.
182,5.
Задание: определить параметр 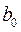 , частные уравнения регрессии и частные коэффициенты эластичности для региона с показателями
, частные уравнения регрессии и частные коэффициенты эластичности для региона с показателями  160,2;
160,2;  4,0;
4,0; 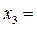 190,5.
190,5.