В ЭВМ операция умножения чисел с фиксированной запятой с помощью соответствующих алгоритмов сводится к операциям сложения и сдвига.
При умножении двух чисел произведение формируется суммированием частичных произведений. В зависимости от цифры множителя к сумме частичных произведений прибавляется либо множимое, либо ноль.
Произведение двух n – разрядных чисел с фиксированной запятой может иметь 2*n значащих разрядов. Поэтому необходимо предусмотреть возможность формирования в АЛУ произведения, имеющего двойную длину.
Структура АЛУ для выполнения умножения должна содержать регистры множимого, множителя и сумматор частичных произведений.
В зависимости от способа формирования суммы частичных произведений различают четыре метода выполнения умножения (рисунок 1):
1) начиная с младших разрядов множителя со сдвигом суммы частичных произведений вправо и при неподвижном множимом, регистры и сумматор частичных произведений имеют одинарную длину младших разрядов множителя со сдвигом суммы частичных произведений вправо и при неподвижном множимом;
;
2) начиная с младших разрядов множителя со сдвигом множимого влево и неподвижной сумме частичных произведений, регистр множимого и сумматор частичных произведений имеют двойную длину;
3) начиная со старших разрядов множителя со сдвигом суммы частичных произведений влево и неподвижным множимым, сумматор частичных произведений имеет двойную длину, регистр множителя и множимого одинарной длины;
4) начиная со старших разрядов множителя, со сдвигом вправо множимого и неподвижной сумме частичных произведений, сумматор частичных произведений и регистр множимого имеют двойную длину.
Если необходимо получить произведение двойной длины, то наиболее экономичным является первый метод; если достаточно иметь произведение одинарной длины, то целесообразно использовать либо первый, либо четвертый метод умножения.
Рассмотрим метод умножения целых чисел с фиксированной запятой, представленных в прямом коде, начиная с младших разрядов, со сдвигом суммы частичных произведений вправо. Этот метод получил наибольшее применение в ЭВМ, так как позволяет использовать регистры одинарной длины.
Произведение в формате двойной длины имеет один знаковый разряд и 2*n-1 цифровых разрядов. Результат умножения n – разрядных чисел, где n-1 цифровых разрядов, содержит 2*(n-1)=2*n-2 цифровых разрядов.
При данном методе регистр множителя в АЛУ и сумматор частичных произведений должны иметь цепи сдвига вправо. Регистр множимого может не иметь цепей сдвига.
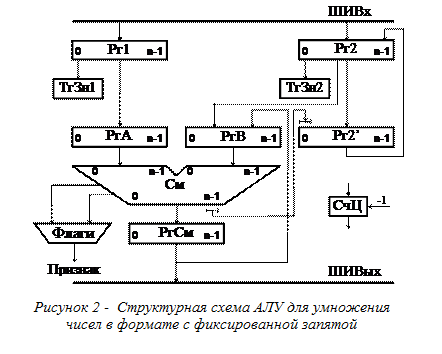
Структурная схема АЛУ для умножения n – разрядных целых двоичных чисел со знаком представлена на рисунке 2.
Схему АЛУ, выполняющего умножение двух чисел с фиксированной запятой, составляют:
§ входной регистр множимого Pr1;
§ регистры множителя Pr2 и Pr2’, на которых с помощью косой передачи вправо выполняется сдвиг множителя вправо;
§ триггеры знаков ТгЗн1 и ТгЗн2 для хранения знаков множимого множителя соответственно;
§ сумматор См для образования суммы частичных произведений;
§ регистр PrA для формирования частичного произведения;
§ регистр PrB для накопления суммы частичных произведений;
§ регистр сумматора PrСм, где образуется новое значение суммы;
§ счетчик циклов СчЦ.
Умножение чисел с фиксированной запятой можно разделить на следующие этапы:
§ начальная установка;
§ вычисление сумм частичных произведений;
§ коррекция результата в формате двойной длины.

Рисунок 1 – Возможные методы выполнения операции умножения
АЛУ работает следующим образом:
1. Первоначально в первом такте на Pr1 поступает множимое, одновременно с приемом множимого обнуляется PrB, хранящий сумму частичных произведений, а в СчЦ заносится число обрабатываемых цифровых разрядов множителя;
2. Во втором такте на Pr2 поступает множитель;
3. В зависимости от значения (0 или 1) младшего разряда модуля множителя к частичному произведению прибавляется либо 0, либо модуль множимого, для чего соответствующее значение присваивается PrA; на сумматоре См производится суммирование PrA и PrB; полученная сумма сдвигается путем передачи кода с выхода сумматора на регистр сумматора PrСм со сдвигом на один разряд вправо, и затем передается в регистр PrB.
4. Содержимое регистра Pr2 переносится в Pr2’ со сдвигом вправо на один разряд. Разряд «0» в Pr2’ оказывается свободным и в него заносится младший, (n - 1) – й, разряд суммы, выходящий при сдвиге за пределы разрядной сетки.
5. Содержимое Pr2’ переносится в Pr2 и тем самым завершается сдвиг множителя; содержимое СчЦ уменьшается на единицу и проверяется на равенство нулю.
6. Если СчЦ установится в нуль, нужно переходить к выдаче результата; в противном случае – переходить к анализу младшего разряда Pr2.
Когда СчЦ установится в 0, в PrСм и Pr2 будут содержаться соответственно старшие и младшие разряды модуля произведения, требующие сдвига на один разряд вправо для правильного расположения в формате двойного слова.
После выполнения этого сдвига результат операции из PrСм и Pr2 последовательно поступает на шину выхода.





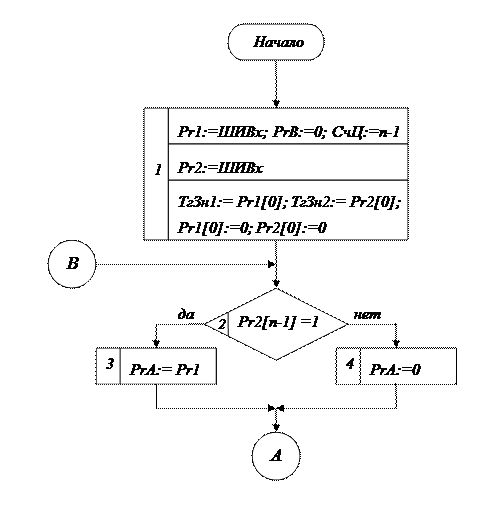
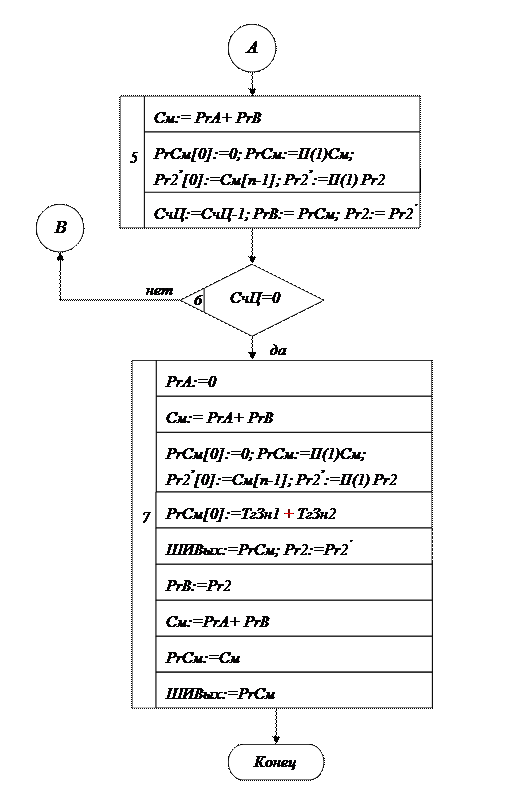
Рисунок 3 – Алгоритм умножения чисел с фиксированной запятой
Пусть X =+125, Y = -12. Вычислить Z=X*Y=125*(-12)= -1500, где X, Y, Z – числа с фиксированной запятой.
Используем алгоритм умножения целых чисел со знаком в формате с фиксированной запятой, начиная с младших разрядов, со сдвигом суммы частичных произведений вправо.
В данном примере для представления чисел X и Y выделим 8 разрядов, причем старший разряд знаковый (7 циклов умножения).
Умножение чисел с фиксированной запятой представим в виде таблицы (Таблица 1 – Умножение чисел с фиксированной запятой).
Таблица 1 - Умножение чисел с фиксированной запятой
| № бл. | СчЦ | Рг1 | Рг2 | РгA | РгB | См | РгСм | Рг2’ |
| № бл. | СчЦ | Рг1 | Рг2 | РгA | РгB | См | РгСм | Рг2’ |
Результат умножения чисел в формате двойной длины представлен на рисунке 4.
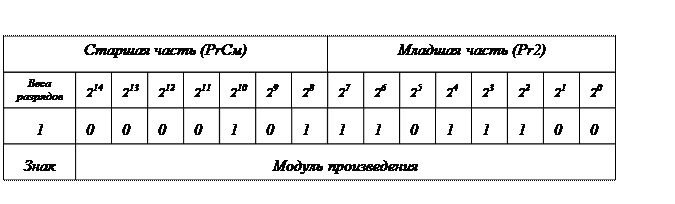
Рисунок 4 - Число Z = X × Y =125×(-12)= -1500 с фиксированной
запятой в формате двойной длины
 |