Национальный исследовательский университет
А.В. Якимов
ФИЗИКА ШУМОВ И ФЛУКТУАЦИЙ ПАРАМЕТРОВ
Электронное учебное пособие
Рекомендовано Учёным советом радиофизического факультета для студентов ННГУ, обучающихся по направлению подготовки
011800 “Радиофизика”.
Нижний Новгород 2013
УДК 621.391.822
ББК 32.841
Я45
Я45 Якимов А.В. ФИЗИКА ШУМОВ И ФЛУКТУАЦИЙ ПАРАМЕТРОВ:
Электронное учебное пособие. – Нижний Новгород: Нижегородский госуни- верситет, 2013. – 85 с.
Рецензенты:
заведующий отделом терагерцовой спектроскопии Института физики микро- структур РАН к.ф.-м.н. В.Л. Вакс,
заведующий кафедрой «Информационные технологии в физических исследова- ниях» физического факультета ННГУ д.т.н., профессор В.Р. Фидельман.
Настоящее пособие представляет собой раздел курса по выбору “Физика шумов и флуктуаций”.
Целью курса является ознакомление с физическими механизмами воз- никновения, методами учёта и описания электрических шумов и флуктуаций параметров в радиоэлектронных приборах (в основном, твердотельных).
Пособие предназначено для магистрантов радиофизического факультета ННГУ, обучающихся по направлению подготовки 011880 “Радиофизика”.
В основу пособия легли курсы лекций, читавшиеся автором студентам старших курсов радиофизического факультета на протяжении более 15 лет.
Ответственные за выпуск:
председатель методической комиссии радиофизического факультета ННГУ, к.ф.-м.н., доцент Н.Д. Миловский,
д.ф.-м.н., профессор Е.З. Грибова.
УДК 621.391.822
ББК 32.841
© А.В. Якимов, 2013
© Нижегородский государственный университет им. Н.И. Лобачевского, 2013
ОГЛАВЛЕНИЕ
Введение.................................................................................................................................. 5
1. Классификация и описание шумов............................................................................... 7
2. Тепловой шум.................................................................................................................. 12
3. Дробовой шум................................................................................................................. 20
4. Генерационно–рекомбинационный шум................................................................... 25
Общие сведения.......................................................................................................... 25
Уравнение Ланжевена для ГРШ............................................................................. 26
Вывод уравнения Ланжевена................................................................................... 27
Спектр генерационно–рекомбинационного шума............................................. 30
Мультипликативный характер ГРШ....................................................................... 32
5. Шум лавинообразования.............................................................................................. 35
Введение....................................................................................................................... 35
Спектр стационарного шума. Формула А.С. Тагера.......................................... 37
Статистический анализ процесса лавинообразования...................................... 39
Элементы теории “горячих” носителей тока.................................................... 39
Шум развитого лавинного пробоя...................................................................... 40
5.4.2. Шум частичного лавинного пробоя.............................................................. 42
6. Взрывной шум.................................................................................................................. 44
7. Фликкерный шум............................................................................................................. 47
Введение....................................................................................................................... 47
Форма спектра фликкерного шума........................................................................ 48
Спектрально-корреляционный анализ фликкерного шума 50
Нестационарность фликкерного шума.................................................................. 52
Мультипликативность фликкерного шума........................................................... 53
Эксперимент 1................................................................................................................ 53
Эксперимент 2................................................................................................................ 54
8. Основные модели фликкерного шума....................................................................... 57
Модель Дю Пре – Ван дер Зила.............................................................................. 57
Спектр фликкерного шума как суперпозиция лоренцевых
спектров........................................................................................................................... 57
Термоактивированные процессы, как причина фликкерного шума.................... 61
Модель Мак Уортера – Ван дер Зила.................................................................... 62
Фликкерные импульсные последовательности................................................... 63
Общий подход.......................................................................................................... 63
Модель Шенфельда – Малахова......................................................................... 64
Модель Халфорда................................................................................................... 66
Фликкерный шум как суперпозиция случайных процессов телеграфного типа 67
Модель двухуровневых систем.................................................................................... 69
Эмпирическая формула Хоухе – Клайнпеннина – Фандамме 70
9. Методы эквивалентного представления шумов....................................................... 72
Коэффициент шума двухполюсника...................................................................... 73
Эквивалентная шумовая температура................................................................... 74
Эквивалентное шумовое сопротивление.............................................................. 75
Эквивалентная шумовая проводимость................................................................ 75
Взаимосвязь шумовых параметров формулы Найквиста................................. 76
Эквивалентный шумовой ток (насыщенного диода).......................................... 78
Взаимосвязь описаний по Найквисту и Шотки.................................................... 78
Контрольные вопросы........................................................................................................ 80
Библиография....................................................................................................................... 83
ВВЕДЕНИЕ
Цель курса – ознакомление с физическими механизмами шумообразова- ния, методами учета и описания шумов и флуктуаций параметров в радиоэлек- тронных приборах (в основном, твердотельных).
Термины “шум” и “флуктуации” можно рассматривать как синонимы. Однако, как правило, под шумами подразумеваются электрические шумы, на- пример, шумы напряжения и тока. Термин “флуктуации” ассоциируется с флук- туациями параметров, например, сопротивления, либо ёмкости радиоэлектрон- ного элемента.
Шумы являются фактором, ограничивающим функциональные возмож- ности практически всех радиоэлектронных устройств. В качестве примера можно привести следующие важные для нас приложения:
- радиосвязь;
- измерительные устройства (прецизионные);
- стандарты частоты и времени.
Рассмотрим, например, радиосвязь, условная структура которой приведе- на на Рис. 0.1.
Передающая станция
Шумы тракта распространения
Приемная станция
Сигнал “чистый”
Сигнал искаженный
Собственные шумы
Собственные шумы
Рис. 0.1. Условная структура системы радиосвязи с выделенными источ- никами шумов
Здесь выделены источники действующих шумов, которые присутствуют не только в передающей и приёмной станциях, но и в тракте распространения сигнала (например, радиоволны). Эти шумы (а также флуктуации параметров) ограничивают как дальность, так и надёжность передачи полезного сигнала.
Другим примером являются шумы и флуктуации параметров в стандар- тах частоты и времени.
На сегодняшний день долговременная относительная стабильность часто- ты стандарта, составляющая f = 10-14, является пройденным этапом. Не вдава- ясь в детали приведенного термина, отметим, что точность хода часов, осно- ванных на таком стандарте, составляет 1 мкс за 3 года (примерно 108 с).
Однако для ряда задач такая точность не является достаточной.
В частности, для проверки основных положений общей теории относи- тельности требуется стабильность частоты порядка 10-15 (см., например, [1], разд. 8), кстати, уже достигнутая.
1. КЛАССИФИКАЦИЯ И ОПИСАНИЕ ШУМОВ
Этот раздел носит условный характер. Поскольку шумы существуют, их надо классифицировать.
Существуют разные, сложившиеся исторически, методы классификации шумов:
- естественные и технические;
- аддитивные и мультипликативные.
Естественными называют шумы, вызванные фундаментальными физи- ческими причинами, например,
- диссипацией энергии,
- дискретностью заряда электрона, q e= 1.6·10-19 Кл.
К техническим относят шумы, вызванные несовершенством технологии изготовления прибора. Исторически техническим называли фликкерный шум – весьма специфический тип шума, о котором, как и об остальных шумах, речь пойдет ниже. В настоящее время термин “технический шум” практически не используется.
Аддитивным называют шум, обычно в токе, либо напряжении, статисти- ческие характеристики которого не зависят от напряжения, приложенного к прибору, либо протекающего через прибор тока.
Например, аддитивным является тепловой шум, выделяющийся на рези- сторе, см. Рис. 1.1. Полное напряжение V, выделяющееся на резисторе, содер- жит две компоненты:
V (t) = V 0 + e T(t).
Здесь V 0 = I 0· R – падение напряжения на резисторе, e T(t) – эдс теплового шума, генерируемого резистором.
Тепловой шум моделируется на представленном рисунке эквивалентным генератором напряжения. Этот шум всегда присутствует на выводах резисто- ра. Его статистические характеристики не зависят от величины тока I 0, проте- кающего через резистор.
Под мультипликативным понимается шум, вызванный флуктуациями параметров элемента и проявляющийся при приложении напряжения к этому элементу, либо пропускании через него электрического тока.
Например, мультипликативную природу имеет шум v (t), выделяющийся на резисторе, обладающем флуктуациями сопротивления, см. Рис. 1.2.
Допустим, что сопротивление R резистора подвержено флуктуациям:
R º R (t) = R 0 + D R = R 0×(1 + d R).
Здесь R 0 – невозмущенное сопротивление резистора, D R = D R (t) – абсолютные флуктуации, d R = D R (t)/ R 0 – относительные флуктуации сопротивления.
При пропускании через резистор фиксированного тока I 0 на его выводах выделяется напряжение
V (t) = V 0 + v (t).
Здесь V 0 = I 0· R 0 – невозмущенное значение падения напряжения на резисторе. Шумовое напряжение v (t) обусловлено наличием флуктуаций сопротивления:
v (t) = I 0×D R (t) = V 0×d R (t).
Видим, что шумовое напряжение является лишь отображением флуктуа- ций сопротивления резистора. В данном примере эти флуктуации являются первичным источником. Они имеют мультипликативный характер. То есть для наблюдения флуктуаций сопротивления необходимо пропустить через резистор электрический ток, либо приложить напряжение.
При этом подразумевается, что статистические характеристики флуктуа- ций сопротивления не зависят ни от приложенного напряжения, ни от проте- кающего тока.
I 0
I 0
R
R (t)
V 0+ v (t)
e T(t)
Рис. 1.1. Резистор с учетом эдс тепло- вого шума
Рис. 1.2. Резистор, обладающий флук- туациями сопротивления
Перейдём к описанию статистических характеристик случайных процес- сов (см. например, [2], [3], [4], [5]).
Функция корреляции x (), если она существует, определяется для слу- чайного процесса x (t) следующим образом:
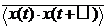Φx () =.
(1.1)
Здесь угловые скобки <…> означают усреднение по полному ансамблю реали- заций, а черта сверху – усреднение по времени. Из приведенного определения, в частности, следует, что полная мощность случайного процесса x (t) определя- ется значением функции корреляции при нулевом аргументе:
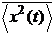= Φx (0).
(1.2)
Перейдем к спектрам.
В теоретическом анализе удобно использовать понятие математическо- го (двухстороннего) спектра Sx (), определенного для отрицательных и поло- жительных угловых частот Î(–¥; +¥). Этот спектр и функция корреляции
x () являются парой Фурье–сопряженных функций:
¥
Sx () =
ò Φx () exp(- j) d,
-¥
(1.3)
¥ d
Φx () =
ò Sx () exp(j).
|
Обе эти функции обладают свойством чётности:
Sx (- ) = Sx (),
Φx (- ) = Φx ().
(1.4)
Подставим во второе соотношение системы (1.3) =0 и учтём, что exp(0) =1. Учтём затем определение полной мощности случайного процесса че- рез функцию корреляции, представленное соотношением (1.2). В результате получим соотношение, разъясняющее смысл спектра процесса:
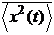¥ d
(1.5)
– спектр есть разложение полной мощности процесса по частоте. Здесь учтено свойство чётности спектра, позволившее перейти к интегрированию только по положительным частотам.
В измерениях используется так называемый физический спектр < x 2> f. Он является односторонним и определён для циклической частоты f = /2 , f ³0. Учитывая смысл спектра, представленный соотношением (1.5), для физи- ческого спектра имеем:
¥
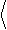
x 2 (t)
= ò< x 2 > f
df.
(1.6)
Сравнивая два представленных разложения полной мощности процесса по частоте, найдем связь между физическим (односторонним) и математиче- ским (двухсторонним) спектрами:
|
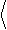
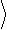
f
³ 0.
(1.7)
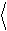
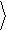
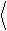
В соответствии со смыслом спектра, как разложения полной мощности, определим мощность процесса, сосредоточенную в диапазоне частот [ f 1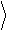, f 2]:
f 2
Примечание.
x 2 (D f) = ò x 2
f 1
df, D f
f
= f 2 -
f 1.
(1.8)
Здесь в обозначении мощности < x 2(D f)>, с целью упрощения записи, опущена черта сверху, означающая усреднение по времени. Однако это усред- нение необходимо в случае, если анализируемый процесс x (t) является неста- ционарным.
Определим понятие эффективного значения шума xeff. Под этой вели- чиной принято понимать квадратный корень из мощности шума:
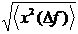xeff =.
(1.9)
Если шум является белым, либо полоса анализируемых частот достаточно мала, так что < x 2> f =const при f Î[ f 1, f 2], то
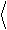
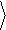
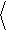x 2 (D f) = x 2
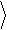× D f.
f
(1.10)
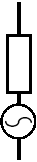
Соотношения (1.9) и (1.10) иногда используются для описания источни- ков шумов в радиоэлектронных схемах. Пример такого описания приведён на Рис. 1.3.
R
 |
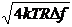Рис. 1.3. Резистор с источником теплового шума
На рисунке изображён резистор и источник напряжения генерируемого им теплового шума. Надпись рядом с генератором напряжения, моделирующим тепловой шум, характеризует эффективное напряжение шума в полосе D f.
Из соотношения (1.10) можно определить размерность спектра:
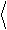
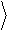é 2 ù
[ x ]2 [ x ]2
 | |
ëê x f úû=
[ f ] =Гц.
(1.11)
Например, для спектра шумового напряжения получим
|
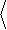
ë
ù= В2 / Гц.
|
Если же в роли анализируемого случайного процесса x (t) рассматривают- ся флуктуации частоты автоколебаний (например, стандарта частоты и време- ни), то для спектра получаем размерность Гц2/Гц (здесь “сокращать” герцы не рекомендуется, иначе может сложиться впечатление, что речь идёт о частоте, а не спектре).
Пример 1.1
Имеется белый шум e (t) со спектром < e 2> f = 2×10-20 В2/Гц.
Надо найти эффективное напряжение шума eeff в полосе частот усилителя низкой частоты (УНЧ), 0…20 кГц.
Решение
Используя соотношение (1.10), найдём выражение для мощности шума в заданной полосе частот:
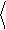e 2 (D f)
fв
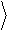
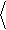= ò e 2
× df = e 2
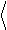f
f × fв.
Здесь верхняя частота fв = 20 кГц = 2×104 Гц.
Для полной мощности шума имеем
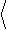
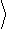e 2 (D f) = 2 ×10-20[В2 / Гц] × 2 ×104[Гц] = 4 ×10-16[В2 ].
Отсюда, согласно (1.9), находим эффективное напряжение шума:
eeff =2×10-8 В = 20 нВ.
В этом примере рассмотрен тепловой шум резистора с сопротивлением
R = 1 Ом при температуре T = 300о К. Если R = 106 Ом = 1 МОм, то eeff = 20 мкВ.
2. ТЕПЛОВОЙ ШУМ
Условие существования теплового шума – наличие диссипации энергии.
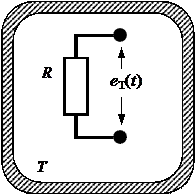
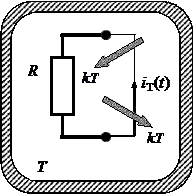
Рассмотрим идеальный резистор (Рис. 2.1), имеющий сопротивление R и находящийся в термостате при абсолютной температуре T.
 | |||
 | |||
а) б)
Рис. 2.1. Идеальный резистор в термостате:
(а) разомкнутые выводы; (б) короткозамкнутые выводы
На выводах разомкнутого резистора (Рис. 2.1-а) проявляется эдс теплово- го шума e T(t), возникающая из-за хаотического (теплового) движения носителей тока внутри его.
|
f = 4 kTR [В2/Гц]. (2.1)
Здесь k = 1,38×10-23 Дж/°К – постоянная Больцмана.
При замыкании выводов резистора (Рис. 2.1-б) через перемычку потечёт шумовой ток i T(t). Хотя этот ток обусловлен тепловым движением носителей в резисторе, можно также считать, что он обусловлен обменом квантами энергии между короткозамкнутым резистором и термостатом. Именно такой подход ис- пользуется в ФДТ (флуктуационно–диссипационной теореме).
Формула Найквиста для спектра тока теплового шума выглядит следую- щим образом:
< i T2> f = 4 kTG [А2/Гц]. (2.2)
Здесь G = 1/ R – проводимость резистора, выражаемая в Сименсах [Сим].
Приведем две эквивалентные схемы идеального резистора (Рис. 2.2), в которых тепловой шум учитывается либо эквивалентным генератором напря- жения e T(t), либо эквивалентным генератором тока i T(t).
R
R
e T(t)
а) б)
Рис. 2.2. Эквивалентные схемы для учета теплового шума: (а) генератором напряжения, (б) генератором тока.
Примечание.
Представленные схемы полностью эквивалентны друг другу.
Если резистор разомкнут, на его выводах действует эдс теплового шума e T(t). Генератор тока i T(t), в случае разомкнутого резистора, приводит к тому, что на резисторе выделяется напряжение
e T(t) = i T(t)· R.
При коротком замыкании резистор “отдает” во внешнюю цепь ток
i T(t) = e T(t)/ R.
Вышеприведенные варианты формулы Найквиста получены в рамках “классической” ФДТ, не учитывающей квантовомеханические эффекты. Имен- но поэтому полученный спектр не зависит от частоты, то есть тепловой шум имеет характер белого шума.
Этот результат, разумеется, не верен.
При f ® ¥ спектр должен достаточно быстро стремиться к нулю, так, чтобы на высоких частотах не было неинтегрируемой особенности. Иначе го- воря, тепловой шум должен иметь конечную мощность, удовлетворяя требова- нию недопустимости так называемой “ультрафиолетовой катастрофы”.
Учет квантовомеханических эффектов приводит к следующей модифика- ции формулы Найквиста для спектра эдс теплового шума:
|
|
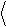
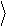
f
(hf / kT) exp(hf / kT)-1
[В2 / Гц].
(2.3)
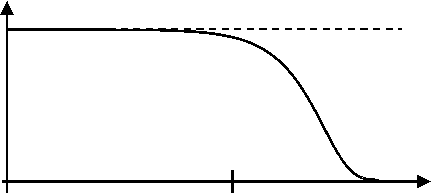
Здесь h = 6.626×10-34 Дж·с – постоянная Планка. Вид спектра теплового шума, полученный в рамках квантовой ФДТ, приведен на Рис. 2.3.
|
|
|
Рис. 2.3. Спектр эдс теплового шума согласно квантовой ФДТ
Верхняя частота, называемая также частотой среза, этого спектра равна
fв=kT / h. (2.4)
При T =300 0К данная частота равна 6.2×1012 Гц = 6.2 ТГц. Это соответст- вует длине волны, составляющей 0.05 мм. Таким образом, вплоть до миллимет- рового диапазона тепловой шум можно считать “белым”, то есть не учитывать зависимость его спектра от частоты. Однако для криогенной радиотехники в диапазоне СВЧ зависимость спектра теплового шума от частоты может ока- заться существенной.
Приведенная выше формула Найквиста справедлива только для идеаль- ного резистора. Реальные резисторы обладают инерционностью. Поэтому фор- мулу Найквиста следует модифицировать для комплексного линейного двухпо- люсника.
Импеданс Z () такого двухполюсника зависит от (угловой) частоты и состоит из вещественной и мнимой компонент:
Z () = R () + jB ().
Здесь R () = Re Z () – активное сопротивление двухполюсника, характери- зующее диссипацию энергии.
Таким образом, формула Найквиста для спектра эдс теплового шума при- нимает следующий вид:
< e 2 >
= 4 kT ·Re Z (2 f) [В2/Гц]. (2.5)
T f
Для спектра тока теплового шума короткозамкнутого двухполюсника, соответственно, имеем:
< i 2 >
= 4 kT ·Re Y (2 f) [А2/Гц]. (2.6)
T f
Здесь Y () = 1/ Z () – комплексная проводимость двухполюсника. Для активной компоненты проводимости имеем: Re Y () = G () = 1/ R ().
Пример 2.1
Интегрирующая RC – цепочка.
Найдем спектр и полную мощность на- пряжения теплового шума на выводах интег- R рирующей RC – цепочки (см. Рис. 2.4).
Комплексная проводимость цепочки есть сумма проводимостей резистора и кон- денсатора:
Z -1() = R -1 + jC.
Рис. 2.4
Отсюда находим вещественную часть импеданса. Затем, в соответствии с (2.5), определяем спектр теплового шума
|
|
|
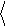
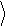
[В2 / Гц].
(2.7)
Здесь fc = 1/(2 c) – частота среза, определяемая постоянной времени цепочки
c = RC. Спектр, имеющий подобную зависимость от частоты, называется ло- ренцевым; его вид изображен на Рис. 2.5.
На нулевой частоте, f = 0, высота спектра максимальна и составляет 4 kTR, как у идеального резистора. Действительно, тепловой шум генерируется рези- стивным элементом R, а шунтирующее влияние конденсатора на этой частоте не проявляется.
При повышении частоты анализа f начинает проявляться шунтирующее влияние конденсатора C. В результате, при f ® ¥ спектр убывает по закону f -2.
< e 2 >
T f
4kTR
Рис. 2.5. Спектр теплового шума интегрирующей RC – цепочки
Вычислим полную мощность шума на выходе RC – цепочки:
|
|
¥
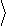
df
= kT.
C
(2.8)
|
|
в первой степени.
f =0
= 4 kTR, пропорциональна R 1, сопротивлению
- Ширина спектра, fc = 1/(2 RC), обратно пропорциональна сопротив- лению R.
В результате, полная мощность шума, определяемая площадью под гра- фиком спектра, не зависит от сопротивления R.
Данное объяснение, однако, не проясняет физической сути полученного результата, имеющего фундаментальный характер.
Действительно, устремим сопротивление к нулю, R ® 0. Обнаружим, что диссипация, как необходимое условие существования теплового шума, исчезла, а полная мощность шума осталась прежней.
Вопрос для самостоятельной проработки.
В чем допущена ошибка, либо в чем заключается фундаментальность по- лученного результата?
Ответы.
Вариант 1.
При R ® 0 высота спектра < e 2>
тоже стремится к нулю, а ширина – к
T f =0
бесконечности. Но, согласно формуле Найквиста (2.3), учитывающей кванто- вомеханические эффекты, ширина спектра ограничена сверху частотой среза fв, определённой соотношением (2.4). Поэтому представленный результат, полу- ченный в рамках классической ФДТ, неверен. При R = 0 полная мощность теп- лового шума равна нулю.
Вариант 2.
Преобразуем результат (2.8) для полной мощности теплового шума:
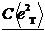kT
=. (2.8а)
2 2
Здесь в левой части представлена средняя энергия, накопленная конденсатором. Правая часть – энергия, приходящаяся на одну степень свободы. Таким обра- зом, мы просто вычислили энергию, которой конденсатор обменивается с тер- мостатом.
Пример 2.2
Последовательная RC – цепочка. Схема цепочки изображена на Рис. 2.6. Комплексный импеданс цепочки есть:
R C
Рис. 2.6
Z () = R - j.
C
Отсюда, согласно (2.5), находим спектр эдс теплового шума, проявляю- щегося на разомкнутых выводах цепочки:
< e 2 >
= 4 kTR [В2/Гц]. (2.9)
T f
Видим, что последовательно включенный конденсатор не влияет на спектр шума. Так как цепочка разомкнута, ток, протекающий через конденса- тор, равен нулю. Поэтому падение напряжения на конденсаторе тоже равно ну- лю.
Пример 2.3
Шум высокодобротного колебательного контура.
Рассмотрим колебательный контур, содержащий емкость C, индуктив- ность L и сопротивление потерь R (см. Рис. 2.7). На выводах разомкнутого кон- тура генерируется эдс теплового шума e T(t).
Контур характеризуется резонансной частотой
добротностью
f 1 =
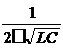
Q =2
,
L
f 1 L
R R
и полуполосой пропускания
B = f 1.
2 Q
Рис. 2.7
При описании колебательного контура используются дополнительные параметры: волновое сопротивление = 2 f 1 L и резонансное сопротивление Roe = Q 2 R.
Для определения спектра < e 2> теплового шума надо проанализировать
T f
выражение для комплексного импеданса контура:
Z () =
jC +1/(R +
jL)
, = 2 f.
(2.10)
Этот импеданс, отражая селективные свойства контура, имеет макси- мальное (вещественное) значение на резонансной частоте, Z (2 f 1)= Roe. При от- стройке от резонанса наблюдается быстрое убывание модуля импеданса.
Полагая для простоты, что контур имеет высокую добротность, Q >>1, получим следующее выражение для спектра теплового шума:
|
|
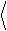
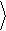
T f 1 + (F / B)2
, F = f
- f 1.
(2.11)
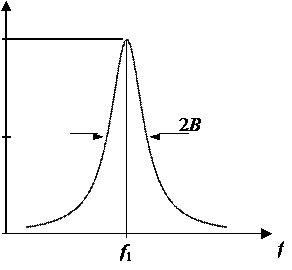
Здесь F – частота отстройки от резонанса. Вид спектра приведен на Рис. 2.8.
На резонансной частоте f 1 контур “шумит” как идеальный резистор, обла- дающий сопротивлением Roe. Форма спектра повторяет резонансную кривую контура, характеризующуюся шириной (на уровне 0.5), равной 2 B – удвоенной полуполосе пропускания.
< e 2 >
T f
4kTRoe
Рис. 2.8. Спектр теплового шума высокодобротного колебательного контура
Определим полную мощность теплового шума как площадь под графиком его спектра. Проводя необходимое интегрирование и осуществляя ряд преобра- зований, получим удивительный результат:
|
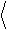
T C
Эта мощность не зависит от величины сопротивления потерь R даже при R ®0 (идеальный осциллятор) и имеет то же значение, что и для интегрирую- щей RC – цепочки, рассмотренной в Примере 2.1.
Качественно этот результат можно объяснить так же, как и в случае ин- тегрирующей RC – цепочки.
- Высота спектра, < e 2> = 4 kTR, пропорциональна R 1, сопротивле-
T f = f 1 oe
нию потерь в первой степени.
- Ширина спектра 2 B обратно пропорциональна сопротивлению R.
В результате, мощность шума, определяемая полной площадью под гра- фиком спектра, не зависит от сопротивления R.
Данное объяснение, однако, не проясняет физической сути полученного результата, имеющего фундаментальный характер.
Действительно, устремим сопротивление к нулю, R ® 0. Обнаружим, что диссипация, как необходимое условие существования теплового шума, исчезла, а полная мощность шума осталась прежней.
Вопрос для самостоятельной проработки.
В чем заключается фундаментальность полученного результата? Ответ.
Ситуация идентична рассмотренной в Примере 2.1, но с некоторой спе- цификой. При R ® 0 колебательный контур превращается в идеальный осцил- лятор, а спектр (2.11) трансформируется в дельта–функцию на частоте f 1