Определение оптимального объема материального потока.

Задача 2.

Основная цель деятельности любого звена логистический систе­мы – максимизация прибыли. Поэтому предприятию более вы­годно, если на единицу материального потока приходится мень­шая сумма постоянных затрат. Этого можно достичь, увеличивая объем производства и реализации продукции на уже имеющихся производственных мощностях. Но, принимая решение об увели­чении объемов производства, менеджер должен помнить, что нельзя произвольно увеличивать количество переменных факто­ров на единицу постоянного, поскольку в этом случае вступает в действие закон убывающей отдачи.

Согласно этому закону, начиная с определенного момента, последовательное присоединение единиц переменного фактора к неизменному фиксированному фактору приведет к прекраще­нию роста отдачи от него, а затем и к ее уменьшению.

Прирост затрат, связанный с производством дополнительной единицы материального потока, т. е. отношение прироста пере­менных затрат к вызванному ими приросту материалопотока, на­зывается предельными издержками (МС, англ. marginal cost).

(1)

где ∆VС — прирост переменных затрат;

∆Q — прирост материалопотока, вызванный изменением переменных затрат.

 

Получение максимальной прибыли возможно лишь при определенных условиях: сочетание объема материалопотока, из­держек на его производство и продвижение до конечного потре­бителя, а также продажной цены единицы материалопотока должно быть таким, чтобы предельные издержки на производ­ство и реализацию были равны предельному доходу (MR, англ. marginal return).

Предельный доход — это прирост выручки на единицу прирос­та объема материального потока:

 

(2)

где R — доход предприятия за период, д. е.;

R = p·Q (3)

где р — цена реализации единицы материалопотока.

При этом необходимо учитывать, что не всякое расширение производства влечет за собой адекватное увеличение прибыли, так как изменение издержек происходит по-разному и при росте объемов производства происходит снижение цен.

Существует несколько способов определения оптимального объема материального потока, при котором предприятие получит максимальную прибыль:

бухгалтерско - аналитический;

графический;

метод наименьших квадратов.

Сущность бухгалтерско-аналитического способа состоит в со­поставлении предельного дохода и предельных издержек. Ес­ли предельный доход больше предельных издержек, то дальней­ший рост выпуска увеличивает общую сумму прибыли, и наобо­рот. Следовательно, для максимизации прибыли предприятие должно увеличивать объем вырабатываемого материального потока до тех пор, пока предельный доход выше предельных издержек, и прекратить его увеличение, как только предельные издержки начнут превосходить предельный доход.

При графическом методе необходимо на один график нанес­ти кривые зависимости предельных издержек и предельных зат­рат от объема материального потока. Максимальная прибыль — это точка пересечения кривой предельных издержек с кривой предельного дохода. После этой точки кривая предельных издер­жек располагается выше кривой предельного дохода, из чего сле­дует, что каждая дополнительная единица материального потока уменьшает прибыль, и ее производство неэффективно для пред­приятия.

Сущность метода наименьших квадратов заключается в том, что на основании массовых данных и используя корреляционно-регрессионный анализ, исследуется зависимость предельного до­хода и предельных издержек от объема материального потока. Исходя из вида зависимости между предельным доходом и объемом материального потока, предельными издержками и объемом материального потока следует выбрать вид кривой, максимально близко приближающуюся (описывающую) эмпирическую зависимость. В качестве таких зависимостей или кривых, которыми можно описать эмпирические зависимости, могут служить:

(4)

Суть метода наименьших квадратов заключается в следующем. Пусть результаты измерений представлены таблицей:

Таблица 1 – Экспериментальные (эмпирические) значения исследуемых параметров

x	x1	…	xn
y	y1	…	yn

Будем считать, что вид аппроксимирующей (приближающей) зависимости выбран и ее можно записать следующим образом:

(5)

где f - известная функция,

a ₀, a ₁, …, a _m – неизвестные постоянные параметры, значения которых надо найти. В методе наименьших квадратов приближение функции (5) к экспериментальной зависимости считается наилучшим, если выполняется условие:

(6)

Функция R называется невязкой.

Т.к. невязка

,

то она имеет минимум. Необходимым условием минимума функции нескольких переменных является равенство нулю всех частных производных этой функции по параметрам. Таким образом, отыскание наилучших значений параметров аппроксимирующей функции (6), то есть таких их значений, при которых R = R (a ₀, a ₁, …, a _m) минимальна, сводится к решению системы уравнений:

(7)

Пример 2.1. На основании данных о работе склада (табл. 2.1) необходимо определить оптимальный грузооборот, при котором склад получит максимальный размер прибыли. Грузооборот склада – натуральный объемный показатель работы скла­да (базы, предприятия по поставкам), показывающий количество продук­ции, отправленной за определенный период времени.

Данные табл. 2.1 показывают, что самый выгодный объем гру­зооборота – 8 тыс. т. Затем предельные издержки уже превосхо­дят предельный доход, что явно неблагоприятно для предприя­тия. Следовательно, складу экономически выгодно принимать на хранение до 8 тыс. т материальных ресурсов.

Практически такой же результат дает и графический метод (рис. 2.1).

До 8 тыс. т кривая предельных издержек (MС) ниже кривой предельного дохода и поэтому каждая дополнительная единица грузооборота увеличивает сумму прибыли.

Данные таблицы и графика позволяют сделать вывод, что зависимость между предельным доходом и объемом грузооборота может быть описана уравнением прямой:

 

MR = a + b · Q, (8*)

 

где MR – предельный доход на единицу продукции;

Q – грузооборот склада в натуральном выражении.

 

С помощью метода наименьших квадратов определим неизвестные параметры a и b. Определение неизвестных коэффициентов реализуем путем решения системы уравнений по типу приведенной (7):

(8)

Определим частные производные по каждому из уравнений системы (8):

Упростим первое уравнение системы:

(9)

Упростим второе уравнение системы:

(10)

Таким образом, система (8) примет вид:

(11)

Решим систему уравнений (8) используя формулы Крамера. Для этого запишем систему (8) в матричной форме:

 

, (12)

 

где A – матрица коэффициентов при неизвестных a и b:

X – матрица-столбец неизвестных системы:

B – матрица правых частей системы:

Умножив обе части уравнения системы (12) слева на A ^-1, получим:

(13)

где A ^-1 – матрица обратная исходной матрице A (исходной матрицы на ее обратную матрицу образует единичную матрицы, т. е. матрицу того же размера, что и матрица A, но с элементами диагонали матрицы, равными единицам):

(14)

где detA – определитель исходной матрицы А:

(15)

 

A ^* – союзная матрица к матрице A:

(16)

Элементы матрицы A ^* называются алгебраическими дополнениями исходной матрицы A. Алгебраическим дополнением элемента матрицы называется минор этого элемента, взятый со знаком «плюс», если сумма порядковых номеров строки и столбца, на пересечении которых расположен этот элемент, равна четному числу, в противном случае минор берем со знаком «минус».

Минором некоторого элемента матрицы называется определить этой матрицы, полученный из исходного определителя матрицы путем вычеркивания строки и столбца на пересечении которых расположен выбранный элемент:

Таким образом, союзная матрица A ^* примет вид:

(17)

Перемножим союзную матрицу на матрицу правых частей:

 

Необходимо произведение союзной матрицы и матрицы правых частей умножить на 1/ detA:

 

(18)

Матрица (18) – это результат перемножения обратной матрицы A ^-1 на матрицу правых частей В. Перепишем уравнение (13) в виде:

(19)

В результате всех преобразований получим:

 

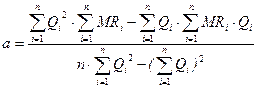(20)

 

(21)

Используя формулы (20) и (21) определим коэффициенты прямой зависимости предельного дохода от грузооборота:

 

.

 

 

 

Определив коэффициенты прямой a и b для случая зависимости предельного дохода от величины грузооборота уравнение прямой можно записать в виде:

MR = 320 –20 · Q

Таким же образом определим зависимость общих издержек от величины грузооборота:

 

 

 

Зависимость общих издержек от величины грузооборота примет вид:

TC = 325,7 + 139,5 · Q

 

Зависимость предельных издержек от объема производства продукции можно описать уравнением параболы:

 

MC = a + b · Q + c· Q ²

Для определения неизвестных коэффициентов параболы а, b, c воспользуемся методом наименьших квадратов. Составим систему уравнений (7):

(22)

Определим частные производные по каждому из уравнений системы (22):

 

 

 

Упростим первое уравнение системы:

Упростим второе уравнение системы:

Упростим третье уравнение системы:

Тогда система уравнений примет вид:

(23)

Решим систему уравнений используя формулы Крамера и приведенный выше алгоритм (см. формулы (12) – (19)).

Определитель исходной матрицы А:

 

 

Определим элементы союзной матрицы А*:

 

 

 

 

 

Все элементы союзной матрицы А* определены. Далее необходимо только лишь перемножить матрицы А* и B, а такжеподелить получившиеся элементы матрицы-столбца на определитель исходной матрицы A:

 

Проведя необходимые расчеты и определив неизвестные коэффициенты a, b, с запишем зависимость предельных издержек от величины грузооборота:

 

MC = 203,75 – 24,527 Q + 2,3674 Q ².

 

Приравняв предельный доход и предельные издержки, можно найти величину оптимального грузооборота, который обеспечит максимальную сумму прибыли:

320 - 20· Q = 203,75 – 24,527 Q + 2,3674 Q ²;

 

2,3674 Q ² - 4,527 Q – 116,25 = 0;

 

Приведенные расчеты показывают, что оптимальный объем грузооборота составляет 8028 т.

При таком объеме выручка составит:

 

R = p·Q = 230·8,028 = 1846,44 тыс. у.д.е.

 

Зависимость общей суммы издержек от объема грузооборота имеет следующий вид:

 

ТС = 325,7 + 139,5 · 8,028

 

Издержки хранения составят:

 

ТС = 67,727 + 154,32·8,028 = 1445,61 тыс. у. д. е.

 

Прибыль будет равна:

 

П = R – ТС = 1846,44 – 1445,61 = 400,83 тыс. у. д. е.

 

Следовательно, данному складу можно наращивать объемы грузооборота до 8028 т при условии, что себестоимость хранения одной тонны не повысится.

 

Таблица 2.1

Рис. 2.1. Предельные издержки и доход на единицу грузооборота

 

Задача 2.2. Фирма «Феникс», оказывающая складские услуги торговым фирмам города, решила открыть новый склад. Прог­нозируемые данные о работе нового склада представлены в таблице. Необходимо определить оптимальный объем грузо­оборота на складе, при котором фирма «Феникс» сможет полу­чить максимальный уровень прибыли:

бухгалтерско-аналитическим методом;

графическим методом;

методом наименьших квадратов.