Криволинейные интегралы
- Криволинейные интегралы первого рода
Криволинейный интеграл представляет собой обобщение определенного интеграла на случай, когда функция задана не на отрезке  , а на кривой
, а на кривой 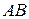 .
.
Пусть задана непрерывная плоская спрямляемая кривая 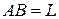 , в каждой точке
, в каждой точке  которой определена непрерывная функция
которой определена непрерывная функция 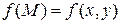 . Разобьём кривую
. Разобьём кривую  точками
точками  на
на  элементарных дуг, выберем на каждой такой дуге
элементарных дуг, выберем на каждой такой дуге  произвольно точку
произвольно точку  , вычислим значения
, вычислим значения  . Умножим это значение на длину частичной дуги
. Умножим это значение на длину частичной дуги 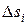 и составим интегральную сумму
и составим интегральную сумму

Если при стремлении 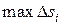 к нулю эта интегральная сумма имеет конечный предел, не зависящий ни от способа разбиения кривой
к нулю эта интегральная сумма имеет конечный предел, не зависящий ни от способа разбиения кривой  на части, ни от выбора точек
на части, ни от выбора точек  , то этот предел называется криволинейным интегралом первого рода от функции
, то этот предел называется криволинейным интегралом первого рода от функции 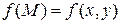 , взятым по кривой
, взятым по кривой  , и обозначается
, и обозначается
 (1)
(1)
Особенность этого интеграла состоит в том, что он не зависит от направления кривой  . К криволинейным интегралам первого рода естественно приводят задачи, связанные с массами, непрерывно распределенными вдоль некоторой кривой. Так, если в каждой точке материальной кривой
. К криволинейным интегралам первого рода естественно приводят задачи, связанные с массами, непрерывно распределенными вдоль некоторой кривой. Так, если в каждой точке материальной кривой  задана линейная плотность
задана линейная плотность 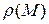 , то масса всей кривой равна
, то масса всей кривой равна
 . (2)
. (2)
Аналогично для пространственной кривой
 .
.
Длина дуги находится по формуле
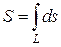 (3)
(3)
Криволинейный интеграл первого рода сводится к обыкновенному определенному интегралу.
Пусть плоская кривая  задана параметрическими уравнениями
задана параметрическими уравнениями
 ,
, 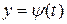
 ,
,
где функции 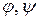 непрерывны и непрерывно дифференцируемы. Предположим также, что на кривой нет кратных точек. Тогда (см. приложения определенных интегралов) кривая
непрерывны и непрерывно дифференцируемы. Предположим также, что на кривой нет кратных точек. Тогда (см. приложения определенных интегралов) кривая  спрямляема и
спрямляема и
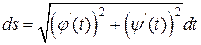 . (4)
. (4)
Здесь предполагается, что возрастание дуги  соответствует возрастанию параметра
соответствует возрастанию параметра  . Переходя в интеграле (1) к переменной
. Переходя в интеграле (1) к переменной  , получим
, получим
 (5)
(5)
Таким образом, для вычисления криволинейного интеграла первого рода надо в подынтегральной функции заменить  их параметрическими представлениями, а дифференциал дуги заменить по формуле (5).
их параметрическими представлениями, а дифференциал дуги заменить по формуле (5).
Если кривая  задана явным уравнением
задана явным уравнением 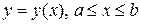 (в роли параметра – переменная
(в роли параметра – переменная  ), то формула (5) принимает вид
), то формула (5) принимает вид
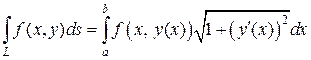 (6)
(6)
Основные свойства криволинейных интегралов первого рода аналогичны свойствам определенного интеграла.
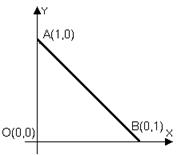 Пример 1. Вычислить интеграл
Пример 1. Вычислить интеграл 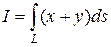 , где
, где  – контур треугольника с вершинами
– контур треугольника с вершинами  .
.
Решение. Линия  состоит из трех прямолинейных отрезков
состоит из трех прямолинейных отрезков  и
и  . Поэтому представим интеграл в виде суммы
. Поэтому представим интеграл в виде суммы 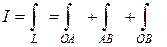 . Вычислим последовательно
. Вычислим последовательно
 ;
;
 ;
;
 .
.
Значит, 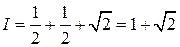 . ☻
. ☻
Пример 2. Вычислить интеграл  , где
, где  – лежащая в первом квадранте четверть эллипса
– лежащая в первом квадранте четверть эллипса 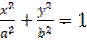 .
.
Решение. Используем параметрическое задание эллипса

Находим  и по формуле (4) подсчитаем
и по формуле (4) подсчитаем 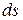 :
:
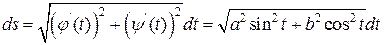 .
.
По формуле (5) запишем
 .
.
Множитель  наталкивает на мысль перейти к двойному углу:
наталкивает на мысль перейти к двойному углу:

 .
.
Подынтегральная функция подсказывает замену:
 .
.
Получаем 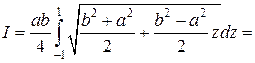
 . ☻
. ☻
Пример 3. Найти длину дуги пространственной кривой  от точки
от точки  до точки
до точки  .
.
Решение. Точке  соответствует значение параметра
соответствует значение параметра  , для точки
, для точки  параметр
параметр  . Найдем
. Найдем  . Для пространственной кривой вычислим
. Для пространственной кривой вычислим 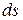 по формуле, аналогичной формуле (4):
по формуле, аналогичной формуле (4):

 .
.
Длину дуги найдем по формуле (3):
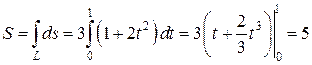 . ☻
. ☻
Пример 4. Найти массукривой  , если линейная плотность в каждой точке равна
, если линейная плотность в каждой точке равна  .
.
Решение. Чтобы воспользоваться формулой (2), вычислим
 . По условию
. По условию  .
.
Массу кривой найдем по формуле (2)


 . ☻
. ☻
Криволинейные интегралы второго рода
Рассмотрим непрерывную кривую  , в каждой точке которой задана непрерывная функция
, в каждой точке которой задана непрерывная функция 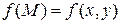 . Разобьем кривую точками
. Разобьем кривую точками  на
на  частей, выберем на каждой частичной дуге
частей, выберем на каждой частичной дуге  произвольную точку
произвольную точку 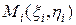 и вычислим в этой точке значение функции
и вычислим в этой точке значение функции 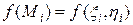 . Но это значение мы умножим на этот раз не на длину дуги, а на величину проекции этой дуги, например, на ось абсцисс, т.е. на
. Но это значение мы умножим на этот раз не на длину дуги, а на величину проекции этой дуги, например, на ось абсцисс, т.е. на 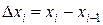 . Составим интегральную сумму
. Составим интегральную сумму

Если при стремлении к нулю  эта сумма имеет конечный предел, не зависящий ни от способа разбиения кривой, ни от выбора точек
эта сумма имеет конечный предел, не зависящий ни от способа разбиения кривой, ни от выбора точек  , то этот предел называется криволинейным интегралом второго рода от
, то этот предел называется криволинейным интегралом второго рода от 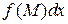 по кривой (по пути)
по кривой (по пути) 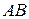 и обозначается символом
и обозначается символом
 . (1)
. (1)
Аналогично можно получить криволинейный интеграл второго рода от  :
:
 (2)
(2)
Если вдоль 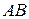 определены две функции
определены две функции  и
и  , то приходим к криволинейному интегралу
, то приходим к криволинейному интегралу
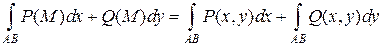 (3)
(3)
Так как проекция дуги на ось зависит от направления дуги и меняет знак с изменением этого направления, то для интеграла второго рода
 и
и  .
.
С точки зрения механики интеграл  представляет собой работу переменной силы
представляет собой работу переменной силы  , точка приложения которой описывает кривую
, точка приложения которой описывает кривую 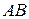 .
.
Аналогично вводится криволинейный интеграл второго рода по пространственной кривой:
 .
.
Пусть кривая 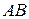 задана параметрическими соотношениями
задана параметрическими соотношениями
 ,
,
причем функции  непрерывны, а при изменении параметра
непрерывны, а при изменении параметра  от
от  до
до  кривая описывается именно в направлении от точки
кривая описывается именно в направлении от точки 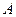 к точке
к точке  . Если речь идет об интеграле (1), то дополнительно требуется непрерывность производной
. Если речь идет об интеграле (1), то дополнительно требуется непрерывность производной 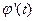 , для интеграла (2) – непрерывность производной
, для интеграла (2) – непрерывность производной 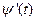 . При этих предположениях криволинейный интеграл второго рода существует и сводится к определенному интегралу
. При этих предположениях криволинейный интеграл второго рода существует и сводится к определенному интегралу
 (4)
(4)
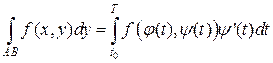 (5)
(5)
Порядок расстановки пределов соответствует выбранному на кривой направлению.
В частном случае, когда кривая 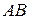 задана явным уравнением
задана явным уравнением 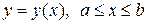 (в роли параметра – переменная
(в роли параметра – переменная  ), причем перемещение из
), причем перемещение из 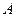 в
в  происходит при изменении
происходит при изменении  от
от 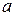 до
до  , формула (4) принимает вид
, формула (4) принимает вид
 (6)
(6)
Аналогично, если  , то формула (5) принимает вид
, то формула (5) принимает вид
 (7)
(7)
Пример 1. Вычислить интеграл 
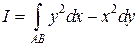 , где кривая
, где кривая 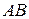 – верхняя половина окружности радиуса
– верхняя половина окружности радиуса  с центром в начале координат, начало пути – точка
с центром в начале координат, начало пути – точка 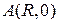 .
.
Решение. Параметрические уравнения заданной кривой
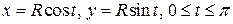 .
.
Точке  соответствует значение параметра
соответствует значение параметра 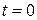 , для точки
, для точки  параметр
параметр  . Находим
. Находим 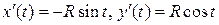 . По формулам (4) и (5) запишем
. По формулам (4) и (5) запишем
 .
.
Вычислим  ;
;
 . Значит,
. Значит,  . Заметим, что если бы путь интегрирования начинался в точке
. Заметим, что если бы путь интегрирования начинался в точке  , то получили бы результат с противоположным знаком:
, то получили бы результат с противоположным знаком:
 . ☻
. ☻
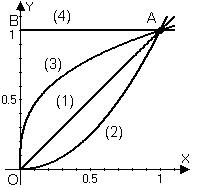 Пример 2. Вычислить интеграл
Пример 2. Вычислить интеграл  , где
, где 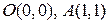 , а кривая
, а кривая 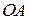 определяется уравнением 1)
определяется уравнением 1)  , 2)
, 2) 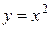 , 3)
, 3)  ; 4)
; 4) 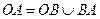 .
.
Решение. 1) Вдоль линии
 (в роли параметра –
(в роли параметра – 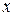 ).
).
Значит, 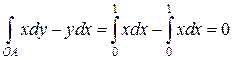 .
.
2) Вдоль линии  . Поэтому
. Поэтому  .
.
3) Вдоль линии  (в роли параметра –
(в роли параметра –  ). Получаем
). Получаем
 .
.
4) Путь интегрирования состоит из двух участков, значит, 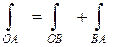 .
.
а) Вдоль отрезка  и
и  .
.
б) Вдоль отрезка 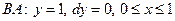 и
и 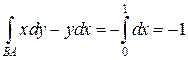 .
.
Получаем 
Результаты вычисления получились различными для разных путей интегрирования. ☻
Теорема. Пусть в односвязной области 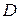 функции
функции 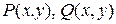 определены и непрерывны вместе со своими производными
определены и непрерывны вместе со своими производными  . Для того чтобы интеграл
. Для того чтобы интеграл  не зависел от пути интегрирования, необходимо и достаточно, чтобы подынтегральное выражение
не зависел от пути интегрирования, необходимо и достаточно, чтобы подынтегральное выражение 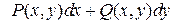 было полным дифференциалом.
было полным дифференциалом.
Теорема. Припредположениях предыдущей теоремыдля того, чтобы выражение  было полных дифференциалом, необходимо и достаточно выполнение условия
было полных дифференциалом, необходимо и достаточно выполнение условия
 . (8)
. (8)
Пример 3.. Вычислить интеграл  при условиях примера 2.
при условиях примера 2.
Решение.
1) Вдоль линии  ;
; 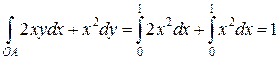 ;
;
2) Вдоль линии  ;
;  ;
;
3) Вдоль линии 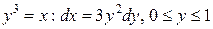 ;
; 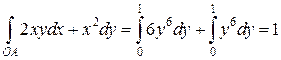 ;
;
4) Вдоль отрезка  и
и 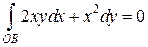 ,
,
вдоль 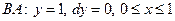 и
и  .
.
А в этом примере результат вычисления не зависит от выбора кривой, потому что здесь  – выполнено условие (8). Значит, подынтегральное выражение
– выполнено условие (8). Значит, подынтегральное выражение  есть полный дифференциал. Можно было сразу записать:
есть полный дифференциал. Можно было сразу записать:
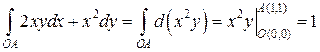 . ☻
. ☻
Пример 4. Найти работу, производимую силой тяжести при перемещении материальной точки массы  из точки
из точки  в точку
в точку  .
.
Решение. Сила тяжести есть вектор-функция 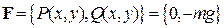 , здесь
, здесь  ,
, 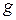 – ускорение свободного падения. Работа вычисляется с помощью криволинейного интеграла второго рода:
– ускорение свободного падения. Работа вычисляется с помощью криволинейного интеграла второго рода:
 .
.
 Заметим, что подынтегральное выражение есть полный дифференциал:
Заметим, что подынтегральное выражение есть полный дифференциал: 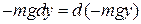 (выполнено условие
(выполнено условие  ), поэтому интеграл не зависит от пути интегрирования. Выберем путь из точки
), поэтому интеграл не зависит от пути интегрирования. Выберем путь из точки  в точку
в точку  по ломаной, звенья которой параллельны координатным осям (см. пример 2 путь (4)). Например, возьмем ломаную
по ломаной, звенья которой параллельны координатным осям (см. пример 2 путь (4)). Например, возьмем ломаную 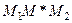 , где
, где  .
.
Теперь 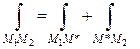 . Вдоль пути
. Вдоль пути 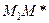 имеем
имеем  , поэтому
, поэтому 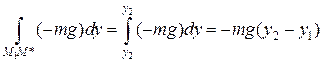 . Вдоль
. Вдоль  :
: 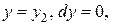 поэтому
поэтому  . Работа равна
. Работа равна  . ☻
. ☻
Пример 5. Вычислить интеграл  .
.
Решение. В условии не задан путь интегрирования, а заданы лишь начальная и конечная точки. Убедимся, что результат не зависит от пути. Здесь
 .
.
Условие (8) выполнено. Поэтому имеем право выбрать наиболее удобный путь интегрирования – например, ломаную  . Вдоль первого звена этой ломаной
. Вдоль первого звена этой ломаной 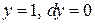 и
и 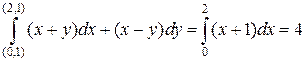 . Вдоль второго звена
. Вдоль второго звена  и
и 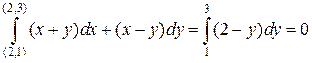 . Значит,
. Значит,  .
.
Можно было заметить сначала, что  и записать
и записать  ☻
☻
Покажем на примере, как восстановить функцию 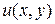 по ее полному дифференциалу
по ее полному дифференциалу  .
.
Пример 6. Восстановить функцию 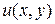 по ее полному дифференциалу
по ее полному дифференциалу  .
.
Решение. Убедимся сначала, что задан действительно полный дифференциал некоторой функции. У нас

Условие  выполнено. По определению, дифференциал функции двух переменных
выполнено. По определению, дифференциал функции двух переменных  , поэтому для восстановления функции
, поэтому для восстановления функции 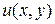 имеется два условия:
имеется два условия:
. 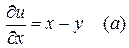 ,
, 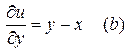
Начнем с условия 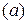 .
.
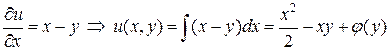 .
. 
Заметим, что при восстановлении первообразной функции одной переменной  по ее производной
по ее производной 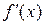 получаем результат с точностью до постоянного слагаемого
получаем результат с точностью до постоянного слагаемого  . Сейчас мы восстанавливаем функцию двух переменных по одной из ее частных производных (здесь – по
. Сейчас мы восстанавливаем функцию двух переменных по одной из ее частных производных (здесь – по  ), поэтому получаем результат с точностью до слагаемого
), поэтому получаем результат с точностью до слагаемого  , зависящего от другой переменной.
, зависящего от другой переменной.
Таким образом, появилась неизвестная функция  . Для ее определения послужит условие
. Для ее определения послужит условие  . С одной стороны, вычислим частную производную
. С одной стороны, вычислим частную производную  от функции
от функции  :
:  . С другой стороны, в силу условия
. С другой стороны, в силу условия  ,
,  . Из равенства
. Из равенства  получаем
получаем  . Значит, функция
. Значит, функция  принимает вид
принимает вид 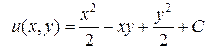 .
.
Можно начинать с условия  , тогда условие
, тогда условие 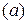 служит для определения функции
служит для определения функции  , появившейся в результате интегрирования по переменной
, появившейся в результате интегрирования по переменной 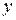 .
.
Возможен еще один способ решения. Из условий 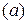 и
и  находим
находим
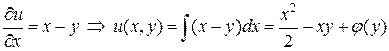
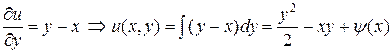 .
.
Сравним полученные выражения для  :
:

Значит, 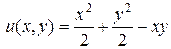 . ☻
. ☻
Формула Грина
Формула Грина связывает криволинейный интеграл по границе некоторой области с двойным интегралом по этой области:
 (1)
(1)
Формула Грина справедлива в следующих предположениях:
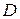 – конечная односвязная область,
– конечная односвязная область, 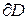 – ограничивающий эту область простой кусочно-гладкий контур, функции
– ограничивающий эту область простой кусочно-гладкий контур, функции  и их производные
и их производные  непрерывны в замкнутой области
непрерывны в замкнутой области  . При этом граница
. При этом граница 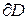 пробегается в положительном направлении (то есть так, что область
пробегается в положительном направлении (то есть так, что область 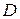 остается слева).
остается слева).
Из формулы (1) получаются формулы для вычисления площади области 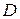
 (2а)
(2а)
 (2б)
(2б)
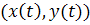 - параметрическое задание кривой
- параметрическое задание кривой  ,
, 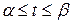 ).
).
 Пример 1. Вычислить интеграл
Пример 1. Вычислить интеграл  , где
, где  пробегаемый в положительном направлении контур, ограничивающий область
пробегаемый в положительном направлении контур, ограничивающий область
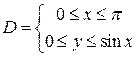 .
.
Решение. Чтобы воспользоваться формулой (1), запишем сначала
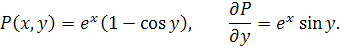

Так как  , то по формуле Грина запишем:
, то по формуле Грина запишем:

 . ☻
. ☻

Пример 2. Вычислить площадь
фигуры, ограниченной астроидой
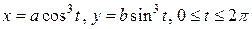 .
.
Решение. Чтобы воспользоваться формулой (2), подсчитаем
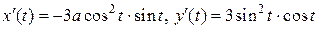 ,
,
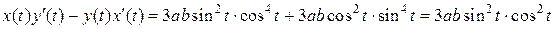 .Теперь
.Теперь
 . ☻
. ☻
Задания для самостоятельной работы.
1. Вычислить интеграл 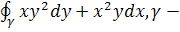 окружность
окружность 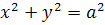 .
.
Ответ. 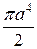
2.  - эллипс
- эллипс  Ответ.
Ответ. 
3. С помощью криволинейных интегралов вычислить площади областей, ограниченных следующими кривыми:
а)  (эллипс). Ответ.
(эллипс). Ответ. 
б)  и
и
 (парабола)
(парабола)
Ответ. 

в)  (петля декартова листа).
(петля декартова листа).
Ответ.  .
.