5.1. Распределенные параметры
Цепью с распределенными параметрами называют электромагнитное устройство, геометрические размеры которого соизмеримы с длиной волны 
электромагнитных колебаний.
В вакууме величина определяется частотой сигнала
, 
- скорость света.
Удобно использовать выражение
.
Если с длиной волны соизмерима только длина устройства (например, тракта передачи сигнала – фидера), а остальные размеры много меньше 
, то его называют длинной линией.
В дальнейшем будем рассматривать длинные линии.
При 
получим 
, и если длина фидера больше 1 м, то он является длинной линией, а если она равна 10 см, то фидер можно рассматривать просто как соединительный проводник.
Примеры конструкций двухпроводной длинной линии и коаксиального кабеля показаны на рис. 5.1а и рис. 5.1б соответственно.
Рис. 5.1
Представим длинную линию как каскадное соединение бесконечно малых ее отрезков длиной 
, эквивалентная схема показана на рис. 5.2.
Каждый отрезок можно представить показанной ниже эквивалентной схемой, в которой присутствуют бесконечно малые индуктивность линии 
, сопротивление потерь, емкость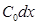 
и проводимость утечки 
. Величины 
(Гн/м),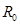 
(Ом/м), 
(Ф/м) и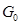 
(Сим/м) называют погонными параметрами длинной линии.
Рис. 5.2
5.2. Телеграфные уравнения
Каждый отрезок длинной линии в точке 
от начала координат функций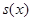 
или в точке 
от начала координат функций 
(
, 
- длина линии, 
- ток или напряжение) можно представить показанной ниже эквивалентной схемой, в которой можно обозначить мгновенные значения входных и выходных токов и напряжений, как показано на рис. 5.3.
Рис. 5.3
По первому закону Кирхгофа
|
|
,
тогда
,
и в результате
.
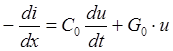По второму закону Кирхгофа
,
тогда
,
.
Телеграфные уравнения длинной линии имеют вид
Ток и напряжение являются функциями двух переменных
и 
,
тогда
Для гармонических сигналов целесообразно ввести комплексные амплитуды тока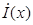 
и напряжения 
как показано в схеме на рис. 5.4.
Рис. 5.4
Тогда получим
тогда
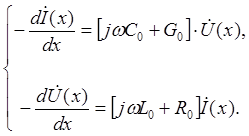или 
Подставляя одно уравнение в другое, получим
где
.
Комплексную величину 
называют постоянной распространения длинной линии, 
- коэффициент затухания волны в линии, а 
- коэффициент фазы
,
В линии без потерь (при 
и 
) получим
,
тогда
5.3. Решение телеграфных уравнений
Для телеграфных дифференциальных уравнений для комплексных амплитуд тока и напряжения в длинной линии вида
получим характеристическое уравнение вида
,
а его корни равны
Общее решение для напряжения имеет вид
.
Используя уравнение
,
получим
.
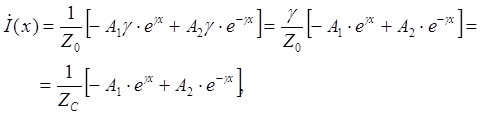где с учетом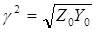 
- комплексное волновое сопротивление длинной линии. Для линии без потерь волновое сопротивление активно и равно
.
Для стандартных фидеров – коаксиальных кабелей волновое сопротивление равно 50 Ом или 75 Ом.
Постоянные интегрирования 
и 
определяются их начальных условий, в качестве которых используются значения тока и напряжения в начале (
) или чаще всего в конце (
) линии.
Пусть заданы в конце линии (в точке 
), тогда
.
Решая систему уравнений (складывая и вычитая уравнения), найдем постоянные интегрирования
|
|
и получим
где
По комплексным амплитудам тока и напряжения найдем их мгновенные значения
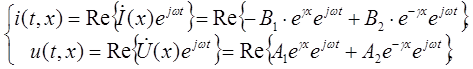
тогда
Аналогично для тока провести расчет самостоятельно.
5.4. Отраженная и падающая волны
В теории волновых процессов рассматривается гармоническая функция двух аргументов, например, волна напряжения
Под движением волны понимают перемещение в пространстве (по оси 
) точки фиксированной фазы волны
.
Скорость ее движения 
называют фазовой скоростью волны. Продифференцируем ее по времени, тогда
Фазовая скорость равна
.
Направление распространения волны – от источника к нагрузке и эту волну называют падающей.
Другую часть волнового процесса называют отраженной волной,
,
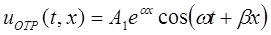так как ее фазовая скорость
.
отрицательна (получите результат самостоятельно) и волна распространяется от нагрузки к источнику. Направления распространения этих волн показаны на рис. 5.5, а пространственные диаграммы их амплитуд – на рис. 5.6.
Рис. 5.5.
Рис. 5.6.
Как видно, падающая и отраженная волны затухают по направлению распространения, затухание определяется коэффициентом затухания 
.
При отсутствии потерь 
.
Длина волны 
- расстояние между точками с одинаковой фазой (рис. 5.6). Фаза в точке 
равна 
, а в точке 
соответственно 
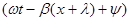, а их разность равна 
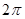, тогда получим
,
в результате коэффициент фазы связан с длиной волны колебаний l в линии выражением
5.5. Коэффициент отражения
Комплексные амплитуды падающей и отраженной волн равны
|
|
Комплексные коэффициенты отражения по напряжению и току равны
,
.
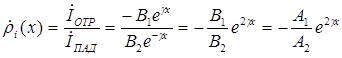Ранее исходя из начальных условий в конце линии были определены постоянные интегрирования
Тогда для коэффициентов отражения получим
,
.
Модули коэффициентов отражения одинаковы и равны отношению амплитуд отраженной волны к падающей,
.
На конце линии (пр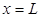и 
или 
) модуль коэффициента отражения равен
.
При удалении от нагрузки модуль коэффициента отражения падает.
Как видно, имеется особое значение сопротивления нагрузки
при котором коэффициент отражения равен нулю во всех точках линии.
5.6. Режимы работы длинной линии
5.6.1. Режим бегущих волн
В режиме бегущих волн в линии присутствует только падающая волна напряжения или тока. Он возникает в линии с согласованной нагрузкой
.
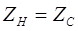Коэффициент отражения и амплитуда отраженной волны равны нулю во всех точках линии. Комплексные амплитуды падающей волны равны
.
При 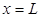получим
, 
Для амплитуд получим
.
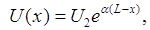
Графики для амплитуды напряжения показаны на рис. 5.7.
Рис. 5.7
В линии без потерь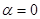 
и
.
В режиме бегущих волн отражения отсутствуют и мощность полностью передается от источника к нагрузке.
Режим бегущих волн используется для передачи сигнала от источника к нагрузке. Передающую длинную линию называют фидером.
5.6.2. Режим стоячих волн в линии без потерь
При отсутствии потерь
Эти выражения приближенно справедливы и в длинной линии с потерями при условии R0 << wL0, G0 << wC0.
Режим стоячих волн возникает, когда модуль коэффициента отражения равен 1 и ,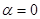
.
Он возникает при следующих нагрузках:
- короткое замыкание (
);
- холостой ход (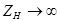
);
- реактивная нагрузка (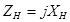
).
В режиме стоячих волн амплитуда отраженной волны равна амплитуде падающей.
В общем случае при 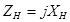получим
.
Для комплексных амплитуд напряжения и тока получим
,
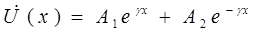где
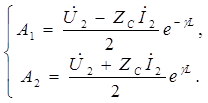
Тогда получим
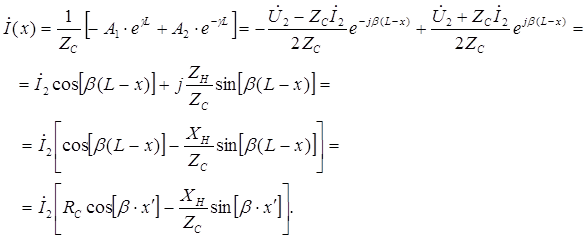
Рассмотрим короткое замыкание (), тогда 
получим
,
а для амплитуд
,
.
Зависимости амплитуд тока и напряжения показаны на рис. 5.8.
Рис. 5.8
Как видно, на нагрузке имеется максимум (пучность) тока и ноль (узел) напряжения. При удалении от нагрузки ток падает, а напряжение растет, и при
или 
имеется узел тока и пучность напряжения.
В общем случае для напряжения узлы расположены на расстоянии
а пучности при
.
Для тока положение узлов и пучностей противоположно.
При холостом ходе нагрузки ()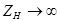 
, тогда аналогично предыдущему получим
,
.
Зависимости амплитуд тока и напряжения показаны на рис. 5.9.
Рис. 5.9
Положение узлов и пучностей противоположно предыдущему.
5.6.3. Линия без потерь при реактивной нагрузке
Решение телеграфных уравнений имеет вид
,
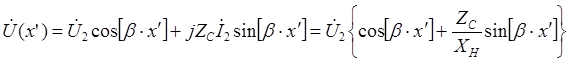Рассмотрим напряжение в линии (ток проанализируйте самостоятельно):
,
.
Для амплитуды получим
,
Зависимости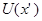 
показаны на рис. 5.10.
Рис. 5.10
Как видно, при подключении реактивной нагрузки происходит смещение узлов и пучностей тока и напряжения. На рис. 5.10а показана зависимость 
для разомкнутой на конце линии. При подключении к линии емкостной нагрузки (рис. 5.10б)
с отрицательным реактивным сопро-тивлением происхо-дит смещение узлов и пучностей в сторону генератора (
). При этом линия как будто становится короче (укорочение длин-ной линии), как по-
Рис. 5.11 казано на рис. 5.11.
Аналогично, при подключении к разомкнутой диной линии индуктивности происходит ее удлинение (рис. 5.10в).
Смещение узлов и пучностей можно использовать для измерения неизвестных индуктивностей и емкостей. Например, если при подключенной емкости 
к разомкнутой длинной линии узел напряжения сместился к источнику на величину 
, то значение емкости определится из уравнения
,
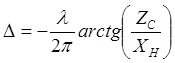тогда
или 
.
Если в короткозамкнутой линии вместо замыкателя подключить индуктивность L, то узлы и пучности сместятся ближе к нагрузке на расстояние
Полученное выражение следует из того, что индуктивность L можно заменить отрезком короткозамкнутой линии длиной 
.
5.6.4. Линия без потерь при несогласованной активной нагрузке
Рассмотрим напряжение в линии при несогласованной активной нагрузке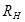 
,
,
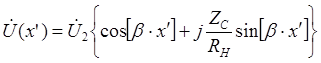тогда для амплитуды (модуля) получим при 
При 
получим 
, как это имеет место в режиме бегущих волн. Зависимости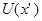 
для различных 
показаны на рис. 5.12.
Рис. 5.12
Как видно из рис. 5.12, при несогласованном режиме работы длинной линии имеют место и падающая и отраженная волны.
5.7. КСВ и КБВ
Соотношение между амплитудами стоячей и бегущей волн в длинной линии характеризуется коэффициентом бегущей волны (КБВ)
или коэффициентом стоячей волны (КСВ)
где Umin и Umax - соответственно наименьшая и наибольшая амплитуды напряжения вдоль линии. На рис. 5.12 КБВ=0,5, а КСВ=2.
В длинной линии без потерь при активной нагрузке Rн можно записать
Эти коэффициенты легко измеряются, тогда, зная волновое сопротивление линии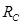 
, можно измерять активное сопротивление неизвестной нагрузки.
Величина КСВ широко используется как мера близости режима работы линии к согласованному.
5.8. Входное сопротивление линии
Входное сопротивление Zвх линии в этом случае определяется выражением т(получите его самостоятельно)
При Rн=Zс (в режиме бегущих волн) входное сопротивление линии равно характеристическому Zвх=Zс, а, например, при коротком замыкании линии (Rн=0) входное сопротивление реактивно и равно
.
Зависимость 
от 
показана на рис. 5.13.
Рис. 5.13
Как видно, по мере удаления от короткозамкнутой нагрузки входное сопротивление линии без потерь становится сначала индуктивным, потом емкостным и т.д.
Волновое сопротивление двухпроводной длинной линии, размещенной в вакууме (в воздухе) активно и равно
где d - радиус проводов линии, D - расстояние между центрами проводов линии.
5.9. Применение длинной линии
5.9.1. Фидер
Фидер предназначен для передачи сигнала от источника в нагрузку (рис. 5.14).
Рис. 5.14
Если длина фидера 
соизмерима с длиной волны 
, то он является длинной линией.
,
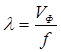где 
- фазовая скорость, в вакууме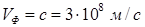 
- скорость света.
В длинной линии присутствуют потери мощности сигнала и его уровень падает при удалении от источника,
,
- коэффициент затухания с размерностью 1/м, часто используется размерность Дб/м. Зависимость 
показана на рис. 5.15
Рис. 5.15
Например, если в коаксиальном кабеле затухание равно 
=0,1 Дб/м, то для фидера длиной L=100 м затухание сигнала составит 10 Дб или 10 раз по мощности, а по напряжению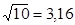 
раза. Чем длиннее фидер, тем выше затухание.
5.9.2. Отрезок длинной линии
Отрезок разомкнутой на конце длинной линии длиной 
имеет емкостное сопротивление, равное
,
Зависимость 
от 
показана на рис. 5.16.
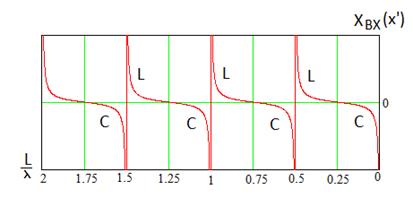
Рис. 5.16
Как видно, с его помощью можно реализовать любое реактивное сопротивление (индуктивное или емкостное). Для емкостного сопротивления чаще всего используют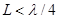 
, а для индуктивного применяют короткозамкнутый отрезок линии.
Разомкнутый на конце отрезок линия при
ведет себя как последовательный колебательный контур, а при
- как параллельный. Для короткозамкнутого отрезка эти формулы меняются местами.
Короткозамкнутый отрезок линии без потерь длиной
имеет бесконечное входное сопротивление и используется как крепежная подставка для двухпроводной линии (рис. 5.17).
Рис. 5.17
5.9.3. Четвертьволновый трансформатор
Отрезок линии длиной
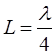
с волновым сопротивлением 
можно использовать для трансформации сопротивления нагрузки фидера с целью обеспечения в нем режима бегущих волн, как показано на рис. 5.18.
Рис. 5.18
При отсутствии потерь для четвертьволнового отрезка получим
,
и это сопротивление должно быть равно волновому сопротивлению фидера
,
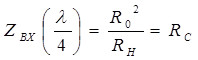тогда волновое сопротивление четвертьволнового трансформатора должно быть равно
5.9.4. Согласующий шлейф
Если нагрузка линии не согласована (
), то для обеспечения режима бегущих волн в основной части фидера используют согласование шлейфом, как показано на рис. 5.19.
Рис. 5.19
В точках подключения фидера ab входная проводимость его отрезка с нагрузкой должна быть равна
,
где 
- получившаяся реактивная входная проводимость. Из уравнения
найдем величину 
, а реактивная проводимость будет равна
.
Для ее компенсации и используется шлейф, реактивная проводимость которого должна быть равна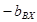 
.
Для короткозамкнутого шлейфа
,
тогда из уравнения
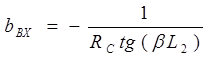
найдем длину шлейфа 
.
Пример программы расчета шлейфа показан на рис. 5.20. Как видно, при 
Ом и 
Ом нагрузка не согласована. На расстоянии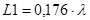 
от нее активная составляющая проводимости равна 
Сим и имеет емкостный характер (
). Тогда шлейф должен иметь индуктивный характер проводимости, равный 
Сим, что имеет мести на расстоянии 
от короткого замыкания. В этом случае в основной части фидера реализуется режим бегущих волн, от точек подключения шлейфа до нагрузки – режим смешанных волн, а в шлейфе – режим стоячих волн.
