Раздел 6. Уравнения и неравенства.
Тема1. Решение уравнений.
Уравнение – это равенство с переменной.
Решить уравнение – значит найти его корни или доказать что их нет.
Корень уравнения – это значение переменной, при подстановки которого уравнение обращается в верное равенство.
Уравнения, имеющие одно и тоже множество корней называются равносильными.
Пример1: (х – 2) (х +4)= 0 и 3х – 6 = 0
Корни: х1 = 2, х 2= - 4 и х = 2.
Вывод: уравнения не равносильные.
Пример 2. Уравнения Х 2 = -9 и 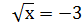 не имеют корней, следовательно они равносильны.
не имеют корней, следовательно они равносильны.
Чтобы проверить равносильность уравнения, надо найти их корни и сравнить.
Равносильность сохраняется при:
· Тождественных преобразованиях (раскрытие скобок, приведение подобных….)
· При умножении и делении обеих частей уравнения на число,
неравное 0.
· При переносе слагаемых из одной части уравнения в другую, меняя при этом знак на противоположный.
Посторонний корень может быть:
· При умножении обеих частей уравнения на выражение с переменной
· При возведении обеих частей уравнения в чётную степень.
Потеря корня может быть при делении обеих частей уравнения на выражение с переменной
| Вид уравнения | Алгоритм решения | Пример |
| Линейное | 1) Перенос слагаемых из одной части уравнения в другую. 2) нахождение неизвестного компонента | 3х – 7 = 5х + 5 Решение: 3х – 5х = 5 + 7 -2х = 12 х = 12: (-2) х = -6. Ответ: - 6. |
| Дробное | 1) Найти ОДЗ 2) Найти общий знаменатель 3) Найти дополнительный множитель к каждой дроби 4) «Отбросить» знаменатель и решить получившееся уравнение 5) Выполнить проверку |  Решение: ОДЗ:
Решение: ОДЗ: 



 или или  х = 0 или х = 1 – посторонний корень (см ОДЗ).
Ответ: х = 0.
х = 0 или х = 1 – посторонний корень (см ОДЗ).
Ответ: х = 0.
|
Квадратное
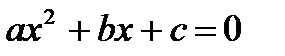
|  , ( , ( ) )
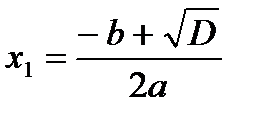 
|  .
Решение: .
Решение: 

 Ответ: 5 и -1.
Ответ: 5 и -1.
|
Неполное квадратное
(если с = 0)

| 
 или или 

|  .
Решение: .
Решение:
 3х = 0 или 2х – 1 = 0
х = 0 или 2х = 1
3х = 0 или 2х – 1 = 0
х = 0 или 2х = 1  .
Ответ: 0 и 0,5. .
Ответ: 0 и 0,5.
|
Неполное квадратное
(если b = 0)

| 


|  Решение:
Решение:


 Ответ:
Ответ: 
|
Задание 1. Равносильны ли следующие уравнения:
А) х (х-6) + 10 = 1 и 2(х + 4) = 14 б) 1 + х (х – 4) = - 3 и 3(х – 1) = 3
Задание 2.
(Из учебника, стр 295): № 130 (в), № 131 (в), № 136 (в), № 140 (в).
Тема 2. Решение неравенств.
| неравенства | знаки | Точка | Скобки |
| строгие | < или > | 
| () |
| нестрогие |  или или 
| 
|

|
Неравенства, имеющие одно и тоже множество решений, называются равносильными.
Пример 1. Равносильны ли неравенства: 2х > 10 и -3х < -15.
Решаем первое неравенство: х >5, решаем второе неравенство: х > 5 (знак неравенства меняется при делении или умножении на отрицательное число).
Вывод: неравенства равносильные.
| Вид неравенства | Алгоритм решения | Пример | ||||||
| Линейное | Перенос слагаемых из одной части неравенства в другую |  Решение:
Решение:


 . Знак неравенства меняется при делении на отрицательное число!
-11
Ответ: . Знак неравенства меняется при делении на отрицательное число!
-11
Ответ:  
| ||||||
| Дробное Квадратное | Метод интервалов: 1)Найти ОДЗ 2)ввести функцию у = f(x) 3)f(x)=0 4)корни уравнения и точки исключения (см. ОДЗ) отметить на прямой и разбить на интервалы 5)Найти знак в каждом интервале (подставить удобное число в функцию) 6)Выбрать «нужные» промежутки (см. знак неравенства) | 1)  Решение: ОДЗ: R.
Рассмотрим функцию
Решение: ОДЗ: R.
Рассмотрим функцию 
 , ,  0,5 1
0,5 1
Ответ: 2) Решение: ОДЗ:
-2 0
Ответ: (-2; 0) |
Задание 1. Равносильны ли следующие неравенства:
А) (х – 2)(х + 4) < х (х +9) и 2х + 4 < -5х – 4
Б) х (х+8) > (х +3)(х – 2) и 2х – 9 > 9х – 3.
Задание 2.
(Из учебника, стр 295): № 133 (в), № 142 (в), № 143 (в)
Тема 3. Решение систем уравнения
Метод сложения: 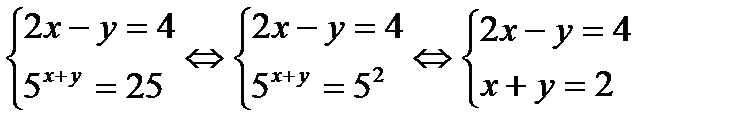 .
.
Сложим первое и второе уравнения, получим:  . Ответ: (2; 0).
. Ответ: (2; 0).
Метод подстановки: 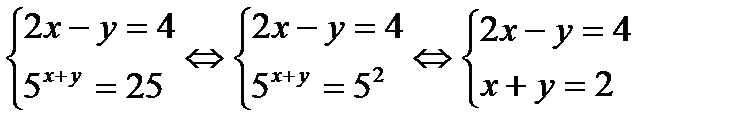 .
.
Выразим у из второго уравнения и подставим в первое, получим:  . Ответ: (2; 0).
. Ответ: (2; 0).
Графический метод:  .
.
Решение: 1) Построим график функции  - показательная функция
- показательная функция
| х | -2 | -1 | |||
| у | 
| 
|
| х | ||
| у | -1 |
2) Построим график функции у = 1 – 2х – линейная функция
| -2 |
| -1 |
| ,1 |
| 3,5 |
| - |
| -3 |
| -2 |
| -1 |
Решением системы является точка пересечения графиков.
Ответ: (0; 1).
Задание 1. (Из учебника, стр 301): № 180.




 . Функция:
. Функция: 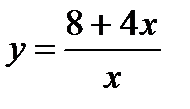 ,
, 
