Нахождение производных и нахождение неопределенных интегралов
(дифференцирование и интегрирование) – это два взаимно обратных действия,
как, например, сложение/вычитание или умножение/деление]

1. Понятие неопределенного интеграла
Опр. 1. Функция  называется первообразной функции
называется первообразной функции  на интервале (a; b), если в любой точке этого интервала верно равенство:
на интервале (a; b), если в любой точке этого интервала верно равенство:
 .
.
Первообразных для одной и той же функции может быть бесконечно много, c точностью до константы С - числа, т.к.  .
.
Опр. 2. Неопределенным интегралом функции f (x) называется множество всех ее первообразных функций F (x) + C. Обозначается:
 .
.
Здесь f (x) называется подынтегральной функцией,  – подынтегральным выражением,
– подынтегральным выражением,
х – переменной интегрирования,  – знаком неопределенного интеграла.
– знаком неопределенного интеграла.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
2. Таблица неопределенных интегралов
Посмотрим в таблицу интегралов.
Что происходит? Левые части  у нас превращаются в другие функции (справа):
у нас превращаются в другие функции (справа):  .
.
Тогда:
Найти неопределенный интеграл  – это значит ПРЕВРАТИТЬ его в определенную функцию
– это значит ПРЕВРАТИТЬ его в определенную функцию  , пользуясь некоторыми правилами, приемами и таблицей.
, пользуясь некоторыми правилами, приемами и таблицей.
Возьмем, например, табличный интеграл 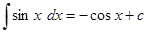 . Что произошло?
. Что произошло?  превратился в функцию
превратился в функцию  .
.
Как и в случае с производными, для того, чтобы научиться находить интегралы по таблице, не обязательно быть в курсе, что такое интеграл, первообразная функция с теоретической точки зрения. Достаточно просто осуществлять превращения по некоторым формальным правилам. Так, в случае 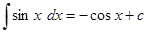 совсем не обязательно понимать, почему интеграл
совсем не обязательно понимать, почему интеграл  превращается именно в
превращается именно в  . Пока можно принять эту и другие формулы как данность. Все пользуются электричеством, но мало кто задумывается, как там по проводам бегают электроны [1]:))).
. Пока можно принять эту и другие формулы как данность. Все пользуются электричеством, но мало кто задумывается, как там по проводам бегают электроны [1]:))).
Таблица интегралов
1.  2.
2.  3.
3.  частные случаи:
3а)
частные случаи:
3а)  ,
3б) ,
3б) 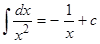 .
4а) .
4а)  4в)
4в)  5а)
5а)  6)
6) 
| обобщенные интегралы
9)  10)
10)  11)
11)  12)
12)  4б)
4б) 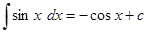 4г)
4г)  5б)
5б) 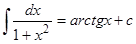 7)
7)  8)
8) 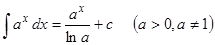
|
Если продифференцировать правильный ответ, то обязательно должна получиться исходная подынтегральная функция, смотрите:




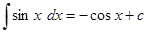

 + с
+ с
А значит,
 .
.
3. Свойства неопределенного интеграла. Методы интегрирования. Примеры нахождения интегралов
1. Постоянный множитель (числовой) можно выносить за знак интеграла: 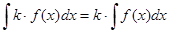 , где постоянная
, где постоянная  .
.
2. Неопределенный интеграл от суммы конечного числа функций равен сумме интегралов от слагаемых функций:  , где u, v, w – некоторые функции от х.
, где u, v, w – некоторые функции от х.
Примеры. Найдите интегралы:
а)  ; б)
; б)  .
.
Решение: а)
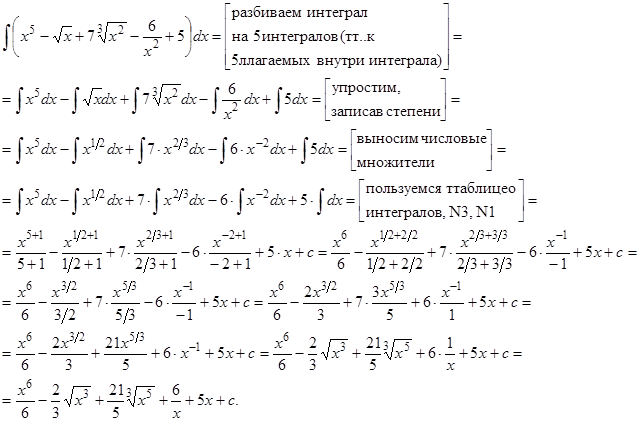
 Ответ:
Ответ:  .
.
Применяли правило  . Не забывали записать значок дифференциала
. Не забывали записать значок дифференциала  в каждом интеграле. Почему в каждом
в каждом интеграле. Почему в каждом  ? – это полноценный множитель при раскрытии скобки. Кстати, константу С достаточно приплюсовать один раз в конце выражения (а не ставить их после каждого интеграла).
? – это полноценный множитель при раскрытии скобки. Кстати, константу С достаточно приплюсовать один раз в конце выражения (а не ставить их после каждого интеграла).
б)

Ответ: 
3. Основные методы интегрирования
Непосредственное интегрирование
Метод интегрирования, при котором интеграл с помощью свойств неопределенного интеграла и тождественных преобразований подынтегральной функции приводится к табличным интегралам, называется непосредственным интегрированием.
Примеры:
а) Деление многочлена, стоящего в числителе, на знаменатель.

 .
.
б) Использование формул тригонометрии.
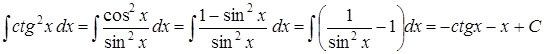 .
.
в) 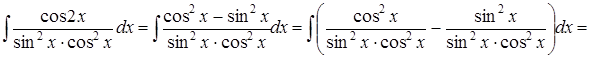
 .
.
г) Приведение подынтегральной функции к табличным интегралам.

 .
.
д) 
 .
.
8) 
