ВСЕРОССИЙСКИЙ ДЕТСКИЙ КОНКУРС
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИХ И ТВОРЧЕСКИХ РАБОТ
«ПЕРВЫЕ ШАГИ В НАУКЕ»
Секция: информационные технологии, математика
Тема: Исследование свойств целых чисел позиционных систем счисления
Автор: Лагутин Андрей Дмитриевич
Научный руководитель: Бородулина Инга Рудольфовна
Место выполнения работы: МБОУ СОШ №1, Астраханская обл., г. Ахтубинск
Исследование свойств целых чисел позиционных систем счисления
Введение
В ходе изучения курса математики в начальной школе у учеников формируется навык счета по десяткам. Этому способствует физиологическая особенность человека, ведь у него на руках десять пальцев. Изучение чисел второго десятка происходит путем запоминания, без системы. Однако, у ребенка есть понимание, что он имеет дело с числами от 10 до 20, то есть со вторым десятком. После овладения методами работы с первыми двумя десятками чисел, у ребенка формируется правило работы с любыми числами от 1 до 100. Расширяя правило работы с числами в десятичной системе счисления, ребенок способен работать и с большими числами по правилам, без использования механизма запоминания.
Таким образом, в настоящее время десятичная система счисления для детей выглядит естественной, по ощущениям – единственно правильной.
Однако, когда я начал осваивать программирование микроконтроллеров, а также прикладное программирование, в литературе встречались ссылки на шестнадцатеричные, восьмеричные и двоичные целые числа.
Понимание сути данных чисел для школьника, изучающего программирование (особенно программирование микроконтроллеров) является актуальной и необходимой задачей.
В данной работе мною выполнено исследование свойств целых чисел различных позиционных систем счисления, при этом каждый разряд числа рассматривался как система, имеющая определенное число состояний.
В качестве методов исследования используются эксперимент, физическое моделирование и обобщение.
Определение количества состояний числа в каждом разряде
Для определения количества состояний числа в каждом разряде проведена серия экспериментов с адаптированными счетами. Адаптированные счеты выполнены специальным образом, со сменным количеством косточек. Перед исследованием очередной системы счисления руководитель проекта изменял количество косточек на каждом уровне счет, сообразно свойствам рассматриваемой системы счисления. Данная серия экспериментов начиналась с использования классических «десятичных» счет (рисунок 1).
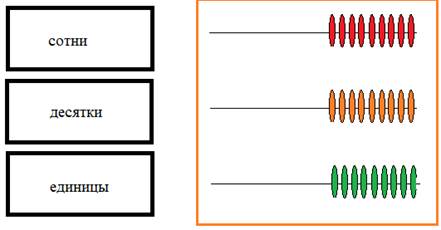
Рисунок 1
Попытаемся узнать, сколько возможно различных вариантов для установки косточек в разряде единиц в крайне левом положении. Эксперимент показывает, что возможно установить в крайне левом положении:
1. ноль косточек;
2. одну косточку;
3. две косточки;
…
9. восемь косточек;
10. девять косточек.
Итак, количество возможных вариантов установки косточек в крайнем левом положении в разряде единиц равно 10 (далее, количество возможных состояний). Так как количество косточек в каждом разряде одинаково, то данный вывод распространяется для всех разрядов данной системы счисления. Кроме того, это подтверждено опытным путем, аналогично предыдущему эксперименту.
Вывод: в десятичной системе счисления количество возможных состояний для каждого разряда равно 10.
Для определения свойств восьмеричной системы счисления проводились эксперименты, используя адаптированные «восьмеричные» счеты (рис.2). Эксперименты выполнялись аналогично ранее описанному. Счеты содержат три разряда. В результате экспериментов получено, что количество возможных состояний в младшем, среднем и старшем разрядах равно 8.

Рисунок 2
Далее, на адаптированных «шестнадцатеричных» счетах (см. рисунок 3) исследовались свойства шестнадцатеричной системы счисления. Эксперименты выполнялись аналогично ранее описанным. Счеты содержат три разряда. В результате экспериментов получено, что количество возможных состояний в младшем, среднем и старшем разрядах равно 16.
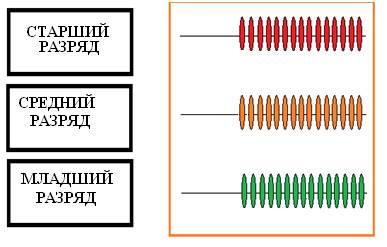
Рисунок 3
Путем обобщения полученных результатов сделан вывод, что количество состояний в каждом разряде целого числа позиционной системы счисления равно основанию системы счисления.