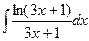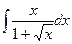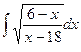Задачи для подготовки к экзамену по курсу «Интегральное исчисление и ДУ»
ИНМиН, 2015-16 учебный год
Неопределенный интеграл
Определенный интеграл
- Вычислить
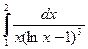 . Существует ли аналогичный интеграл по отрезку [1; 3]?
. Существует ли аналогичный интеграл по отрезку [1; 3]? - Вычислить
 .
. - Вычислить
 .
. - Вычислить
 .
. - Вычислить

- Вычислить
 .
. - Вычислить

- Вычислить

- Вычислить

- Вычислить
 .
. - Вычислить
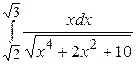
- Вычислить
 .
. - Выяснить, не вычисляя, какой интеграл больше,
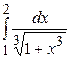 или
или  ?
? - Найти среднее значение функции f (x) = sin2 x на отрезке [0,p].
- Найти производную функции F (x)=
 .
. - Найти длину дуги кривой, заданной уравнением
 .
. - Найти длину дуги линии, заданной функцией у = е х + 3, ln2 £ x £ ln5.
- Найти длину дуги кривой, заданной уравнением у =
 , 0 £ х £ 8/9.
, 0 £ х £ 8/9.
Несобственные интегралы
- Вычислить несобственный интеграл
 или доказать его расходимость.
или доказать его расходимость. - Вычислить несобственный интеграл
 или доказать его расходимость.
или доказать его расходимость. - Вычислить несобственный интеграл
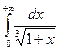 или доказать его расходимость.
или доказать его расходимость. - Вычислить
 или доказать его расходимость
или доказать его расходимость - Исследовать на сходимость
 .
. - Исследовать на сходимость
 .
. - Исследовать на сходимость
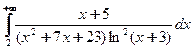 .
. - Исследовать на сходимость
 .
. - Исследовать на сходимость
 .
. - Исследовать на сходимость.
 .
. - Исследовать на сходимость
 .
. - Исследовать на сходимость
 .
. - Исследовать на сходимость
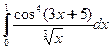 .
. - Исследовать на сходимость
 .
. - Исследовать на сходимость в зависимости от параметра a интеграл
 .
.
Дифференциальные уравнения
- Найти общее решение ДУ:
 .
. - Найти общее решение ДУ: (ex +1) y ' = y ex.
- Решить задачу Коши: 2(1 + e x) yy ' = e x,
 .
. - Решить задачу Коши: (1 + e x) yy' = e x, y (0) =
 .
. - Решить задачу Коши:

- Решить задачу Коши: y' = – 2 xу 2, y (0) = 1
- Решить задачу Коши: y ' + 2 xy = – 2 x 3, y(1) = е – 1.
- Решить задачу Коши: y ' - 2 y / х = x 2, y (1) = 2.
- Решить задачу Коши: y' – x 2 y = x 2, y (0) = 0.
- Решить задачу Коши: y ' + y cos x = 0,5sin2 x, y (0) = 0.
- Решить задачу Коши:
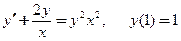 .
. - Решить задачу Коши: y' + xy = (1+ x)e – x y 2, y (0) = 1.
- Решить задачу Коши: y '– y = x y2, y (0) = 1.
- Решить задачу Коши: xy' + y = xy 2, y (1) = 1.
- Решить задачу Коши: xy' + y ln y = 0, y (1) = e.
- Решить задачу Коши: y' = x (y – 1), y (1) = 1/2.
- Решить задачу Коши:

- Решить задачу Коши: y' = y e x /(e x + 3), y (0) = 1.
- Решить задачу Коши: xy' = y ln(y/x), у (1) = 1.
- Найти общее решение ДУ: y'' – 2 y' + 5 y = 0.
- Найти общее решение ДУ: у '' + 7 y ' + 6 y = 0.
- Найти общее решение ДУ: у '' – 3 y ' - 4 y = 0.
- Найти общее решение ДУ: у ¢¢¢ - 5 y ¢¢ + 6 y ¢ = 0.
- Найти общее решение ДУ: у''' + 25 y' = 0.
- Найти общее решение ДУ у'' – 2 y' + 10 y = 0.
- Найти общее решение ДУ: у'' + 8 y' + 16 y = 0.
- Найти общее решение ДУ: у ¢¢ + 5 y ¢ - 6 у = 0.
- Найти общее решение ДУ: y ¢¢ + 4 y = 0.
- Найти общее решение ДУ: у'' – 8 y' + 16 y = 0.
- Решить задачу Коши: y '' + 6 y ' + 9 y = 0, y (0) = 0, y ¢(0) = 1.
- Решить задачу Коши: у '' + 16 y = 32 х, у (0) = 0, y '(0) = 6.
- Решить задачу Коши: у ¢¢¢+ 9 y ¢ = е х, у (0) = 0, y' (0) = 1, y'' (0) = 1
- Решить задачу Коши:
 ,
,  ,
, 
- Решить задачу Коши:
 .
. - Найти общее решение ДУ: у ''' + 9 y ' = 9 х + 54e3x.
- Найти общее решение ДУ у ¢¢¢ – 4 y ¢¢ + 8 y' = е–2 х .
- Найти общее решение ДУ: у''' + y' = 4 х + 10 е 2 х + cos2 x.
- Найти общее решение ДУ: y ''' + 4 y ' = 3 + е – x +sin3 x.
- Найти общее решение ДУ: у''' – y' = 5 + 2e x + cos x.
- Решить задачу Коши: y¢¢ + y = 1/ sin x, y (p/2) = 1, y¢ (p/2)= p/2.
- Решить задачу Коши: x 2 у'' + x y' = 1, y (1) = y ' (1) = 0.
- Решить задачу Коши: y '' у 3 + 1= 0, y (1) = – 1, y ' (1) = –1.
- Решить задачу Коши: 4 у 3 y'' = у 4 –1, y (0) =
 , y' (0) =
, y' (0) =  .
. - Решить задачу Коши: y'' = 50у3, y(3) = 1, y '(3) = 5.
- Решить задачу Коши для системы ДУ:
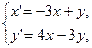 x (0) = 4, y (0) = 0. Определить тип положения равновесия системы и построить фазовые траектории.
x (0) = 4, y (0) = 0. Определить тип положения равновесия системы и построить фазовые траектории. - Решить задачу Коши для системы ДУ:
 x (p) = 1, y (p) = 0. Определить тип положения равновесия системы и построить фазовые траектории.
x (p) = 1, y (p) = 0. Определить тип положения равновесия системы и построить фазовые траектории. - Решить задачу Коши для системы ДУ:
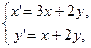 , x (0) = 0, y (0) = 2. Определить тип положения равновесия системы и построить фазовые траектории.
, x (0) = 0, y (0) = 2. Определить тип положения равновесия системы и построить фазовые траектории. - Определить тип положения равновесия и нарисовать фазовые траектории системы
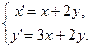
Найти общее решение системы.
- Определить тип положения равновесия и нарисовать фазовые траектории системы
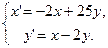 Найти общее решение системы.
Найти общее решение системы. - Определить тип положения равновесия и нарисовать фазовые траектории системы

Найти общее решение системы.
- Определить тип положения равновесия и нарисовать фазовые траектории системы
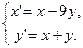
Найти общее решение системы.
- Определить тип положения равновесия и нарисовать фазовые траектории системы

Найти общее решение системы.
- Определить тип положения равновесия и нарисовать фазовые траектории системы

Найти общее решение системы.
- Определить тип положения равновесия и нарисовать фазовые траектории системы
 Найти общее решение системы.
Найти общее решение системы. - Определить тип положения равновесия и нарисовать фазовые траектории системы
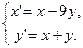
Найти общее решение системы.
- Определить тип положения равновесия и нарисовать фазовые траектории системы
 Найти общее решение системы.
Найти общее решение системы.
Кратные интегралы
- Вычислить
 , если область G – треугольник с вершинами в точках А (0, 0), В (3, 3), С (3, 1).
, если область G – треугольник с вершинами в точках А (0, 0), В (3, 3), С (3, 1). - Вычислить
 , где G - область, ограниченная линиями y = 4 – x 2, y = x + 2.
, где G - область, ограниченная линиями y = 4 – x 2, y = x + 2. - Вычислить интеграл
 , если G – область, ограниченная линиями y = x 2 – 4, y = x +2.
, если G – область, ограниченная линиями y = x 2 – 4, y = x +2. - Вычислить
 , если G – область, ограниченная линиями: y = x, y = 2 – x, у = 0.
, если G – область, ограниченная линиями: y = x, y = 2 – x, у = 0. - Вычислить
 , если G – область, ограниченная линиями: y = x +1, y = 1 – x, у = 0.
, если G – область, ограниченная линиями: y = x +1, y = 1 – x, у = 0. - Вычислить
 , где G – область, ограниченная линиями y = x, y = 2 x, х = 1.
, где G – область, ограниченная линиями y = x, y = 2 x, х = 1. - Вычислить интеграл
 , если G – область, ограниченная линиями x =1, y = x 3, у = –
, если G – область, ограниченная линиями x =1, y = x 3, у = –  .
. - Вычислить интеграл
 , если область G – четырехугольник с вершинами в точках А (0,0), В (0,3), С (2,5), D (2,2).
, если область G – четырехугольник с вершинами в точках А (0,0), В (0,3), С (2,5), D (2,2). - Вычислить интеграл
 , если G – область, ограниченная линиями y = x, y = 2 x, y =2.
, если G – область, ограниченная линиями y = x, y = 2 x, y =2. - Вычислить интеграл
 , предварительно изменив порядок интегрирования.
, предварительно изменив порядок интегрирования.
- Вычислить
 , где G = {(x, y): x 2+ y 2 £ 4 y, x ³ 0 }.
, где G = {(x, y): x 2+ y 2 £ 4 y, x ³ 0 }. - Вычислить
 , где G ={(x, y): x 2 + y 2 £ 2 y }.
, где G ={(x, y): x 2 + y 2 £ 2 y }. - Вычислить площадь фигуры, ограниченной линиями у = х 2 – 5, у = 4 х.
- Вычислить площадь фигуры, ограниченной линиями y = x 2 – 1, y = x + 1.
- Найти площадь фигуры, ограниченной линиями x = y 2 – 1, y = 1 – x.
- Вычислить площадь фигуры, ограниченной линиями у = 32 – х 2, у = – 4 х.
- Вычислить площадь фигуры, ограниченной линиями x 2 – 4 х + y 2 = 0, x 2 – 2 х + y 2 = 0, у = 0, у = х.
- Пластинка задана ограничивающими ее кривыми: х = 2, у = 0, у 2 = х /2 (у ³ 0). Поверхностная плотность материала пластинки m = 4 х + у 2. Найти массу пластинки.
- Пластинка задана ограничивающими ее кривыми: х =1/2, у = 0, у 2 =2 х (у ³ 0). Поверхностная плотность материала пластинки m = 4 х + 9 у 2. Найти ее массу.
- Интегрируема ли функция
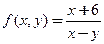 в прямоугольнике 2 £ х £ 3, 0 £ у £1?
в прямоугольнике 2 £ х £ 3, 0 £ у £1? - Найти объем тела, ограниченного поверхностями z = x 2 + y 2, x = y 2, х = 4, z = 0.
- Найти объем тела, ограниченного поверхностями 6 z = x 2 + y 2,
 .
.
- Вычислить
 , где Т – область, заданная неравенствами:
, где Т – область, заданная неравенствами: 
- Вычислить
 , где Т – область, ограниченная поверхностью x 2 + y 2 + z 2=4 z.
, где Т – область, ограниченная поверхностью x 2 + y 2 + z 2=4 z. - Вычислить
 , где T – область, ограниченная поверхностями: y = 10 x, y = 0, x = 1, z = xy, z = 0.
, где T – область, ограниченная поверхностями: y = 10 x, y = 0, x = 1, z = xy, z = 0. - Вычислить
 , где Т – область, ограниченная поверхностями
, где Т – область, ограниченная поверхностями  , z = 0.
, z = 0. - Вычислить
 , где Т – область, ограниченная поверхностями z = 3 –
, где Т – область, ограниченная поверхностями z = 3 –  , z = 0.
, z = 0. - Вычислить
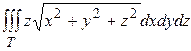 , где область Т = {(x, y, z): x 2 + y 2 + z 2 £ 1, x ³0, y ³0, z ³0}.
, где область Т = {(x, y, z): x 2 + y 2 + z 2 £ 1, x ³0, y ³0, z ³0}.