Индивидуальный индекс товарооборота

Индивидуальный индекс товарооборота характеризует изменение товарооборота по одному товару и строится как отношение товарооборота отчетного периода 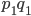к товарообороту базисного периода , то есть по формуле:

Разница между числителем и знаменателем его покажет абсолютное изменение товарооборота в рублях за счет двух фактров: изменения количества проданного товара и изменения цены этого товара, то есть

Рассчитаем индивидуальные индексы товарооборота (10):

По телевизорам: или 99% и млн.руб, то есть товарооборот по телевизорам стал меньше на 12 млн.руб, или на 1% (99-100%).

По видеомагнитофонам: 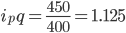или 112.5% и млн.руб, то есть товарооборот по видеомагнитофонам увеличился на 50 млн.руб. или на 12,5% (12,5-100%).

Рассмотренные нами индивидуальные индексы взаимосвязаны между собой так же, как сами индексируемые показатели: индекс товарооборота равен произведению индекса физического объема товарооборота на идекс цен, то есть

Проверим взаимосвязь исчисленных индивидуальных индексов:

§ По телевизорам: 0,99 = 0,9*1,1

§ По видеомагнитофонам: 1,125 = 1,25*0,9

Кроме того, полученные данные позволяют рассчитать абсолютные показатели изменения товарооборота по отдельным товарам за счет отдельных факторов.

Так, по телевизорам общее изменение товарооборота составило: млн.руб, то есть товарооборот по телевизорам в отчетном периоде по сравнению с базисным стал меньше на 12 млн.руб. Эта величина может быть разложена на две:

1. за счет изменения количества проданных товаров: млн.руб, то есть за счет уменьшения количества проданных телевизоров на 40 тыс.штук товарооборот стал меньше на 120 млн.руб.

2. за счет изменения цен: млн.руб, то есть за счет роста цены одного телевизора на 0,3 тыс.руб товарооборот возрос на 108 млн.руб.

Проверим взаимосвязь исчисленных показателей: млн.руб.

По видеомагнитофонам имеем изменение товарооборота на 50 млн.руб.

1. за счет изменения количества проданных товаров:

2. за счет изменения цен:

Товарооборот по видеомагнитофонам увеличился на 50 млн.руб. За счет увеличения количества проданных видеомагнитофонов на 50 тыс.штук товарооборот возрос на 100 млн.руб, а за счет снижения цен на видеомагнитофоны на 0,2 тыс.руб за штуку стал меньше на 50 млн.руб.

Билет 15.

1) Абсолютные приросты (Δy) показывают, на сколько единиц изменился последующий уровень ряда по сравнению с предыдущим (гр.3. — цепные абсолютные приросты) или по сравнению с начальным уровнем (гр.4. — базисные абсолютные приросты). Формулы расчета можно записать следующим образом:

При уменьшении абсолютных значений ряда будет соответственно "уменьшение", "снижение".

Показатели абсолютного прироста свидетельствуют о том, что, например, в 1998 г. производство продукта "А" увеличилось по сравнению с 1997 г. на 4 тыс. т, а по сравнению с 1994 г. — на 34 тыс. т.; по остальным годам см. табл. 11.5 гр. 3 и 4.

Коэффициент роста показывает, во сколько раз изменился уровень ряда по сравнению с предыдущим (гр.5 — цепные коэффициенты роста или снижения) или по сравнению с начальным уровнем (гр.6 — базисные коэффициенты роста или снижения). Формулы расчета можно записать следующим образом:

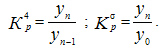
Темпы роста показывают, сколько процентов составляет последующий уровень ряда по сравнению с предыдущим (гр.7 — цепные темпы роста) или по сравнению с начальным уровнем (гр.8 — базисные темпы роста). Формулы расчета можно записать следующим образом:

Так, например, в 1997 г. объем производства продукта "А" по сравнению с 1996 г. составил 105,5 % (

Темпы прироста показывают, на сколько процентов увеличился уровень отчетного периода по сравнению с предыдущим (гр.9- цепные темпы прироста) или по сравнению с начальным уровнем (гр.10- базисные темпы прироста). Формулы расчета можно записать следующим образом:

Т_пр = Т_р - 100% или Т_пр= абсолютный прирост / уровень предшествующего периода * 100%

Так, например, в 1996 г. по сравнению с 1995 г. продукта "А" произведено больше на 3,8 % (103,8 %- 100%) или (8:210)х100%, а по сравнению с 1994 г. — на 9% (109% — 100%).

Если абсолютные уровни в ряду уменьшаются, то темп будет меньше 100% и соответственно будет темп снижения (темп прироста со знаком минус).

Абсолютное значение 1% прироста (гр. 11) показывает, сколько единиц надо произвести в данном периоде, чтобы уровень предыдущего периода возрос на 1 %. В нашем примере, в 1995 г. надо было произвести 2,0 тыс. т., а в 1998 г. — 2,3 тыс. т., т.е. значительно больше.

Определить величину абсолютного значения 1% прироста можно двумя способами:

§ уровень предшествующего периода разделить на 100;

§ цепные абсолютные приросты разделить на соответствующие цепные темпы прироста.

Абсолютное значение 1% прироста =

В динамике, особенно за длительный период, важен совместный анализ темпов прироста с содержанием каждого процента прироста или снижения.

Заметим, что рассмотренная методика анализа рядов динамики применима как для рядов динамики, уровни которых выражены абсолютными величинами (т, тыс. руб., число работников и т.д.), так и для рядов динамики, уровни которых выражены относительными показателями (% брака, % зольности угля и др.) или средними величинами (средняя урожайность в ц/га, средняя заработная плата и т.п.).

Наряду с рассмотренными аналитическими показателями, исчисляемыми за каждый год в сравнении с предшествующим или начальным уровнем, при анализе рядов динамики необходимо исчислить средние за период аналитические показатели: средний уровень ряда, средний годовой абсолютный прирост (уменьшение) и средний годовой темп роста и темп прироста.

Методы расчета среднего уровня ряда динамики были рассмотрены выше. В рассматриваемом нами интервальном ряду динамики средний уровень ряда исчисляется по формуле средней арифметической простой:

Среднегодовой объем производства продукта за 1994- 1998 гг. составил 218,4 тыс. т.

Среднегодовой абсолютный прирост исчисляется также по формуле средней арифметической простой:

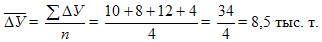
Ежегодные абсолютные приросты изменялись по годам от 4 до 12 тыс.т (см.гр.3), а среднегодовой прирост производства за период 1995 — 1998 гг. составил 8,5 тыс. т.

Методы расчета среднего темпа роста и среднего темпа прироста требуют более подробного рассмотрения. Рассмотрим их на примере приведенных в таблице годовых показателей уровня ряда.

2)

Показатели вариации делятся на две группы: абсолютные и относительные.

К абсолютным относятся размах вариации (R), среднее линейное отклонение (), дисперсия (δ²), среднее квадратическое отклонение (δ), квартильное отклонение Q.

Относительными показателями вариации являются коэффициент осцилляции, вариации, относительное линейное отклонение, относительный показатель квартильной вариации и др. Они вычисляются как отношение абсолютных показателей вариации к средней арифметической или медиане.

Самым простым абсолютным показателем является размах вариации. Его исчисляют как разность между наибольшим и наименьшим значениями варьирующего признака.

 

 

Величина R всецело зависит от крайних значений признака, и он не учитывает всех изменений варьирующего признака в пределах совокупности

Более точно характеризуют вариацию признака показатели, основанные на учете колеблемости всех значений признака, - среднее линейное отклонение (d) и среднее квадратическое отклонение (δ).

Распределение отклонений можно уловить, исчислив о тклонения всех вариант от средней. Отклонение от средней - это разность между вариантой (х) и средней арифметической () в данной совокупности.

Чтобы исчислить среднее арифметическое из отклонений нужно применить формулу средней арифметической:

а) простую ; б) взвешенную .

- среднее арифметическое или среднее линейное отклонение, дает абсолютную меру вариации.

Среднее арифметическое отклонение как мера вариации применяется редко. Чаще отклонения от средней возводят в квадрат и из квадратов исчисляют среднюю величину. Эта мера вариации называется дисперсией ( - средний квадрат отклонений), а корень квадратный из - - есть среднее квадратическое отклонение.

Чтобы вычислить среднее квадратическое отклонение нужно найти отклонение каждой варианты от средней (), затем возвести отклонения в квадрат, умножить каждый квадрат отклонения на свою частоту и просуммировать. Полученную сумму разделить на сумму частот.

=

Корень квадратный из этой величины и будет среднее квадратическое отклонение.

=

 

Помимо абсолютных величин представляют интерес и относительные величины. Для оценки интенсивности вариации, а так же для сравнения ее величины в разных совокупностях или по разным признакам используют относительные показатели вариации.Базой для сравнения является средняя арифметическая (). Они вычисляются как отношение R, (среднее линейное отклонение) и (среднее квадратическое отклонение) к или медиане. Выражаются в %; дают оценку вариации и характеризуют однородность совокупности.

Различают следующие относительные показатели вариации:

1. коэффициент осцилляции =

2. линейный коэффициент вариации =

3. коэффициент вариации =

4. коэффициент квартильной вариации

;

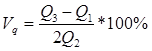
16 билет.

Разобран ранее

17 билет.

1) Разобрано

2) Метод аналитического выравнивания используется для изучения сезонных колебаний.

Сезонными называются периодические колебания, возникающие под влиянием смены времени года.

Для познания закономерностей развития социально-экономических явлений во внутригодовой динамике необходимо иметь количественные характеристики развития изучаемых явлений по месяцам и кварталам годового цикла.

Сезонные колебания присутствуют во всех сферах жизни общества: в производстве, обращении, потреблении. Большое значение сезонные колебания приобретают в изучении покупательского спроса населения на отдельные товары и виды услуг, а также на изменение цен и инфляцию. Цель изучения сезонных колебаний – это прогнозирование и разработка оперативных мер по управлению их развитием во времени.

Сезонные колебания характеризуются индексами сезонности. Для выявления сезонных колебаний обычно берут данные за ряд лет, чтобы выявить устойчивую сезонную волну. Если ряд динамики содержит определенную тенденцию в развитии явления, то сначала осуществляют аналитическое выравнивание ряда, затем сравнивают фактические теоретические уровни. Индекс сезонности в этом случае равен

где n – число лет, за которые даны уровни;

у_ф – фактические данные;

У_t – теоретические данные.

Расчет сезонных колебаний можно выполнять другим методом в зависимости от характера динамики.

Если годовой уровень явления из года в год остается относительно неизменным, то индексы сезонности исчисляются по формуле

.

Для сопоставления величины сезонных колебаний по нескольким предприятиям или периодам может быть использовано среднее квадратическое отклонение, исчисляемое по формуле

где n – число месяцев;

J_сез. – индекс для каждого месяца.

Чем меньше среднее квадратическое отклонение, тем меньше величина сезонных колебаний.

18 билет.

1)

Наименование индекса	Формула	Что показывает индекс	Что показывает значение индекса, уменьшенное на 100%	Что показывает разность числителя и знаменателя
Индекс физического объема продукции (по цене)		Во сколько раз изменилась стоимость продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения ее физического объема	На сколько процентов изменилась стоимость продукции в результате изменения объема ее производства	На сколько рублей изменилась стоимость продукции в результате роста (уменьшения) объема ее производства
Индекс цен		Во сколько раз изменилась стоимость продукции в результате изменения цен, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения цен	На сколько процентов изменилась стоимость продукции в результате изменения цен	На сколько рублей изменилась стоимость продукции в результате роста (уменьшения) цен
Индекс стоимости продукции (товарооборота)		Во сколько раз изменилась стоимость продукции, или сколько процентов составил рост (снижение) стоимости продукции в текущем периоде по сравнению с базисным	На сколько процентов изменилась стоимость продукции в текущем периоде по сравнению с базисным	На сколько рублей изменилась стоимость продукции в текущем периоде по сравнению с базисным
Индекс физического объема продукции (по себестоимости)		Во сколько раз изменились издержки производства продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) издержек производства продукции из-за изменения объема ее производства	На сколько процентов изменились издержки производства продукции в результате изменения объема ее производства	На сколько рублей изменились издержки производства продукции в результате изменения объема ее производства
Индекс себестоимости продукции		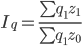Во сколько раз изменились издержки производства продукции в результате изменения себестоимости продукции, или сколько процентов составил рост (снижение) издержек производства продукции из-за изменения себестоимости продукции	На сколько процентов изменились издержки производства продукции в результате изменения себестоимости продукции	На сколько рублей изменились издержки производства продукции в результате изменения себестоимости продукции
Индекс издержек производства		Во сколько раз изменились издержки производства продукции, или сколько процентов составил рост (снижение) издержек производства продукции в текущем периоде по сравнению с базисным	На сколько процентов изменились издержки производства продукции в текущем периоде по сравнению с базисным	На сколько рублей изменились издержки производства продукции в текущем периоде по сравнению с базисным
Индекс физического объема продукции (по трудоемкости)		Во сколько раз изменились затраты времени на производство продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) затрат времени на производство продукции из-за изменения ее физического объема	На сколько процентов изменились затраты времени на производство продукции в результате изменения объема ее производства	На сколько человеко-часов изменились затраты времени на производство продукции в результате роста (уменьшения) объема ее производства
Индекс трудоемкости		Во сколько раз изменились затраты времени на производство продукции в результате изменения ее трудоемкости, или сколько процентов составил рост (снижение) затрат времени на производство продукции из-за изменения ее трудоемкости	На сколько процентов изменились затраты времени на производство продукции в результате изменения ее трудоемкости	На сколько человеко-часов изменились затраты времени на производство продукции в результате роста (уменьшения) ее трудоемкости
Индекс затрат времени на производство продукции		Во сколько раз изменились затраты времени на производство продукции, или сколько процентов составил рост (снижение) стоимости продукции в текущем периоде по сравнению с базисным	На сколько процентов изменились затраты времени на производство продукции в текущем периоде по сравнению с базисным	На сколько человеко-часов изменились затраты времени на производство продукции в текущем периоде по сравнению с базисным

 

2) Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:

где:

§ — значение моды

§ — нижняя граница модального интервала

§ — величина интервала

§ — частота модального интервала

§ — частота интервала, предшествующего модальному

§ — частота интервала, следующего за модальным

19 билет.

1) В общем случае при аналитическом выравнивании используется метод наименьших квадратов:

1. Система нормальных уравнений для линейной зависимости:

2. Система нормальных уравнений для полинома второй степени (параболы):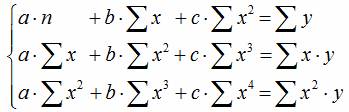

3. Система нормальных уравнений для полинома третьей степени:

2) –

 

20 билет.

1) Понятие момента широко применяется в механике для описания распределения масс (статические моменты, моменты инерции и т.д.). Совершенно теми же приемами пользуются в теории вероятностей для описания основных свойств распределения случайной величины. Чаще всего применяются на практике моменты двух видов: начальные и центральные.

Начальным моментом s-го порядка прерывной случайной величины называется сумма вида:

. (5.7.1)

Очевидно, это определение совпадает с определением начального момента порядка s в механике, если на оси абсцисс в точках сосредоточены массы .

Для непрерывной случайной величины Х начальным моментом s-го порядка называется интеграл

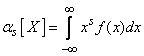. (5.7.2)

Нетрудно убедиться, что введенная в предыдущем n° основная характеристика положения – математическое ожидание – представляет собой не что иное, как первый начальный момент случайной величины .

Пользуясь знаком математического ожидания, можно объединить две формулы (5.7.1) и (5.7.2) в одну. Действительно, формулы (5.7.1) и (5.7.2) по структуре полностью аналогичны формулам (5.6.1) и (5.6.2), с той разницей, что в них вместо и стоят, соответственно, 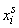и . Поэтому можно написать общее определение начального момента -го порядка, справедливое как для прерывных, так и для непрерывных величин:

, (5.7.3)

т.е. начальным моментом -го порядка случайной величины называется математическое ожидание -й степени этой случайной величины.

Перед тем, как дать определение центрального момента, введем новое понятие «центрированной случайной величины».

Пусть имеется случайная величина с математическим ожиданием . Центрированной случайной величиной, соответствующей величине , называется отклонение случайной величины от её математического ожидания:

. (5.7.4)

Условимся в дальнейшем везде обозначать центрированную случайную величину, соответствующую данной случайной величине, той же буквой со значком наверху.

Нетрудно убедиться, что математическое ожидание центрированной случайной величины равно нулю. Действительно, для прерывной величины

; (5.7.5)

аналогично и для непрерывной величины.

Центрирование случайной величины, очевидно, равносильно переносу начала координат в среднюю, «центральную» точку, абсцисса которой равна математическому ожиданию.

Моменты центрированной случайной величины носят название центральных моментов. Они аналогичны моментам относительно центра тяжести в механике.

Таким образом, центральным моментом порядка s случайной величины называется математическое ожидание -й степени соответствующей центрированной случайной величины:

, (5.7.6)

а для непрерывной – интегралом

. (5.7.8)

В дальнейшем в тех случаях, когда не возникает сомнений, к какой случайной величине относится данный момент, мы будем для краткости вместо и писать просто и .

Очевидно, для любой случайной величины центральный момент первого порядка равен нулю:

, (5.7.9)

так как математическое ожидание центрированной случайной величины всегда равно нулю.

Выведем соотношения, связывающие центральные и начальные моменты различных порядков. Вывод мы проведем только для прерывных величин; легко убедится, что точно те же соотношения справедливы и для непрерывных величин, если заменить конечные суммы интегралами, а вероятности – элементами вероятности.

Рассмотрим второй центральный момент:

Аналогично для третьего центрального момента получим:

Выражения для и т.д. могут быть получены аналогичным путем.

2)