Рассмотрим преобразование пространственных координат
где 
всегда равно 
.
Дифференцируя это выражение и учитывая, что 
получаем
откуда следует, что
и
Из формул 
видно, что выражение (1.1.2) для интервала 
преобразуется к виду
Где
Выражение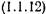 
— векторная форма метрики в стандартных координатах Шварцшильда; соответствующую скалярную форму в сферических координатах, как строгое решение уравнений Эйнштейна, впервые получил в 1916 г. К. Шварцшильд.
Мы показали, что общее выражение (1.1.2) с помощью формул (1.1.3) и (1.1.4) может быть приведено к шварцшильдовой форме (1.1.12) путем чисто алгебраического преобразования соотношения (1.1.8). Таким образом, уравнения, выведенные с использованием метрики Шварцшильда, можно преобразовать к некоторой общей сферически симметричной метрике.
Изотропные координаты
Рассмотрим систему координат, определяемую формулой
В соответствии с (1.1.3), получаем
Дифференцируя (1.1.14) по 
, находим
Следовательно, по (1.1.4) имеем
или
и выражение (1.1.2) для элемента 
принимает вид
Это выражение известно как изотропная форма метрики Шварцшильда, поскольку, приняв в 
, можно найти, что координатная
скорость света в точке х, задаваемая формулой
одинакова во всех направлениях.
УРАВНЕНИЯ ГЕОДЕЗИЧЕСКИХ
Можно показать (см. Приложение В), что уравнения, определяющие геодезические, выводятся из обычных уравнений Эйлера — Лагранжа, которые в координатах Шварцшильда имеют вид
где 
— лагранжиан,
а точка сверху обозначает дифференцирование по 
Уравнение (1.2.1) дает непосредственно
Или
где 
— постоянная интегрирования.
Формула (1.2.2) приводит к следующему выражению, вывод которого содержится в Приложении В:
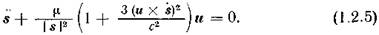
Умножая (1.2.2) векторно на 
, получаем
вследствие того что 
Таким образом,
где Н — постоянная, а h — постоянный единичный вектор. Из последнего уравнения следует, что геодезическая лежит в плоскости, перпендикулярной h, а угловой момент по отношению к собственному времени остается неизменным. Угловой момент постоянен только в координатах Шварцшильда. В произвольной метрике, для которой 
уравнение (1.2.6) имеет вид
правая часть которого не является постоянной, поскольку x — функция 
При этих условиях (1.2.6) эквивалентно уравнению
и, следовательно, уравнение геодезической (1.2.5) в координатах Шварцшильда принимает вид
Уравнение энергии
Умножение уравнения (1.2.9) скалярно на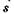 
с последующим интегрированием дает
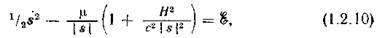
где 
— постоянная интегрирования.
Это выражение можно также получить, исключая 
из (1-2.4) и (1.2.3), с условием, что 
Это приводит к
Вследствие того что
и
левая часть (1.2.11) вдвое превышает левую часть (1.2.10) и, следователь!; о, 
Считая 
в точке, где 
из (1.2.10) находим
где
Шкалы времени
Уравнение (1.2.4)—дифференциальное, связывающее координатное и собственное время. С учетом (1.2.11) имеем
Если 
определено интегрированием формулы (1.2.9), то можно найти 
и, следовательно, получить после интегрирования выражения (1.2.15) 
как функцию 
Необходимо также выразить дифференциальное уравнение (1.2.15) через координатную скорость 
Принимая в (1.2.11)
с учетом (1.2.4) получаем
Формулы (1.2.15) и (1.2.16) можно вывести делением формулы (1.2.32) на, соответственно, 
НЬЮТОНОВО ПРИБЛИЖЕНИЕ
Принимая в уравнении (1.2.9) 
получим известное выражение для ускорения под действием закона всемирного тяготения Ньютона
Здесь мы отождествляем 
где 
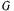— постоянная тяготения, а 
- центральная масса. В этом случае в соответствии с (1.1.13) 
а из 
Таким образом, уравнение (1.2.4) дает. 
а координатное и собственное время оказывается идентичным.
Подставив (1.3.8) в (1.2.9) и зная, что 
— произвольная функция 
можно получить уравнение геодезической в любых координатах. Очевидно, что даже и при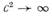 
закон обратных квадратов строго выводится только в случае постоянства к, что вновь приводит нас к стандартным координатам Шварцшильда с простой лишь сменой шкалы. Таким образом, уравнение геодезической (1.2.9) в стандартных координатах Шварцшильда является непосредственным релятивистским обобщением уравнения Ньютона (1.3.1). В этих координатах мы и будем рассматривать теорию орбитального движения, принимая ньютоново решение как первое приближение.
Теперь имеем
и, следовательно,
и далее по (3.3.1)
Учитывая, что 
—постоянный единичный вектор, интегрирование дает
где 
— произвольный постоянный единичный вектор, а е — произвольная константа. В силу перпендикулярност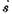и 
и 
из (1.3.3) следует, что 
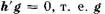перпендикулярно 
и находится в плоскости орбиты.
Умножив скалярно (1.3.3) на 
получаем
где обозначено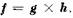 
Разделив (1.3.4) на 
, находим уравнение
орбиты
Поскольку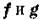 
— ортогональные единичные векторы в плоскости
орбиты, а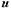 
— единичный вектор вдоль 
, можно ввести угол 
такой, что
(1.3.6)
и, следовательно, 
Отсюда можно заключить, что (1.3.5) —
уравнение конического сечения, отнесенное к фокусу как началу, с эксцентриситетом е и параметром орбиты 
Единичный вектор
направлен вдоль большой полуоси (рис. 1.1) от центра к фокусу. Можно интерпретировать полную скорость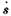 
в (1.3.3) как сумму двух векторов: один из них — постоянная скорость 
всегда перпендикулярная радиусу-вектору, а другой— постоянная скорость 
в фиксированном направлении 
вдоль малой оси сечения. Приняв большую полуось равной 
для параметра орбиты имеем 
где верхний знак относится к эллиптическому движению 
нижний — к гиперболическому 
Таким образом,
а уравнение орбиты (1.3.5) приводится к виду
Расстояние от фокуса О до ближайшей точки линии апсид 
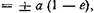поэтому полная энергия в соответствии с (1.2.13) имеет вид
поскольку в таком приближении мы полагаем, что 
или 
Уравнение (1.3.9) показывает, что при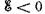 
движение стабильно
и орбита — эллипс; при 
орбита — гипербола; наконец, если
орбита — парабола. Уравнение энергии в ньютоновом приближении выводится из
(1.3.9) при 
Использованная литература:
1» Абалакин В, К Основы эфемеридной астрономии,—М.: Наука, 1979.— 448 с,
2, Бакулин Л, И., Блинов Н. С. Служба точного времени, 2-е изд. М.» Наука 1977.—352 с. Бакулин П. И. Фундаментальные каталоги звезд, 2-е изд. М.: Наука, 1980 — 336 с.
4.Блажко С. Н, Курс практической астрономии» 4-е изд.М.: Наука, 1979.— 432 с.
5.Бугославская Е. Я- Фотографическая астрометрия,— М.: Гостехиздат, 1947 — 296 с.
8. Губанов В. С, Финкельштейн А. М., Фридман П. А. Введение в радиоастрометрию.— М.: Наука, 1983.— 280 с.
7.Гуляев А. П., Хоммик Л. М. Дифференциальные каталоги звезд.— М.: Наука 1983.-136 с.
8.Загребин Д. В, Введение в астрометрию.— М.: Наука, 1966.— 280 с.