Простая линейная регрессия.

Содержание

Лабораторная работа №1. Использование регрессионного анализа в решении экономических задач. 4

1.1. Цель работы. 4

1.2. Методические рекомендации. 4

1.3. Задания. 8

Лабораторная работа №2. Использование надстройки "Поиск решения". 11

2.1. Цель работы. 11

2.2. Методические рекомендации. 11

2.3. Задание. 16

Лабораторная работа №3. Решение экономических задач с использованием финансовых функций Excel. 19

3.1. Цель работы. 19

3.2. Методические рекомендации. 19

3.3. Задание. 23

Содержание отчета: 26

 

 

Лабораторная работа №1. Использование регрессионного анализа в решении экономических задач.

Цель работы.

Научиться использовать функции, аппроксимирующие известные данные по линейной и экспоненциальной зависимости. Исследовать множественную линейную регрессию.

Методические рекомендации.

Функции регрессии.

Для решения различных экономических задач широко используются электронные таблицы Excel. Например, для обработки статистической информации в Excel предусмотрены функции регрессии, которые вычисляют параметры для линий, наилучшим образом аппроксимирующих функциональные зависимости.

Регрессия – это широко применяемый в статистике способ формирования уравнения, которое наилучшим образом описывает последовательность данных.

Попросту говоря, если мы имеем некоторую последовательность данных (см. Рис. 1), мы можем попытаться подобрать функцию, наилучшим образом описывающую полученную зависимость (см. Рис.2 и Рис.3).

 

 

Рисунок 1. Известные данные.

 

Рисунок 2. Аппроксимация по прямой.

 

 

Рисунок 3. Аппроксимация по экспоненте.

Далее мы должны оценить, какая линия описывает нашу зависимость наиболее точно, используя величину достоверности (R²) или коэффициент корреляции (функция КОРРЕЛ). В нашем примере наиболее достоверна аппроксимация по прямой. Следовательно, именно эта функция даст наиболее достоверное предсказание для будущих значений.

В следующей таблице приведены функции регрессии Excel.

Таблица 1. Описание основных функций регрессионного анализа.

Синтаксис	Описание
ЛИНЕЙН (известные_значения_y; известные_значе­ния_x; константа; статистика)	Возвращает массив, описывающий прямую, наилучшим способом аппроксимирующую имеющиеся данные (в соответствии с методом наименьших квадратов).
ТЕНДЕНЦИЯ (известные_значения_y; известные_значения_x; новые_значения_x; константа)	Возвращает значения в соответствии с линейным трендом. Аппроксимирует прямой (по методу наименьших квадратов) массивы известные_значения_y и известные_значения_x. Возвращает значения y, в соответствии с этой прямой для заданного массива новые_значения_x.
ПРЕДСКАЗ (новое_значение_x; известные_значения_y; известные_значения_x)	Вычисляет будущее значение y по существующим значениям x на основе линейной регрессии для массивов известные_ значения_ y; известные_ значения_ x.
НАКЛОН (известные_значения_y; известные_значения_x)	Возвращает наклон линии линейной регрессии, заданной точками известные_значения_y и известные_значения_x (построенной по методу наименьших квадратов).
СТОШYX (известные_значения_y; известные_значения_x)	Возвращает стандартную ошибку предска­занных значений y для каждого значения x в регрессии. Стандартная ошибка - это мера ошибки предсказанного значения y для отдельного значения x.
ЛГРФПРИБЛ (известные_значения_y; известные_значения_x; константа; статистика)	В регрессивном анализе вычисляет экспоненциальную кривую, аппроксимирующую данные и возвращает массив значений, описывающий эту кривую.
РОСТ (известные_значения_y; известные_значения_x; новые_значения_x; константа)	Аппроксимирует экспоненциальную кривую (известные_значения_y; известные_значения_x) и возвращает соответствующие этой кривой значения y, определяемые аргументом новые_значения_x. Функция РОСТ может применяться также для аппроксимации существу­ющих x- и y- значений экспоненциальной кривой
КОРРЕЛ (известные_значения_y; новые_значения_ y)	Возвращает коэффициент корреляции, показывающий насколько достоверны полученные данные. Коэффициент корреляции имеет значение от 0 до 1. Чем ближе к 1, тем достовернее результат.

Обратите внимание, что функции ЛИНЕЙН и ТЕНДЕНЦИЯ фактически возвращают одну и ту же прямую. Отличие заключается в том, что функция ЛИНЕЙН возвращает уравнение прямой y = mx + b (коэффициенты m и b), а ТЕНДЕНЦИЯ вычисляет значения y для всех известных x. Функция ПРЕДСКАЗ возвращает единственное значение y для нового x.

Функции ЛГРФПРИБЛ и РОСТ аналогичны ЛИНЕЙН и ТЕНДЕНЦИЯ, но описывают не прямую, а экспоненту (y = b× m^x).

Некоторые из этих функций (ЛИНЕЙН и ЛГРФПРИБЛ) возвращают массивы значений, поэтому они должны вводиться как формулы для работы с массивами.

Напоминаем, что формула массива может выполнить несколько вычислений, а затем вернуть одно значение или группу значений. Формула массива создается так же, как и простая формула. Выделяется ячейка или группа ячеек, в которых необходимо создать формулу, вводится формула, а затем нажимаются клавиши CTRL+SHIFT+ENTER.

Простая линейная регрессия.

Задача:

Определить доход мебельного салона в четвертом квартале на основании имеющихся данных за предыдущие месяцы.

Решение:

В случае простой линейной регрессии y = mx + b, задача может решаться несколькими способами:

1 способ. С помощью мастера функций.

Исходные данные занесем в таблицу:

 

 

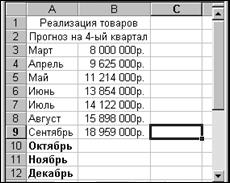Рисунок 4. Исходные данные для функции ЛИНЕЙН.

 

Решим задачу, используя простую линейную регрессию, которая описывается уравнением прямой линии y=mx+b. С помощью функции {=ЛИНЕЙН(C3:C9; A3:A9; ИСТИНА)} найдем значения коэффициентов m и b. Они равны { 1726107,14; 6191571,43 }. Теперь подставим найденные значения в уравнение прямой линии и получим интересующие нас данные.

 

 

Рисунок 5. Результат функции ЛИНЕЙН.

 

2 способ. С помощью маркера заполнения.

Выделим группу ячеек с исходными данными (диапазон В3:В9 на рис.6).

В нижней части выделенного диапазона правой кнопкой мыши захватить маркер заполнения и протащить до конца того диапазона, который требуется заполнить (диапазон В10:В12). Отпустите кнопку мыши появиться контекстное меню.

Выберите из меню пункт Линейное приближение и получите результат.

 

 

Рисунок 6. Использование маркера заполнения.

 

3 способ. С помощью команды автозаполнение.

Выделите весь диапазон, включая пустые ячейки, а затем выберите Правка — Заполнить — Прогрессия. В появившемся диалоговом окне выбрать пункт Автозаполнение.

Этим же способом можно воспользоваться, если рост происходит по экспоненциальному закону. Для этого вместо команды Линейное приближение выберите команду Экспоненциальное приближение.

 

4 способ. Графический метод.

Коэффициенты m и b можно найти и так:

1. Построить точечный график по диапазону ячеек В3:В9.

2. Выделить точки графика и вызвать контекстное меню правой кнопкой мыши.

3. В меню выбрать команду Добавить Линию тренда.

4. Задать следующие параметры: Тип - Линейная, Параметры - Прогноз - Вперед на 3 периода, Показать уравнение и величину достоверности аппроксимации.

5. Если величина достоверности аппроксимации R²@0,9-1, то данную зависимость можно использовать для предсказания результата.

6. Для расчета объема реализации продукции на 4-ый квартал используем полученное уравнение (см. рис.7)

 

 

 

Рисунок 7. Графический метод.