При работе с поиском решения следует выделить следующие этапы:
1) Построение математической модели:
a. определите целевую функцию – с какой целью выполняется расчет (минимизировать расходы, получить максимальную прибыль и т.д.);
b. определите накладываемые ограничения – возможно, некоторые значения должны лежать в определенных пределах, быть неотрицательными, целыми и т.д.;
c. определите изменяемые значения – что вы хотите найти (к-во перевозимой продукции, число сотрудников и т.д.);
d. определите сбалансированность задачи – возможно ли одновременное выполнение всех наложенных ограничений (если нет, необходимо изменить ограничения или ввести фиктивный параметр).
2) Построение расчетных таблиц:
a. занесите все известные данные на расчетный лист;
b. определитесь с изменяемыми ячейками – именно их будет заполнять Поиск решения. Это пустые ячейки без формул (иногда они содержат начальные значения для расчета). Рекомендуется выделить эти ячейки каким-либо цветом;
c. заполните ячейки с формулами – в них обязательно должны содержаться ссылки на изменяемые ячейки;
d. решите, какая ячейка будет целевой. Если необходимо найти максимум или минимум – это именно она. Если мы ищем определенное значение, целевой ячейкой может быть одна из ячейкой с формулой.
3) Вызов диалога Поиск решения:
a. Диалоговое окно Поиска решения выглядит следующим образом:
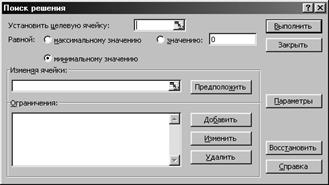 |
Рисунок 8. Окно ПОИСКА РЕШЕНИЯ.
Окно состоит из следующих элементов:
Установить целевую ячейку - служит для указания целевой ячейки, значение которой необходимо максимизировать, минимизировать или установить равным заданному числу. Эта ячейка должна содержать формулу.
Изменяя ячейки - служит для указания ячеек, значения которых изменяются в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации значения ячейки, указанной в поле Установить целевую ячейку. Изначально эти ячейки должны оставаться пустыми или содержать начальные значения для расчета.
Предположить - используется для автоматического поиска изменяемых ячеек.
Ограничения - служит для отображения списка ограничений поставленной задачи.
Добавить - служит для отображения диалогового окна Добавить ограничение (Рисунок 9).

Рисунок 9. Добавление ограничений.
Ограничения позволяют заранее указать, какими должны быть значения в отдельных ячейках: неотрицательными, целыми, больше или меньше определенного числа и т.д.
Изменить - служит для отображения диалоговое окна «Изменить ограничение».
Удалить - служит для снятия указанного ограничения.
Выполнить - служит для запуска поиска решения поставленной задачи.
Закрыть - служит для выхода из окна диалога без запуска поиска решения поставленной задачи.
Параметры - служит для отображения диалогового окна «Параметры поиска решения», в котором можно загрузить или сохранить оптимизируемую модель и указать предусмотренные варианты поиска решения.
Восстановить - служит для очистки полей окна диалога и восстановления значений параметров поиска решения, используемых по умолчанию.
Пример.
Имеются n пунктов производства (фабрик) и m пунктов распределения продукции (складов). Стоимость перевозки единицы продукции с i -ой фабрики на j -й склад cij приведена в таблице, где под строкой понимается фабрика, а под столбцом – склад. Кроме того, в этой таблице, в i -й строке указан объем производства на i -ой фабрике, а j -м столбце указан объем производства на j -ой фабрике (см. Таблицу 7). Необходимо составить план перевозок по доставке требуемой продукции на склады, с минимальными суммарными транспортными расходами.
В данном случае задача не сбалансирована, т.е. объем производства (20+30+30+20+17=117) не равен объему потребляемой продукции (50+30+20+20=120). Для сбалансирования задачи введем дополнительно фиктивную фабрику и примем стоимость перевозки равной стоимости штрафа за недопоставку продукции (к примеру – 10), а объем перевозок – объемам недопоставок продукции на склады (в данном случае - 3).
Таблица 7.
| Стоимость перевозки единицы продукции | ||||||
| Потребление | ||||||
| Склад 1 | Склад 2 | Склад 3 | Склад 4 | Объемы производства | ||
| Производство | Фабрика 1 | |||||
| Фабрика 2 | ||||||
| Фабрика 3 | ||||||
| Фабрика 4 | ||||||
| Фабрика 5 | ||||||
| Фиктивная фабрика | ||||||
| Объемы потребления |
Составим математическую модель:
Пусть xij –объём перевозок с i -й фабрики на j -й склад.
Суммарная стоимость всех перевозок  cij• xij, где cij - стоимость перевозки единицы продукции с i -й фабрики ны j -й склад.
cij• xij, где cij - стоимость перевозки единицы продукции с i -й фабрики ны j -й склад.
Неизвестные должны удовлетворять следующим ограничениям:
1. Объемы перевозок не могут быть отрицательными.
2. Так как модель сбалансирована, то вся продукция должна быть вывезена с фабрики, а потребности всех складов должны быть удовлетворены.
Модель:
Минимизировать:
 cij xij
cij xij
при ограничениях:  ,
, 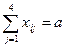 ,
,  ,
,  ,
, 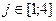
где ai - объем производства на i - й фабрике, bj спрос на j -м складе.
Решение.
Решим данную задачу с помощью Поиска решения.
Построим еще одну таблицу, которая будет заполнена объемами перевозок.
Таблица 8. Таблица с исходными ячейками для ПОИСКА РЕШЕНИЯ.
| Объемы перевозки продукции | |||||||
| Потребление | |||||||
| Склад 1 | Склад 2 | Склад 3 | Склад 4 | Суммарное производство | Объемы производства | ||
| Производство | Фабрика 1 | ||||||
| Фабрика 2 | |||||||
| Фабрика 3 | |||||||
| Фабрика 4 | |||||||
| Фабрика 5 | |||||||
| Фиктивная фабрика | |||||||
| Суммарное потребление | |||||||
| Объемы потребления |
Ниже вы увидите как выглядит решение этой задачи в Excel:

Рисунок 10. Данные по стоимости перевозки.
Под неизвестные отведём ячейки C14:F19, в ячейки A1:D6 введём стоимость перевозок, G14:G19 –объемы производства на фабриках, C20:F20 – потребность в продукции на складах. В ячейку G20 введём целевую функцию - =СУММПРОИЗВ(C4:F9;C14:F19).
Рисунок 11. Исходные ячейки и формулы, подготовленные для ПОИСКА РЕШЕНИЯ.

Вызовем команду поиск решения и заполним открывшееся диалоговое окно (см. рис.12).

Рисунок 12. Окно ПОИСКА РЕШЕНИЯ.
В параметрах поиска решения нужно установить флажок «линейная модель».
Результат поиска решения (см.рис.13):
Рисунок 13. Результат ПОИСКА РЕШЕНИЯ.

Анализируя полученный результат, можно видеть, что, скажем, на Склад 1 поступит 30 единиц продукции с Фабрики 2 и 20 единиц с Фабрики 4. Поскольку потребности складов превосходят мощности фабрик на 3 единицы, именно это количество продукции должно поступить на Склад 2 с фиктивной фабрики. При таком графике продукция со всех фабрик будет полностью вывезена, а потребности всех складов будут полностью удовлетворены (кроме, разумеется, Склада 2). Стоимость всех перевозок будет минимальной – 274.
Задание.
- Выполните Пример из методических материалов.
2. Планирование производства товаров.
Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуется 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного приемника первой и второй моделей равен 30 и 20 денежных. ед., соответственно. Определить оптимальный суточный объем производства первой и второй моделей.
Таблица 9. Производство радиоприемников
| К-во в день | Расход деталей на 1 приемник | Общий расход деталей | Прибыль от реализации 1 приемника | Общая прибыль | Объем произ- водства | |
| I-ая модель | ||||||
| II-ая модель | ||||||
| Итого | Итого | |||||
| Запас деталей |
3. Планирование рекламной компании.
Фирма имеет возможность рекламировать свою продукцию, используя местную радио и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены суммой 10 000 ден.ед в месяц. Каждая минута радиорекламы обходится в 5 ден.ед, а каждая минута телерекламы – в 100 ден.ед. Фирма хотела использовать радиосеть, по крайней мере, в два раза чаще, чем телевидение. Опыт прошлых лет показал, что, объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше объема сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Таблица 10. Рекламная компания.
| Объем рекламы в месяц | Стоимость 1 минуты | Стоимость за месяц | Коэффициент эффективности | Суммарная эффективность | |
| Радиореклама | |||||
| Телереклама | |||||
| Ограничение | 10 000 |
4. Планирование штатного расписания.
Авиакомпании требуется определить, сколько стюардесс следует принять на работу в течении шести месяцев при условии, что любая из них должна пройти предварительную подготовку. Потребности в количестве человеко-часов летного времени для стюардесс известны: в январе - 8 000, в феврале - 9 000, в марте 8 000, в апреле - 10 000, в мае - 9 000 и в июне - 12 000.
Подготовка стюардессы к выполнению своих обязанностей занимает один месяц. Следовательно, прием на работу должен на один месяц опережать ввод стюардессы в строй. Кроме того, каждая стюардесса должна в течении месяца, отведенного на ее подготовку, пройти 100-часовую практику непосредственно во время полетов. Таким образом, за счет каждой обучаемой стюардессы в течении месяца освобождается 100 человеко-часов летного времени, отведенного для уже обученных стюардесс.
Каждая полностью бученная стюардесса в течении месяца может иметь налет до 150 часов. Авиакомпания в начале января уже имеет 60 опытных стюардесс. При этом ни одну из них не снимают с работы. Установлено также, что приблизительно 10% обучаемых стюардесс по окончании обучения увольняются по каким -либо обстоятельствам. Опытная стюардесса обходится авиакомпании в 800 $, а обучаемая - в 400 $ в месяц. Необходимо спланировать штат авиакомпании таким образом, чтобы минимизировать издержки за отчетные шесть месяцев.
Занесите в Таблицу 11 известные данные.
Таблица 11. Штатное расписание стюардесс.
| Месяц | Число постоянно работающих стюардесс | Число новых стюардесс | Требуемое кол-во (чел./ч) | Фактическое кол-во (чел./ч) | Затраты |
| Январь | |||||
| Февраль | |||||
| Март | |||||
| Апрель | |||||
| Май | |||||
| Июнь | |||||
| Итого |
Таблица 12. Затраты и разрешенный налет на 1 стюардессу.
| Затраты на одну стюардессу, $ | Разрешенный налет, чел./ч | ||
| Обучение | Работа | Обучение | Работа |
5. Задача о назначениях. Имеется n рабочих и m видов работ. Стоимость cij выполнения i -м рабочим j –ой работы приведена в Таблице 13, где рабочему соответствует строка, а работе столбец. Необходимо составить план работ так, чтобы все работы были выполнены, каждый рабочий был занят только на одной работе, а суммарная стоимость выполнения всех работ была бы минимальной.
Таблица 13. Расценки работ.
| Вальцовка | Шлифовка | Обрезка | Укладка | Наладка | |
| Алексеев | |||||
| Петров | |||||
| Сидоренко | |||||
| Гнатюк |
Таблица 14. Выполнение работ.
| Вальцовка | Шлифовка | Обрезка | Укладка | Наладка | S работ, выполненных рабочим | |
| Алексеев | ||||||
| Петров | ||||||
| Сидоренко | ||||||
| Гнатюк | ||||||
| S рабочих, выполнивших работу |
