Задание 4. Выравнивание статистического распределения случайной величины

Задание 1. Определение показателей надёжности невосстанавливаемых элементов

 

Таблица 1.1

Данные об отказах

∆𝑡𝑖, ч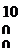

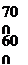
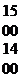
𝑛 (∆𝑡𝑖)

∆𝑡𝑖, ч

𝑛 (∆𝑡𝑖)

 

Данные о количестве элементов в эксплуатации в начальный момент: 𝑁(0) = 1090

Вероятность безотказной работы на основании статистических данных:

𝑵(𝟎) − 𝒏 (∆𝒕_𝒊)

𝑷(∆𝒕_𝒊) =

𝑵(𝟎)

𝑁(0) - количество элементов в эксплуатации в момент времени t = 0;

𝑛 (∆𝑡_𝑖) - количество отказавших элементов на интервале времени ∆𝑡_𝑖

Вероятность отказа определяется по формуле:

𝑸(∆𝒕_𝒊) = 𝟏 − 𝑷(∆𝒕_𝒊)

Интенсивность отказов:

𝒏 (∆𝒕^𝒊)

𝝀(𝒕_𝒊) =

𝑵(𝒕_𝒊) ∙ ∆𝒕_𝒊

𝑁(𝑡_𝑖) – число элементов, исправных к началу интервала ∆𝑡_𝑖;

𝑛 (∆𝑡_𝑖) - количество отказавших элементов на интервале времени ∆𝑡_𝑖;

𝑡_𝑖 – продолжительность интервала наблюдений

 

Расчётные значения 𝑃(∆𝑡_𝑖), 𝑄(∆𝑡_𝑖), 𝜆(𝑡_𝑖) занесены в таблицу 1.2

Таблица 1.2

	P(∆t)	Q(∆t)	λ(t)
	0,95	0,05	0,000486
	0,91	0,09	0,000415
	0,88	0,12	0,000352
	0,85	0,15	0,000292
	0,83	0,17	0,000247
	0,81	0,19	0,00022
	0,80	0,20	0,000214
	0,78	0,22	0,000219
	0,76	0,24	0,000212
	0,75	0,25	0,000204
	0,73	0,27	0,000221
	0,72	0,28	0,000213
	0,70	0,30	0,000218
	0,69	0,31	0,00021
	0,67	0,33	0,000228
	0,66	0,34	0,000219
	0,64	0,36	0,000224
	0,63	0,37	0,000229
	0,61	0,39	0,000249
	0,60	0,40	0,000226
	0,58	0,42	0,000231
	0,57	0,43	0,000252
	0,55	0,45	0,000242
	0,54	0,46	0,000265
	0,52	0,48	0,000289
	0,51	0,49	0,000333
	0,49	0,51	0,000417
	0,46	0,54	0,000529
	0,43	0,57	0,000659
	0,39	0,61	0,000919

 

Пример расчёта для первого интервала:

𝑃(∆𝑡₁) = = 0,95

𝑄(∆𝑡₁) = 1 − 0,95 = 0,05

𝜆

 

Средний срок службы элемента до отказа:

𝒎

ТСР = ∑ 𝒕𝒊 ∙ 𝒑𝒊

𝒊=𝟏

𝑡_𝑖 - середина i-го интервала;

m – число интервалов;

𝑝_𝑖 - статистическая вероятность события

𝒏 (∆𝒕_𝒊)

𝒑_𝒊 =

𝑵(𝟎)

Для первого интервала:

𝑝₁ = = 0,0486

𝑡₁ = 50 (ч)

𝑡₁ ∙ 𝑝₁ = 0,0486 ∙ 50 = 2,43

Средний срок службы для всех интервалов:

Т_СР 𝑡_𝑖 ∙ 𝑝_𝑖 = 860,87 (ч)

Рис. 1.1

Рис. 1.2

 

Задание 2. Определение надёжности полупроводниковых преобразователей

Исходные данные:

Тип п/п преобразователя – инвертор

Таблица 2.1

Наименование	Количество 𝑁𝑖, шт	𝜆, ч
Тиристор		1,9 ∙ 10−5
Диод		4 ∙ 10−5
Конденсаторы		0,4 ∙ 10−5
Трансформаторы дроссели		0,4 ∙ 10−5
Соединения		0,05 ∙ 10−6

 

Если отказ системы наступает при отказе одного элемента, то считается, что такая система имеет основное соединение элементов. Рассматриваемый ниже метод расчёта надёжности используется на этапе эскизного проектирования после разработки принципиальных электрических схем системы. Он позволяет оценить надёжность системы при принятой элементной базе и наметить пути повышения надёжности.

Допущения:

• все элементы данного типа равнонадёжны, т.е. величины интенсивности отказов 𝜆_𝑖 для этих элементов одинаковы;

• все элементы работают в номинальном режиме, предусмотренном ТУ;

• интенсивность отказов элементов не зависит от времени; • отказы элементов системы являются событиями и независимыми; • все элементы системы работают одновременно.

Интенсивность отказов системы:

𝒓

𝝀_С = ∑ 𝑵_𝒊 ∙ 𝝀_𝒊

𝒊=𝟏

𝑁_𝑖 – число элементов i-го типа; r – число типов элементов;

𝜆_𝑖 - интенсивность отказа i-го элемента.

Тиристоры:

𝜆

час

 

 

Диоды:

𝜆

час Конденсаторы:

𝜆

час

Трансформаторы, дроссели:

𝜆

час Соединения:

𝜆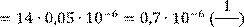

час

 

𝜆_С

час Средний срок службы системы до первого отказа:

𝟏

ТСР.С =

𝝀_С

Т_СР.

Вероятность безотказной работы элементов системы за время t:

Р_С 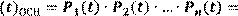𝒆 𝝀^𝑪𝒕

𝑃 - вероятность безотказной работы элемента системы

Таблица 2.2

𝑡, час
𝑃(𝑡)		0,87	0,77	0,67	0,59	0,52	0,45	0,4	0,35	0,3	0,27

 

РС(𝒕)ОСН = 𝒆−𝝀𝑪𝒕

Р_С

Р_С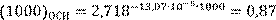

Рис. 2.1

 

Задание 3. Расчёт надёжности систем на резервном соединении элементов

Исходные данные:

𝑃_𝑖(𝑡) = 0,98 m = 8

n = 6

Расчётная схема системы:

Рис. 3.1

 

Определение надёжности системы:

𝑷𝑪(𝒕) = 𝟏 − [𝟏 − П𝒏𝒊=𝟏𝑷𝒊(𝒕)]𝒎+𝟏

Так как:

𝑃₁(𝑡) = 𝑃₂(𝑡) = 𝑃₃(𝑡) = 𝑃₄(𝑡) = 𝑃₅(𝑡) = 𝑃₆(𝑡) = 0,98, То:

𝑷_𝑪(𝒕) = 𝟏 − [𝟏 − 𝑷_𝒊(𝒕)^𝒏]^𝒎+𝟏

𝑃_𝐶(𝑡) = 1 − [1 − 0,98⁶]⁹ = 0,99

Задание 4. Выравнивание статистического распределения случайной величины

 

Исходные данные

Таблица 4.1

∆𝑡𝑖, ч

𝑛 (∆𝑡𝑖)

 

Количество систем – 75

Считать, что для рассматриваемых систем управления справедлив экспоненциальный закон надёжности:

T

𝑷(𝒕) = 𝒆−1

где Т = 17,1 ч.

Таблица 4.2

Интервалы времени ∆𝑡𝑖, ч	Отказы с момента начала эксплуатации
Количество отказавших систем 𝑛 (∆𝑡𝑖)	Статистическая вероятность события 𝑛 (∆𝑡 𝑃̅ = 𝑖) 𝑁
0-5		0,04
5-10		0,09
10-15		0,12
15-20		0,05
20-25		0,09
25-30		0,11
30-35		0,08
35-40		0,07
40-45		0,03
45-50		0,04
50-55		0,03
55-60		0,03
60-65		0,07
65-70		0,06
70-75		0,06
75-80		0,03

 

 

Пример расчёта для ∆𝑡₁:

𝑃̅(1) = = 0,04

Таблица 4.3

𝑇, ч	𝑄̅(𝑡)	𝑃̅(𝑡)	𝑃(𝑡)
	0,04	0,96	0,74
	0,13	0,87	0,55
	0,25	0,75	0,42
	0,3	0,7	0,31
	0,39	0,61	0,23
	0,5	0,5	0,17
	0,58	0,42	0,13
	0,65	0,35	0,09
	0,68	0,32	0,07
	0,72	0,28	0,05
	0,75	0,25	0,04
	0,78	0,22	0,03
	0,85	0,15	0,02
	0,91	0,09	0,016
	0,97	0,03	0,012
			0,009

 

Пример расчёта для Т=0

𝑃̅(0) = 1 − 𝑄̅(0) = 1 − 0 = 1

0

𝑃(0) = 2,718^−17,1 = 1

Под выравниванием статистического распределения подразумевается обработка статистических данных, при которой обеспечивается подбор наиболее подходящего теоретического закона распределения.

Для оценки степени расхождения полученного статистического распределения 𝑃̅(𝑡) с теоретическим 𝑃(𝑡) выбирается мера расхождения:

𝑫 𝝀

по величине которой можно судить о том, вызвано ли расхождение случайными причинами или разница между распределениями настолько велика, что выбранный теоретический закон 𝑃(𝑡) непригоден.

 

Рис. 4.1

Согласно рис. 4.1, D = 0,39, значит:

𝜆

Вывод: так как 𝜆 = 3,37, значит 𝑝(𝜆) < 0,05 и, следовательно, выбранный теоретический закон распределения непригоден для решения данной задачи.