Содержание
Введение..................................................................................................
1. Классификация СМО и их основные элементы...............................
2. Обслуживание с ожиданием..............................................................
3. Пример использования СМО с ожиданием......................................
Расчеты...................................................................................................
Выводы...................................................................................................
Список литературы................................................................................
Приложение 1.........................................................................................
Приложение 2.........................................................................................
ВВЕДЕНИЕ
Во многих областях практической деятельности человека мы сталкиваемся с необходимостью пребывания в состоянии ожидания. Подобные ситуации возникают в очередях в билетных кассах, в крупных аэропортах, при ожидании обслуживающим персоналом самолетов разрешения на взлет или посадку, на телефонных станциях в ожидании освобождения линии абонента, в ремонтных цехах в ожидании ремонта станков и оборудования, на складах снабженческо-сбытовых организаций в ожидании разгрузки или погрузки транспортных средств. Во всех перечисленных случаях имеем дело с массовостью и обслуживанием. Изучением таких ситуаций занимается теория массового обслуживания.
В теории систем массового обслуживания (в дальнейшем просто -CMÎ) обслуживаемый объект называют требованием. В общем случае под требованием обычно понимают запрос на удовлетворение некоторой потребности, например, разговор с абонентом, посадка самолета, покупка билета, получение материалов на складе.
Средства, обслуживающие требования, называются обслуживающими устройствами или каналами обслуживания. Например, к ним относятся каналы телефонной связи, посадочные полосы, мастера-ремонтники, билетные кассиры, погрузочно-разгрузочные точки на базах и складах.
Совокупность однотипных обслуживающих устройств называется îáñëóæèâàþùèìè óñòðîéñòвами. Такими системами могут быть телефонные станции, аэродромы, билетные кассы, ремонтные мастерские, склады и базы снабженческо-сбытовых организаций и т.д.
В теории СМО рассматриваются такие случаи, когда поступление требований происходит через случайные промежутки времени, а продолжительность обслуживания требований не является постоянной, т.е. носит случайный характер. В силу этих причин одним из основных методов математического описания СМО является аппарат теории случайных процессов.
Основной задачей теории СМО является изучение режима функционирования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания. Так, одной из характеристик обслуживающей системы является время пребывания требования в очереди. Очевидно, что это время можно сократить за счет увеличения количества обслуживающих устройств. Однако каждое дополнительное устройство требует определенных материальных затрат, при этом увеличивается время бездействия обслуживающего устройства из-за отсутствия требований на обслуживание, что также является негативным явлением. Следовательно, в теории СМО возникают задачи оптимизации: каким образом достичь определенного уровня обслуживания (максимального сокращения очереди или потерь требований) при минимальных затратах, связанных с простоем обслуживающих устройств.
Раздел І. Классификация СМО и их
Основные элементы
СМО классифицируются на разные группы в зависимости от состава и от времени пребывания в очереди до начала обслуживания, и от дисциплины обслуживания требований.
По составу СМО бывают одноканальные (с одним обслуживающим устройством) и многоканальными (с большим числом обслуживающих устройств). Многоканальные системы могут состоять из обслуживающих устройств как одинаковой, так и разной производительности.
По времени пребывания требований в очереди до начала обслуживания системы делятся на три группы:
1) с неограниченным временем ожидания (с ожиданием ),
2) с отказами;
3) смешанного типа.
В СМО с неограниченным временем ожидания очередное требование, застав все устройства занятыми, становится в очередь и ожидает обслуживания до тех пор, пока одно из устройств не освободится.
В системах с отказами поступившее требование, застав все устройства занятыми, покидает систему. Классическим примером системы с отказами может служить работа автоматической телефонной станции.
В системах смешанного типа поступившее требование, застав все (устройства занятыми, становятся в очередь и ожидают обслуживания в течение ограниченного времени. Не дождавшись обслуживания в установленное время, требование покидает систему.
В системах с определенной дисциплиной обслуживания поступившее требование, застав все устройства занятыми, в зависимости от своего приоритета, либо обслуживается вне очереди, либо становится в очередь.
Основными элементами СМО являются: входящий поток требований, очередь требований, обслуживающие устройства, (каналы) и выходящий поток требований.
Изучение СМО начинается с анализа входящего потока требований. Входящий поток требований представляет собой совокупность требований, которые поступают в систему и нуждаются в обслуживании. Входящий поток требований изучается с целью установления закономерностей этого потока и дальнейшего улучшения качества обслуживания.
В большинстве случаев входящий поток неуправляем и зависит от ряда случайных факторов. Число требований, поступающих в единицу времени, случайная величина. Случайной величиной является также интервал времени между соседними поступающими требованиями. Однако среднее количество требований, поступивших в единицу времени, и средний интервал времени между соседними поступающими требованиями предполагаются заданными.
Среднее число требований, поступающих в систему обслуживания за единицу времени, называется интенсивностью поступления требований и определяется следующим соотношением:
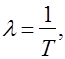
где Т - среднее значение интервала между поступлением очередных требований.
Для многих реальных процессов поток требований достаточно хорошо описывается законом распределения Пуассона. Такой поток называется простейшим.
Простейший поток обладает такими важными свойствами:
1) Свойством стационарности, которое выражает неизменность вероятностного режима потока по времени. Это значит, что число требований, поступающих в систему в равные промежутки времени, в среднем должно быть постоянным. Например, число вагонов, поступающих под погрузку в среднем в сутки должно быть одинаковым для различных периодов времени, к примеру, в начале и в конце декады.
2) Отсутствия последействия, которое обуславливает взаимную независимость поступления того или иного числа требований на обслуживание в непересекающиеся промежутки времени. Это значит, что число требований, поступающих в данный отрезок времени, не зависит от числа требований, обслуженных в предыдущем промежутке времени. Например, число автомобилей, прибывших за материалами в десятый день месяца, не зависит от числа автомобилей, обслуженных в четвертый или любой другой предыдущий день данного месяца.
3) Свойством ординарности, которое выражает практическую невозможность одновременного поступления двух или более требований (вероятность такого события неизмеримо мала по отношению к рассматриваемому промежутку времени, когда последний устремляют к нулю).
При простейшем потоке требований распределение требований, поступающих в систему подчиняются закону распределения Пуассона:
вероятность 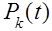 того, что в обслуживающую систему за время t поступит именно k требований:
того, что в обслуживающую систему за время t поступит именно k требований:

где 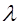 . - среднее число требований, поступивших на обслуживание в единицу времени.
. - среднее число требований, поступивших на обслуживание в единицу времени.
На практике условия простейшего потока не всегда строго выполняются. Часто имеет место нестационарность процесса (в различные часы дня и различные дни месяца поток требований может меняться, он может быть интенсивнее утром или в последние дни месяца). Существует также наличие последействия, когда количество требований на отпуск товаров в конце месяца зависит от их удовлетворения в начале месяца. Наблюдается и явление неоднородности, когда несколько клиентов одновременно пребывают на склад за материалами. Однако в целом пуассоновский закон распределения с достаточно высоким приближением отражает многие процессы массового обслуживания. Почему такое предположение в ряде важных случаев оказывается верным, дает ответ общая теорема А.Я.Хинчина, которая представляет исключительную теоретическую и практическую ценность. Эта теорема имеет место в случае, когда входящий поток можно представить в виде суммы большого числа независимых потоков, ни один из которых не является сравнимым по интенсивности со всем суммарным потоком. Приведем “не строгую” формулировку этой теоремы (полная формулировка и доказательство приведены в).
Теорема (А.Я.Хинчин) Если входящий поток представляет собой сумму большого числа независимых между собой стационарных и ординарных потоков, каждый из которых вносит малый вклад в общую сумму, то при одном дополнительном условии аналитического характера (которое обычно выполняется на практике) поток близок к простейшему.
Применение этой теоремы на практике можно продемонстрировать, на следующем примере: поток судов дальнего плавания в данный грузовой порт, связанный со многими портами мира, можно считать близким к простейшему. Это дает нам право считать поток прибытия судов в порт распределенным согласно процесса Пуассона.
Кроме тогî, наличие пуассоновского потока требований можно определить статистической обработкой данных о поступлении требований на обслуживание. Одним из признаков закона распределения Пуассона является равенство математического ожидания случайной величины и дисперсии этой же величины, т.е.
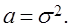
Одной из важнейших характеристик обслуживающих устройств, которая определяет пропускную способность всей системы, является в ремя обслуживания.
Время обслуживания одного требования (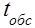 )- случайная величина, которая может изменятся в большом диапазоне. Она зависит от стабильности работы самих обслуживающих устройств, так и от различных параметров, поступающих в систему, требований (к примеру, различной грузоподъемности транспортных средств, поступающих под погрузку или выгрузку).
)- случайная величина, которая может изменятся в большом диапазоне. Она зависит от стабильности работы самих обслуживающих устройств, так и от различных параметров, поступающих в систему, требований (к примеру, различной грузоподъемности транспортных средств, поступающих под погрузку или выгрузку).
Случайная величина 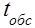 полностью характеризуется законом распределения, который определяется на основе статистических испытаний.
полностью характеризуется законом распределения, который определяется на основе статистических испытаний.
На практике чаще всего принимают гипотезу о показательном законе распределения времени обслуживания.
Показательный закон распределения времени обслуживания имеет место тогда, когда плотность распределения резко убывает с возрастанием времени t. Например, когда основная масса требований обслуживается быстро, а продолжительное обслуживание встречается редко. Наличие показательного закона распределения времени обслуживания устанавливается на основе статистических наблюдений.
При показательном законе распределения времени обслуживания вероятность  события, что время обслуживания продлиться не более чем t, равна:
события, что время обслуживания продлиться не более чем t, равна:

где v - интенсивность обслуживания одного требования одним обслуживающим устройством, которая определяется из соотношения:
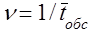 , (1)
, (1)
где 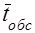
 - среднее время обслуживания одного требования одним обслуживающим устройством.
- среднее время обслуживания одного требования одним обслуживающим устройством.
Следует заметить, что если закон распределения времени обслуживания показательный, то при наличии нескольких обслуживающих устройств одинаковой мощности закон распределения времени обслуживания несколькими устройствами будет также показательным:

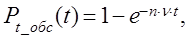
где n - количество обслуживающих устройств.
Важным параметром СМО является коэффициент загрузки  , который определяется как отношение интенсивности поступления требований
, который определяется как отношение интенсивности поступления требований 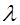 к интенсивности обслуживания v.
к интенсивности обслуживания v.
 (2)
(2)
где a - коэффициент загрузки;  - интенсивность поступления требований в систему; v - интенсивность обслуживания одного требования одним обслуживающим устройством.
- интенсивность поступления требований в систему; v - интенсивность обслуживания одного требования одним обслуживающим устройством.
Из (1) и (2) получаем, что
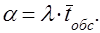
Учитывая, что  - интенсивность поступления требований в систему
- интенсивность поступления требований в систему
в единицу времени, произведение 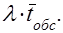 показывает количество требований, поступающих в систему обслуживания за среднее время обслуживания одного требования одним устройством.
показывает количество требований, поступающих в систему обслуживания за среднее время обслуживания одного требования одним устройством.
Для СМО с ожиданием количество обслуживаемых устройств п должно быть строго больше коэффициента загрузки (требование установившегося или стационарного режима работы СМО):
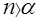 .
.
В противном случае число поступающих требований будет больше суммарной производительности всех обслуживающих устройств, и очередь будет неограниченно расти.
Для СМО с отказами и смешанного типа это условие может быть ослаблено, для эффективной работы этих типов СМО достаточно потребовать, чтобы минимальное количество обслуживаемых устройств n было не меньше коэффициента загрузки 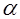 :
: 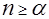
Раздел ІІ.Обслуживание с ожиданием
Постановка задачи.
СМО с ожиданием распространены наиболее широко. Их можно разбить на 2 большие группы - разомкнутые и замкнутые. Эти системы определяют так же, как системы с ограниченным входящим потоком.
К замкнутым относятся системы, в которых поступающий поток требований ограничен. Например, мастер, задачей которого является наладка станков в цехе, должен периодически их обслуживать. Каждый налаженный станок становится в будущем потенциальным источником требований на подналадку.
В подобных системах общее число циркулирующих требований конечно и чаще всего постоянно.
Если питающий источник обладает бесконечным числом требований, то системы называются разомкнутыми. Примерами подобных систем могут служить магазины, кассы вокзалов, портов и др. Для этих систем поступающий поток требований можно считать неограниченным.
Мы рассмотрим здесь классическую задачу теории массового обслуживания в тех условиях, в каких она была рассмотрена и решена К.Эрлангом. на n одинаковых приборов поступает простейший поток требований интенсивности 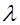 . Если в момент поступления имеется хотя бы один свободный прибор, оно немедленно начинает обслуживаться. Если же все приборы заняты, то вновь прибывшее требование становится в очередь за всеми теми требованиями, которые поступили раньше и ещё не начали обслуживаться. Освободившийся прибор немедленно приступает к обслуживанию очередного требования, если только имеется очередь. Каждое требование обслуживается только одним прибором, и каждый прибор обслуживает в каждый момент времени не более одного требования. Длительность обслуживания представляет собой случайную величину с одним и тем же распределением вероятностей F(x). Предполагается, что при x
. Если в момент поступления имеется хотя бы один свободный прибор, оно немедленно начинает обслуживаться. Если же все приборы заняты, то вновь прибывшее требование становится в очередь за всеми теми требованиями, которые поступили раньше и ещё не начали обслуживаться. Освободившийся прибор немедленно приступает к обслуживанию очередного требования, если только имеется очередь. Каждое требование обслуживается только одним прибором, и каждый прибор обслуживает в каждый момент времени не более одного требования. Длительность обслуживания представляет собой случайную величину с одним и тем же распределением вероятностей F(x). Предполагается, что при x  0.
0.

где 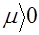 - постоянная.
- постоянная.
Только что описанная задача представляет значительный прикладной интерес, и результаты, с которыми мы познакомимся, широко используются для практических целей. Реальных ситуаций, в которых возникают подобные вопросы, исключительно много. Эрланг решил эту задачу, имея в виду постановки вопросов, возникших к тому времени в телефонном деле.
Выбор распределения (1) для описания длительности обслуживания произведен не случайно. Дело в том, что в этом предположении задача допускает простое решение, которое с удовлетворительной для практики точностью описывает ход интересующего нас процесса. Распределение (1) играет в теории массового обслуживания исключительную роль, которая в значительной мере вызвана следующим его свойством:
При показательном распределении длительности обслуживания распределение длительности оставшейся части работы по обслуживанию не зависит от того, сколько оно уже продолжалось.
Действительно, пусть 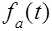 означает вероятность того, что обслуживание, которое ужо продолжается время а, продлится еще не менее чем
означает вероятность того, что обслуживание, которое ужо продолжается время а, продлится еще не менее чем 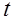 . В предположении, что длительность обслуживания распределена показательно,
. В предположении, что длительность обслуживания распределена показательно, 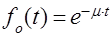 . Далее ясно, что
. Далее ясно, что 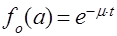 и
и 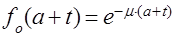 . А так как всегда и
. А так как всегда и 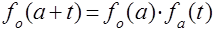 ,
, 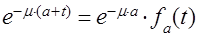 и, следовательно,
и, следовательно,
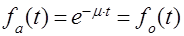
Требуемое доказано.
Несомненно, что в реальной обстановке показательное время обслуживания является, как правило, лишь грубым приближением к действительности. Так, нередко время обслуживания не может быть меньше, чем некоторая определенная величина. Предположение же (1) приводит к тому, что значительная доля требовании нуждается лишь в кратковременной операции, близкой к 0. Позднее перед нами возникает задача освобождения от излишнего ограничения, накладываемого предположением (1). Необходимость этого была ясна уже самому Эрлангу, и он в ряде работ делал усилия найти иные удачные распределения для длительности обслуживания. В частности, им было предложено так называемое распределение Эрланга, плотность распределения которого дается формулой
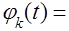

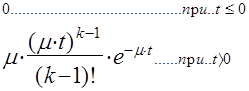
где 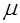 > 0, a k — целое положительное число.
> 0, a k — целое положительное число.
Распределение Эрланга представляет собой распределение суммы k- независимых слагаемых, каждое из которых имеет распределение (1).
Обозначим для случая распределения (1) через 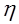 время обслуживания требования. Тогда средняя длительность обслуживания равна
время обслуживания требования. Тогда средняя длительность обслуживания равна

Это равенство даст нам cпосоá оценки параметра 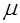 по опытным данным. Как легко вычислить, дисперсия длительности обслуживания равна
по опытным данным. Как легко вычислить, дисперсия длительности обслуживания равна