Выполнение арифметических действий в разных системах счисления.

Практическая работа №5

Тема: Перевод чисел и арифметические действия в позиционных системах счисления.

Цель работы: научиться представлять числа в различных системах счисления, научиться выполнять арифметические действия в различных системах счисления.

Студент должен

знать:

правила выполнения арифметических операций в позиционных системах счисления;

уметь:

переводить числа из одной системы счисления в другую.

 

Теоретическое обоснование.

 

Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную системы счисления. Триады. Тетрады.

 

Правило: Чтобы перевести целое двоичное число в восьмеричную (8=2³) систему счисления необходимо:

1. разбить данное число справа налево на группы по 3 цифры в каждой;

2. рассмотреть каждую группу и записать ее соответствующей цифрой восьмеричной системы счисления.

10-я 8-я 16-я

10-я 8-я 16-я 10 (A)     11 (B)     12 (C)     13 (D)     14 (E)     15 (F)       *() – 16-я система счисления.

Пример 1. Перевести число 11101010₂ в восьмеричную систему счисления. Решение: 011 101 010

3 5 2

Ответ: 11101010₂ = 352₈

 

Правило: Чтобы перевести целое двоичное число в шестнадцатеричную (16=2⁴) систему счисления необходимо: 1. разбить данное число справа налево на группы по 4 цифры в каждой;

2. рассмотреть каждую группу и записать ее соответствующей цифрой шестнадцатеричной системы счисления.

Пример 2. Перевести число 111000102 в шестнадцатеричную систему счисления. Решение: 1110 0010

E 2

Ответ: 11100010₂ = Е2₁₆

 

Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную систему счисления

Правило: Для того, чтобы восьмеричное (шестнадцатеричное) число перевести в двоичную систему счисления, необходимо каждую цифру этого числа заменить соответствующим числом, состоящим из 3 (4) цифр двоичной системы счисления.

Пример 3. Перевести число 523₈ перевести в двоичную систему счисления. Решение: 5 2 3

101 010 011

Ответ: 523₈ = 101010011₂

 

Пример 4. Перевести число 4ВА3516 перевести в двоичную систему счисления. Решение: 4 В А 3 5

0100 1011 1010 0011 0101

Выполнение арифметических действий в разных системах счисления.

Рассмотрим основные арифметические операции: сложение, вычитание. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.

Для выполнения арифметических операций в системе счисления с основанием P необходимо иметь соответствующие таблицы сложения и умножения. Для P = 2, 8 и 16 таблицы представлены ниже.

Р =2

+

*

 

Р =8

+

*

 

Р =16

+

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

A

B

C

D

E

F

B

B

C

D

E

F

1A

C

C

D

E

F

1A

1B

D

D

E

F

1A

1B

1C

E

E

F

1A

1B

1C

1D

F

F

1A

1B

1C

1D

1E

 

 

*

A

B

C

D

E

F

A

B

C

D

E

F

A

C

E

1A

1C

1E

C

F

1B

1E

2A

2D

C

1C

2C

3C

A

F

1E

2D

3C

4B

C

1E

2A

3C

4E

5A

E

1C

2A

3F

4D

5B

1B

2D

3F

5A

6C

7E

A

A

1E

3C

5A

6E

8C

B

B

2C

4D

6E

8F

9A

A5

C

C

3C

6C

9C

A8

B4

D

D

1A

4E

5B

8F

9C

A9

B6

C3

E

E

1C

2A

7E

8C

9A

A8

B6

C4

D2

F

F

1E

2D

3C

4B

5A

A5

B4

C3

D2

E1

 

Пример 1. Сложим числа 15 и 6 в различных системах счисления.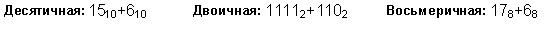

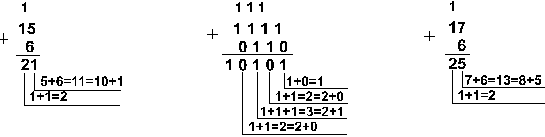
Шестнадцатеричная: F₁₆+6₁₆

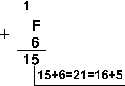
Ответ: 15+6 = 21₁₀ = 10101₂ = 25₈ = 15₁₆.
Пример 2. Сложим числа 15, 7 и 3.

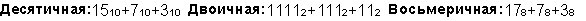
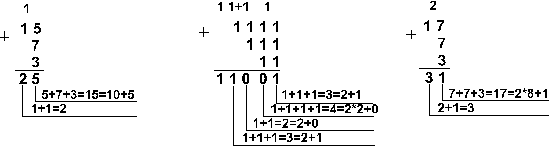
Шестнадцатеричная: F₁₆+7₁₆+3₁₆

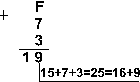
Ответ: 5+7+3 = 25₁₀ = 11001₂ = 31₈ = 19₁₆.

 

Пример 3. Сложим числа 141,5 и 59,75.

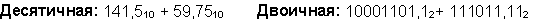
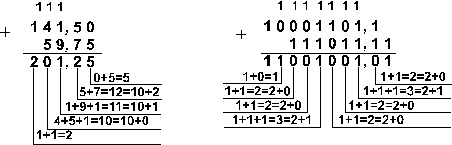
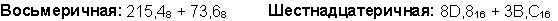
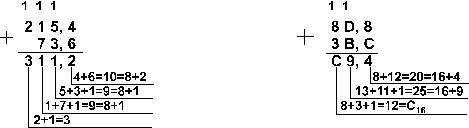
Ответ: 141,5 + 59,75 = 201,25₁₀ = 11001001,01₂ = 311,2₈ = C9,4₁₆

 

Ход работы:

1. Рассмотреть предложенные примеры;

2. Выполнить практическое задание по вариантам;

3. Оформить отчет.

4. Ответить на контрольные вопросы по указанию преподавателя.

 

 

Практические задания:

Вариант 1.

Задание №1.

Переведите числа.

а) 1011011₂ в восьмеричную; б) 517₈ в двоичную; в) 1F₁₆ в двоичную;

Задание №2.

Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения:
а) 1011101₂ и 1110111₂; б) 437₈ и 675₈; в) 5A1₁₆ и 27F₁₆;

Задание №3.

Вычтите:

а) 10100₂-111₂ б) 230₈- 155₈ в) 31₁₆- 1А₁₆

Задание №4.

Умножьте:

а) 101₂*11₂ б) 23₈* 55₈ в) 3В₁₆*8А₁₆

Вариант 2.

Задание №1.

Переведите числа.

а) 10110111₂ в шестнадцатеричную; б) 1010₈ в двоичную; в) ABC₁₆ в восьмеричную;

Задание №2.

Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения:

а) 1011101₂ и 101011₂; б) 165₈ и 37₈; в) 1А9₁₆ и 2ВC₁₆;

Задание №3.

Вычтите:

а) 1101₂-1011₂ б) 102₈-47₈ в) 2А30₁₆- F9E₁₆

 

Задание №4.

Умножьте:

а) 101₂*11₂ б) 152₈*47₈ в) 2А₁₆* FE₁₆

Вариант 3.

Задание №1. Переведите числа.

а) 11100001₂ в восьмеричную; б) 1234₈ в шестнадцатеричную; в) 1010₁₆ в двоичную;

Задание №2.

Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения:

а) 10111₂ и 11011₂; б) 575₈ и 146₈; в) A5B₁₆ и E7F₁₆;

Задание №3.

Вычтите:

а) 10010₂-1111₂ б) 567₈ -101₈; в) B92₁₆-19F₁₆

 

Задание №4.

Умножьте:

а) 110₂*11₂ б) 56₈ *71₈; в) B2₁₆*1F₁₆

 

Вариант 4.

Задание №1. Переведите числа.

а) 1000110₂ в шестнадцатеричную; б) 34₈ в двоичную; в) А4₁₆ в восьмеричную;

Задание №2.

Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения:

а) 1011111₂ и 110101₂; б) 617₈ и 407₈; в)2 E9₁₆ и 5F₁₆.

Задание №3.

Вычтите:

а) 111011₂- 10001₂ б) 3001₈-1654₈ в)5678₁₆- ABC₁₆

Задание №4.

Умножьте:

а) 101₂*11₂ б) 301₈*14₈ в)58₁₆*AC₁₆

 

Вариант 5.

Задание №1. Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы:

а) 11010011₂ в восьмеричную; б) 1231₈ в шестнадцатеричную; в) 1DE₁₆ в двоичную.

Задание №2.

Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения:

а)1100101₂ и 11010₂ б)562₈ и 127₈ и) А12₁₆ и FDA₁₆

Задание №3.

Вычтите:

а) 10100₂-1101₂ б)123₈-56₈ в)A2D₁₆-17F₁₆

Задание №4.

Умножьте:

а) 101₂*101₂ б)23₈*56₈ в)A2₁₆*1F₁₆

 

Содержание отчета:

1. Название и цель работы.

2. Результат выполнения практических заданий.

3. Ответы на контрольные вопросы.

 

Контрольные вопросы.

1. Что такое триада?

2. Что такое тетрада?

3. Правило перевода двоичного числа в восьмеричное число.

4. Правило перевода двоичного числа в шестнадцатеричное число.

5. Правило перевода восьмеричного числа в двоичное число.

6. Правило перевода шестнадцатеричного числа в двоичное число.

7. Какое наибольшее десятичное число можно записать тремя цифрами:

- в двоичной системе;

- в восьмеричной системе;

- в шестнадцатеричной системе?

 

 

Литература.

Основные источники (ОИ):

Таблица 2б

Номер п/п	Автор	Наименование	Издательство, год издания
ОИ1	И. И. Сергеева	Информатика Режим доступа: https://znanium.com/ bookread2.php?id=517652	НИЦ ИНФРА-М, 2016
ОИ2	М. С. Цветкова	Информатика. [Текст]: Учебное пособие для студ. учреждений среднего профессионального образования	М.: Академия, 2017

Дополнительные источники (ДИ):

Таблица 2в

№ п/п	Автор	Наименование	Издательство, год издания
ДИ 1	В. Д. Колдаев	Сборник задач и упражнений по информатике Режим доступа: https://znanium.com/ bookread2.php?id=504814	ИНФРА-М, 2015
ДИ 2	Е. А. Колмыкова	Информатика. [Текст]: Учебное пособие для студ. учреждений среднего профессионального образования	М.: Академия, 2014
ДИ 3	Н. Г. Плотникова	Информатика и информационно-коммуникационные технологии (ИКТ) Режим доступа: https://znanium.com/ bookread2.php?id=433676	ИНФРА-М, 2014
ДИ4	Р. Ю Царев	Программные и аппаратные средства информатики Режим доступа: https://znanium.com/ bookread2.php?id=550017	Краснояр.: СФУ, 2015