УРОК 12. Понятие плоскости и ее обозначения
ЧТО СДЕЛАТЬ?!
ЗАПИСАТЬ ВСЕ СПОСОБЫПОСТРОЕНИЯ ПЛОСКОСТИ
СКОПИРОВАТЬ РИСУНКИ
РЕШИТЬ ЗАДАЧУ.
Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве. В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью. Прямые и точки, размещенные в пространстве, мы будем обозначать аналогично размещенным на плоскости – с помощью строчных и прописных латинских букв (B, A, d, q B, A, d, q и др.) Если в условиях задачи у нас есть две точки, которые расположены на прямой, то можно выбрать такие обозначения, которые будут соответствовать друг другу, например, прямая DB и точки D и B.
Чтобы обозначить плоскость на письме, традиционно используются маленькие греческие буквы, например, α, γ или π. Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм. 
Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга.
Рассмотрим отдельные случаи.
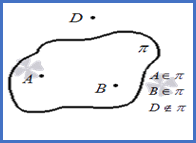
Как могут располагаться плоскость и точка друг относительно друга Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:
|
|
Определение 1 В любой плоскости есть точки. Такой вариант расположения также называется прохождением плоскости через точку. Чтобы обозначить это на письме, используется символ ∈. Так, если нам нужно записать в буквенном виде, что через точку A проходит некая плоскость π, то мы пишем: A ∈ π.
Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.
Определение 2 Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.
Зная это правило, можно ввести новое обозначение плоскости. Вместо маленькой греческой буквы мы можем использовать названия точек, лежащих в ней, например, плоскость АВС
Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:
Определение 3 Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости. Выше мы уже отмечали, что для обозначения плоскости в пространстве будет достаточно трех точек, а четвертая может находиться как в ней, так и вне ее. Если нужно обозначить отсутствие принадлежности точки к заданной плоскости на письме, то используется знак ∉. Запись вида A∉π правильно читается как «точка A не принадлежит плоскости π» Графически последнюю аксиому можно представить так:
Как задать плоскость в пространстве
1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.
|
|
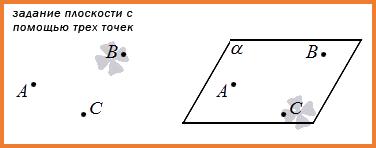
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:
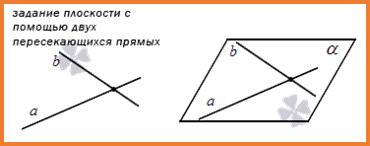
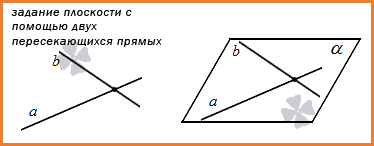
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость.

ЗАДАЧА.
Точки А, В, С,D в одной плоскости а). Могут ли какие-то три из них лежать на одной прямой в). Могут ли прямые АВ и СD пересекаться? Ответ обосновать.