Методы экспертных оценок

В последнее время все более широко применяют при решении различных научных, технико-экономических и производственных задач, а также задач прогнозирования методы коллективной экспертной оценки - метод «мозговой атаки» и метод Делфи. Суть экспертных оценок состоит в том, что группе специалистов-экспертов ставится ряд вопросов, касающихся развития данного технического направления или предполагаемого объекта техники. Суждение о прогнозе возникает после соответствующей обработки ответов экспертов.

Метод мозговой атаки или мозгового штурма относится к так называемому зависимому интеллектуальному эксперименту, в ко­тором участвует экспертная группа из 15—20 чел., причем после­дующее предложение любого члена группы вносится с учетом вы­сказывания предшественников и запрещается критика. Эффектив­ность дискуссии оценивается не по критическим замечаниям, а по числу новых идей, выявленных в процессе обсуждения про­блемы.

В отличие от метода мозговой атаки метод Дельфы может быть назван независимым интеллектуальным экспериментом, поскольку каждый эксперт высказывает свое мнение независимо от мнения своих коллег. При этом поощряется изолированность экспертов, соблюдается профессиональная тайна письменного диалога между прогнозистом и каждым экспертом, что способствует исключению влияния авторитетов и «давления» на эксперта.

Различают четыре основные разновидности метода Дельфы: простой ранжировки (метод предпочтения), задания весовых коэффициентов, последовательных сравнений, парных сравнении. Рассмотрим суть каждого из перечисленных методов и методику обработки результатов экспертизы. Метод простой ранжировки заключается в том, что каждо­го эксперта просят расположить признаки в порядке предпочтения. Цифрой 1 (или циф­рой, соответствующей номеру последнего признака) обозначается наиболее важный признак, цифрой 2 (или цифрой, соответствующей номеру предпоследнего признака) — следу­ющий за ним по важности и т. д.

Таблица 1

Таблица рядов предпочтения данного признака другим

Признак	Эксперт
		…	i	m
			…
			…
…	…	…	…	…	…
			…
			…

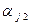
Полученные данные для удобства приводят в виде табл. 1. Определив с помощью известных методов средний ранг (сред­нее значение) каждого j-го признака

= , (1)

где — порядок предпочтения данного признака; — число экспертов, оценивающих j-й признак; i—номер эксперта; j—но­мер признака, получают обобщенное мнение экспертов по каждо­му признаку. При этом степень важности признака тем выше, чем меньше (в первом случае) или больше (во втором) среднее зна­чение ранга.

В связи с тем, что от разных экспертов можно получить весьма разные оценки одного и того же фактора, особое внимание обра­щается на согласованность оценок.

Согласованность мнений экспертов оценивают с помощью ко­эффициента конкордации W, который представляет собой отноше­ние суммы квадратов отклонений S индивидуальных оценок экспертов к максимально возможной сумме квадратов отклоне­ний Smах. При этом

, (2)

где - общая средняя всех оценок;

. (3)

С учетом выражений (2) и (3) коэффициент конкордации

Коэффициент W может принимать значения от 0 до 1. При пол­ной согласованности мнений экспертов коэффициент конкордации равен единице, при полном разногласии—нулю. Наиболее реаль­ным является случай частичной согласованности мнений экспер­тов.

Достоинствами метода простой ранжировки является сравни­тельная простота процедуры получения оценок и небольшое (по сравнению с другими методами экспертных оценок) число экспер­тов.

Метод задания весовых коэффициентов заключается в присвое­нии каждому из признаков весовых коэффициентов, которые могут быть представлены двумя способами:

всем признакам назначают весовые коэффициенты так, чтобы сумма коэффициентов была равна какому-либо фиксированному числу (например, единице, десяти, ста и т. д.); наиболее важному из всех признаков придают весовой коэффициент, равный какому-то фиксированному числу, а всем остальным — коэффициенты, равные долям этого числа.

Обобщенное мнение экспертов получают также с помощью среднего статистического значения j-го признакапо выражению (1), где под понимают весовой коэффициент, присвоенный i-м экспертам j-му признаку. При этом, чем больше ,тем важнее признак. Однако сказать что-либо о согласованности мнений экс­пертов невозможно, поскольку неизвестно, каким должно быть распределение в идеальном случае. Фактически метод задания весовых коэффициентов является методом так называемой слож­ной ранжировки.

Метод последовательных, сравнений заключается в следующем:

эксперт упорядочивает все признаки в порядке уменьшения их значимости: ;присваивает первому признаку зна­чение, равное единице, остальным назначает коэффициенты в до­лях единицы; сравнивает значение первого признака с суммой всех остальных, при этом возможны три варианта:

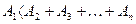
Эксперт выбирает наиболее соответствующий, по его мнению вариант и приводит в соответствие с ним оценку первого признака; сравнивает значе-ние первого признака с суммой всех последующих за вычетом последнего признака и т. д.; повторяет процедуру до сравнения с

После того как эксперт уточняет оценку первого признака в соответствии с выбранным им неравенством из трех возможных ; ; он переходит к уточнению оценки признака по той же схеме.

Преимущество метода последовательных сравнений перед другими состоит в том, что эксперт в процессе оценки важ­ности признаков сам анализирует свои оценки; недостаток—в сложности и громоздкости прово­димой работы.

Таблица 2

Форма матрицы парных сравнений

Признак	A	B	C		N
А		А:В	А:С		А:N
В	B:А		В:С		B:N
С	С:А	С:В			C:N
N	N:А	N:В	N:С

Метод парных сравнений применяют при наличии большого числа альтернатив. Согласно этому методу все признаки попарно сравнивают между собой и на основании оценок парных сравне­ний путем дальнейшей обработки находят оценки каждого приз­нака. Для облегчения процедуры попарного сравнения признаков обычно составляют таблицу матрицы парных сравнений (табл. 2).

Каждый эксперт, заполняющий такую матрицу, должен проста­вить на пересечении сравниваемых факторов их отношение: в пер­вой клетке первой строки (сравнение признака самого с собой) эксперт пишет единицу, во второй — результат сравнения первого признака со вторым, в третьей — результат сравнения первого признака с третьим и т. д. Во второй строке эксперт записывает в первой клетке результат сравнения второго признака с первым, во второй — единицу, в третьей — сравнение второго признака с третьим и т. д. При этом оценки не должны быть больше едини­цы — наиболее важный признак (или показатель) из двух сравни­ваемых приравнивается единице, второй оценивается в долях единицы. Как видно, половина таблицы, расположенная выше диаго­нали, является отражением нижней половины. Поэтому обычно заполняют только одну половину табл. 2, а затем ответы экспер­тов представляют в следующем виде:

i11 i12 i13 … i1n

i22 i23 … i2n,

i33 … i3n

где i1n=А/N.

В случаях, когда каждую пару факторов сравнивают одно­кратно, число сравнений I=n(n — 1)/2, где n—общее число фак­торов.

Так, если имеются три альтернативы, то каждый эксперт должен произ-вести I3 =3 (3-1)/2=3 сравнения. Это значит, что он должен сравнить аль-тернативу I с альтернативами II и III, затем альтернативу II с альтернативой III.

Если процедура парных сравнений выполняется несколькими экспертами, то в результате сложения одноименных элементов частных матриц составляют суммарную матрицу, отражающую предпочтения всех экспертов:

.

В этой матрице ,…., где m—число экспертов; , оценки соответственно1, 2,…, j,…, m - го экспертов; , ,…, - суммарные оценки матрицы, данные всеми экспертами.

После этого определяют средний ранг фактора, полученного от каждого эксперта и от всех экспертов, и, сравнивая значения полученных рангов, делают заключение о степени важности каж­дого из рассматриваемых факторов.

Определяя дисперсию суммарной матрицы и сравнивая ее с максимально возможной с таким же числом элементов, опреде­ляют согласованность мнений экспертов, при этом, чем ближе дисперсия суммарной матрицы к максимально возможной диспер­сии, тем выше согласованность мнений. Метод парных сравнений позволяет провести статистически обоснованный анализ согласо­ванности мнений экспертов, выявить, случайны ли полученные оценки.