Геометрическая интерпретация комплексных чисел.

Еометрическая интерпретация комплексного числа

Всякое комплексное число z = (x, y) можно изобразить как точку на плоскости с координатами x и y. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy - мнимой.

Расстояние r точки z от нулевой точки, т. е. число

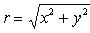
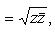
называется модулем комплексного числа z и обозначается символом | z |.

Число

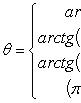
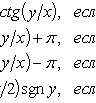
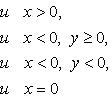
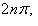
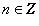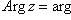
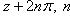
называем аргументом комплексного числа z и обозначаем символом θ = arg z. При заданном r углы, отличающиеся на , соответствуют одному и тому же числу. В этом случае записываем 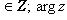называем главным значением аргумента.

Числа r и θ называют полярными координатами комплексного числа z. В этом случае

z = (x, y) = (r cos θ, r sin θ) = r (cos θ + i sin θ)

называется тригонометрической формой комплексного числа.

Если z ₁ = (r ₁ cos θ ₁, r ₁ sin θ ₁), z ₂ = (r ₂ cos θ ₂, r ₂ sin θ ₂), то

z ₁ z ₂ = (r ₁ r ₂ cos(θ ₁ + θ ₂), r ₁ r ₂ sin(θ ₁ + θ ₂)),

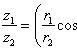
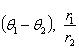
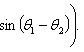
Для n -й степени числа z = (r cos θ, r sin θ) формула приобретает вид zⁿ = (rⁿ cos nθ, rⁿ sin nθ).

При r = 1 соотношение приобретает вид zⁿ = (cos nθ, sin nθ) и называется формулой Муавра.

Корень n -й степени из комплексного числа z имеет n различных значений, которые находятся по формуле

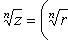
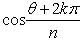
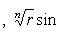
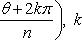
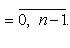(1)

 

решения некоторых задач

 

Геометрическая интерпретация комплексного числа

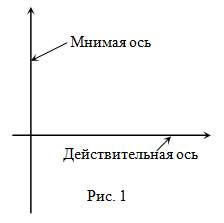
Комплексные числа изображаются на так называемой комплексной плоскости. Ось, соответствующая в прямоугольной декартовой системе координат оси абсцисс, называется действительной осью, а оси ординат - мнимой осью (рис. 1).

Комплексному числу 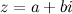будет однозначно соответствовать на комплексной плоскости точка 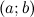: 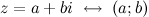(рис. 2). То есть на действительной оси откладывается действительная часть комплексного числа, а на мнимой - мнимая.

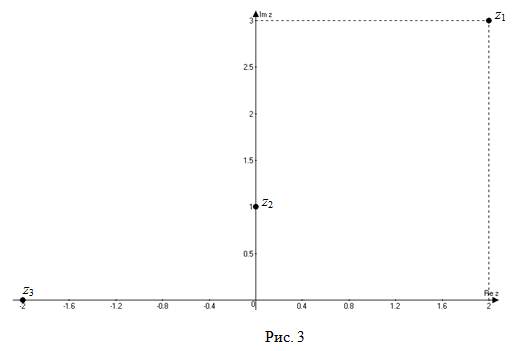
Например. На рисунке 3 на комплексной плоскости изображены числа 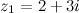, 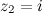и .

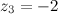Модуль комплексного числа

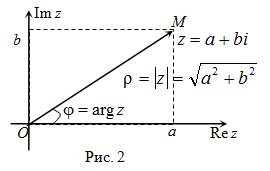
Комплексное число также можно изображать радиус-вектором 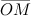(рис. 2). Длина радиус-вектора, изображающего комплексное число 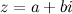, называется модулем этого комплексного числа.

Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чиселравны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.

Модуль вычисляется по формуле:

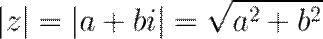
То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.

Пример

Задание. Найти модуль комплексного числа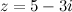

Решение. Так как 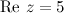, , 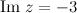то искомое значение

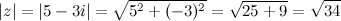
Ответ.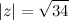

Замечание

Иногда еще модуль комплексного числа обозначается как или .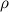

Аргумент комплексного числа

Угол 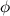между положительным направлением действительной оси и радиус-вектора 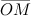, соответствующим комплексному числу 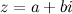, называется аргументом этого числа и обозначается .

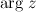Аргумент 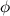комплексного числа 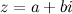связан с его действительной и мнимой частями соотношениями:

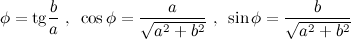
На практике для вычисления аргумента комплексного числа обычно пользуются формулой:

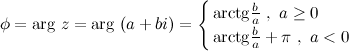
Пример

Задание. Найти аргумент комплексного числа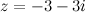

Решение. Так как 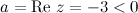, то в выше приведенной формуле будем рассматривать вторую строку, то есть

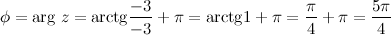
Ответ.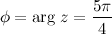

Аргумент действительного положительного числа равен 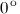, действительного отрицательного - 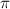или 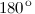. Чисто мнимые числа с положительной мнимой частью имеют аргумент равный 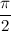, с отрицательной мнимой частью - .

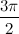У комплексно сопряженных чисел аргументы отличаются знаком (рис. 3).

 

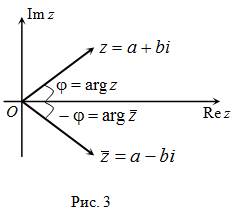
Читать дальше: комплексно сопряженные числа.

 

 

Геометрическая интерпретация комплексных чисел.

Множество действительных чисел можно рассматривать как подмножество комплексных чисел, у которых $Im z= 0.$

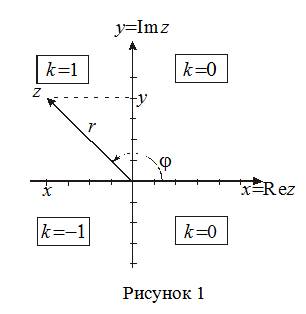
Комплексное число z=x+iy изображают на координатной плоскости Oxy точкой с координатами (x;y). Эта плоскость называется комплексной плоскостью C (рисунок 1), ось Ox называется действительной осью, а ось Oy – мнимой осью. Таким образом, действительному числу z=x+0i=x отвечает точка на действительной оси, а мнимому числу z=0+iy=iy– точка на мнимой оси.

Можно также изображать комплексное число в виде радиус-вектора {x,y} и определять его, задавая его длину r и угол φмежду осью Ox и вектором.

Длина этого вектора называется модулем комплексного числа

|z|=r=x2+y2−−−−−−−√≥0,

а угол φ называется аргументом комплексного числа и обозначается Argz. Аргумент определяется с точностью до слагаемого 2πk(k=0,±1,±2,±3,...) и для положительных значений отсчитывается от оси Oxдо вектора против часовой стрелки, а для отрицательных значений – по часовой стрелке.

Значение аргумента, который принадлежит интервалу (−π,π], называется главным значением аргумента и определяется argz. Главное значение аргументу числа x+iy можно вычислять по формуле φ=argz=arctg(yx)+kπ, где k=0, если z находится в первой или четвертой четвертях, k=1, если z находится во второй четверти, k=−1, если z находится в третей четверти. Если x=Rez=0, то φ=π/2, когда y=Imz>0 и φ=−π/2, когда y=Imz<0. плоскость называется комплексной плоскостью C (рисунок 1), ось Ox называется действительной осью, а ось Oy – мнимой осью. Таким образом, действительному числу z=x+0i=x отвечает точка на действительной оси, а мнимому числу z=0+iy=y− точка на мнимой оси.