Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Решить квадратное уравнение.
1.508. z2+2z+5=0.
Решение.
D=22−4⋅1⋅5=4−20=−16
z1=−2+−16√2=−2+16√−1√2=−2+4i2=−1+2i;
z2=−2−−16√2=−2−16√−1√2=−2−4i2=−1−2i.
Ответ: z1=−1+2i; z2=−1−2i.
1.509. 4z2−2z+1=0.
Решение.
D=(−2)2−4⋅4⋅1=4−16=−12
z1=2+−12√8=2+12√−1√8=2+23√i8=14+3√4i;
z2=2−−12√8=2−12√−1√8=2−23√i8=14−3√4i.
Ответ: z1=14+3√4i; z2=14−3√4i.
Решить биквадратное уравнение
1.516. z4+18z2+81=0.
Решение.
Сделаем замену переменных:
t=z2.
Получаем квадратное уравнение:
t2+18t+81=0.
Решим его:
D=(18)2−4⋅1⋅81=324−324=0.
t1=−18+02=−9;
t2=−18−02=−9.
Далее сделаем обратную замену:
t1=t2=z21,2=z23,4⇒
⇒−9=z21,2⇒
⇒z1,2=±−9−−−√=±9√−1−−−√=±3i.
Ответ: z1,2=z3,4=±3i.
Домашнее задание
Решить биквадратное уравнение
1.517. z4+4z2+3=0.
Ответ: z1,2=±i z3,4=±3√i.
1.518. z4+9z2+20=0.
Ответ: z1,2=±2i z3,4=±5√i.
Геометрическая интерпретация комплексного числа
Добавить комментарий
Задана плоскость. Зададим на ней декартову систему координат.
Данная плоскость называется комплексной. Ось 
называется вещественной, а ось 
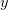— мнимой. На данном рисунке видно, что геометрически комплексное число представляет из себя вектор. Между алгебраической и геометрической интерпретациями комплексного числа существует биекция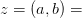 
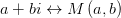
Определение 1
Модулем комплексного числа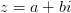 
называется корень разности квадратов его действительной и мнимой частей.
, 
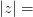
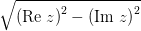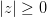
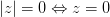
Определение 2
Расстояние между двумя векторами на комплексной плоскости вычисляется по формуле:
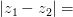
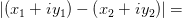
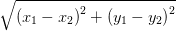
Определение 3
Величина угла, который образует вектор, изображающий данное комплексное число на комплексной плоскости с вещественной осью называется аргументом этого комплексного числа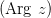 
. Угол, отсчитываемый от оси против часовой стрелки считается положительным, а по часовой — отрицательным.
, 
, 
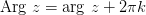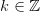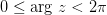, где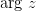 
- главное значение аргумента комплексного числа.
Пример 1
Задание:
Изобразите графически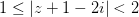 
Решение:
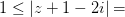
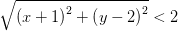
Ответ:
Пример 2
Задание:
Изобразите графически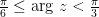 
Ответ:
Литература:
- Белозеров Г.С. Конспект лекций
- Кострикин А.И. Введение в алгебру. Часть I. Основы алгебры. М.:Физико-математическая литература, 2004, стр. 169-170
- Фаддеев Д.К. Лекции по алгебре. М.:Наука, 1984, стр. 31-33
Геометрическая интерпретация комплексных чисел (лекции)
Тест на знание темы: «Геометрическая интерпретация комплексных чисел»
Таблица лучших: Геометрическая интерпретация комплексных чисел (лекции)
| МЕСТО | ИМЯ | ЗАПИСАНО | БАЛЛЫ | РЕЗУЛЬТАТ |
| Иван Чеповский | 02.06.2014 22:58 | 100 % | ||
| Иван Чеповский | 18.05.2014 20:24 | 85.71 % | ||
| Иван Чеповский | 03.06.2014 23:00 | 85.71 % | ||
| Сидоренко | 26.05.2014 12:42 | 71.43 % | ||
| Сидоренко | 26.05.2014 12:44 | 71.43 % | ||
| максимум из 7 баллов |
Поделиться ссылкой:
Что такое "геометрическая интерпретация комплексного числа"? Ответ сокращённый и точный.
Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу z = x + yi ставится в соответствие точка (x, y) координатной плоскости таким образом, что действительная часть комплексного числа представляет собой абсциссу, а коэффициент при мнимой части – ординату точки.
Комплексные числа
Комплексным числом называют выражение вида a + bi, где a и b - вещественные числа, а i - символ, удовлетворяющий соотношению i 2 = – 1. Если z = a + bi, то числа a и b называют соответственно вещественной и мнимою частью числа z (обозначение:
| a = | Re | z |
,
| b = | Im | z |
), а комплексное число a – bi называют числом, сопряженным к числу z (обозначение:
| - z |
). Перемножают комплексные числа по обычным правилам раскрытия скобок и приведения подобных членов, заменяя каждый раз i 2 на – 1, т. е.
|
Каждое вещественное число a можно рассматривать как комплексное число a + 0 i.
Если на плоскости выбрать систему координат, то можно установить взаимно однозначное соответствие между комплексными числами и точками плоскости, при котором числу a + bi соответствует точка с координатами (a, b). При этом умножение на комплексное число z приобретает следующую геометрическую интерпретацию. Пусть r - расстояние от нуля до z, j - угол, на который нужно повернуть вокруг нуля луч, содержащий положительные вещественные числа, чтобы получить луч Oz. Тогда умножение на число z - это композиция гомотетии с коэффициентом r (с центром в нуле) и поворота на угол j. Числа r и j называют соответственно модулем и аргументом числа z (обозначение: r = | z |, j = arg z). По-другому геометрическую интерпретацию произведения комплексных чисел можно сформулировать так: при умножении комплексных чисел их модули перемножаются, а аргументы складываются.
Зная геометрическую интерпретацию комплексных чисел, легко научиться их делить: для этого нужно делить модули и вычитать аргументы. Деление можно ввести также и чисто алгебраически. Для каждого комплексного числа z = a + bi имеет место очевидное равенство
|
Поэтому
| w / z = w | - z | /| z |2 |
.
Тот факт, что произведение комплексных чисел, с одной стороны, вычисляется чисто алгебраически, а с другой стороны, имеет геометрическую интерпретацию, иногда бывает полезным при решении задач планиметрии. Как правило, решение, использующее комплексные числа, в действительности использует только векторы и поворот. Но иногда комплексные числа позволяют взглянуть на теоремы планиметрии с новой точки зрения и, что гораздо важнее, глубже понять их природу.
Очень простую интерпретацию на языке комплексных чисел имеет инверсия с центром в нуле: она отображает число z в число
| R 2/ | - z |
, где R 2 - степень инверсии.
29.20.
Пусть a, b, c, d - комплексные числа, причем углы a 0 b и c 0 d равны и противоположно ориентированы. Докажите, что тогда
| Im | abcd = 0 |
.
Будем говорить, что треугольники ABC и A ¢ B ¢ C ¢ собственно подобны, если существует поворотная гомотетия, которая переводит A в A ¢, B в B ¢, C в C ¢.
29.21.
Докажите, что если треугольники abc и a ¢ b ¢ c ¢ на комплексной плоскости собственно подобны, то
|
29.22.
Докажите, что треугольники abc и a ¢ b ¢ c ¢ собственно подобны, тогда и только тогда, когда
|
29.23.
Пусть a и b - комплексные числа, лежащие на окружности с центром в нуле, u - точка пересечения касательных к этой окружности в точках a и b. Докажите, что u = 2 ab /(a + b).
29.24.
Пусть a - комплексное число, лежащее на единичной окружности S с центром в нуле, t - вещественное число (точка, лежащая на вещественной оси). Пусть, далее, b - отличная от a точка пересечения прямой at с окружностью S. Докажите, что
| - b | = (1 – ta)(t – a) |
.
29.25.
Даны треугольник ABC и прямая l, проходящая через центр O вписанной окружности. Обозначим через A 1 (соответственно B 1, C 1) основание перпендикуляра, опущенного на прямую l из точки A (соответственно B, C), а через A 2 (соответственно B 2, C 2) обозначим точку вписанной окружности, диаметрально противоположную точке касания со стороной BC (соответственно CA, AB). Докажите, что прямые A 1 A 2, B 1 B 2, C 1 C 2, пересекаются в одной точке, и эта точка лежит на вписанной окружности.
29.26.
а) Докажите, что все окружности и прямые задаются уравнениями вида
|
где A и D - вещественные числа, а c - комплексное число. Наоборот, докажите, что любое уравнение такого вида задает либо окружность, либо прямую, либо точку, либо пустое множество.
б) Докажите, что при инверсии окружности и прямые переходят в окружности и прямые.
29.27.
Пусть точки A *, B *, C *, D * являются образами точек A, B, C, D при инверсии. Докажите, что:
а)
| AC AD | : | BC BD | = | A * C * A * D * | : | B * C * B * D * |
;
б) Ð(DA, AC) – Ð(DB, BC) = Ð(D * B *, B * C *) – Ð(D * A *, A * C *).
29.28.
Докажите, что точки, соответствующие комплексным числам a, b, c, лежат на одной прямой тогда и только тогда, когда число
| a – b a – c |
, называемое простым отношением трех комплексных чисел, вещественно.
б) Докажите, что точки, соответствующие комплексным числам a, b, c, d, лежат на одной окружности (или на одной прямой) тогда и только тогда, когда число
| a – c a – d | : | b – c b – d |
, называемое двойным отношением четырех комплексных чисел, вещественно.
29.29 *.
а) Докажите, что если A, B, C и D - произвольные точки плоскости, то AB · CD + BC · AD ³ AC · BD (неравенство Птолемея).
б) Докажите, что если A 1, A 2, … A 6 - произвольные точки плоскости, то
|
|
в) Докажите, что (нестрогое) неравенство Птолемея обращается в равенство тогда и только тогда, когда ABCD - (выпуклый) вписанный четырехугольник.
г) Докажите, что неравенство из задачи б) обращается в равенство тогда и только тогда, когда A 1… A 6 - вписанный шестиугольник.
29.30 *.
Докажите, что если a, b, c и d - длины последовательных сторон выпуклого четырехугольника ABCD, а m и n - длины его диагоналей, то m 2 n 2 = a 2 c 2 + b 2 d 2 – 2 abcd cos (A + C) (Бретшнейдер).
29.31 *.
а) Даны точка X и треугольник ABC. Докажите, что
|
где a, b, c - длины сторон треугольника.
б) На сторонах BC, CA, AB взяты точки A 1, B 1, C 1. Пусть a, b, c - длины сторон треугольника ABC, a 1, b 1, c 1 - длины сторон треугольника A 1 B 1 C 1, S - площадь треугольника ABC. Докажите, что
|
29.32 *.
На сторонах аффинно правильного многоугольника A 1 A 2… An с центром O внешним образом построены квадраты Aj + 1 AjBjCj + 1 (j = 1,…, n). Докажите, что отрезки BjCj и OAj перпендикулярны, а их отношение равно
| æ è | 1 – cos (2p/ n) | ö ø |
.
29.33 *.
На сторонах выпуклого n -угольника внешним образом построены правильные n -угольники. Докажите, что их центры образуют правильный n -угольник тогда и только тогда, когда исходный n -угольник аффинно правильный.
29.34 *.
Вершины треугольника соответствуют комплексным числам a, b и c, лежащим на единичной окружности с центром в нуле. Докажите, что если точки z и w изогонально сопряжены, то
| z + w + abc | - z | - w | = a + b + c |
(Морли).
29.35 *.
Точки Z и W изогонально сопряжены относительно правильного треугольника. При инверсии относительно описанной окружности точки Z и W переходят в Z * и W *. Докажите, что середина отрезка Z * W * лежит на вписанной окружности.
29.36 *.
Точки Z и W изогонально сопряжены относительно правильного треугольника ABC с центром O; M - середина отрезка ZW. Докажите, что Ð AOZ + Ð AOW + Ð AOM = n p (углы ориентированы).