1. Все вершины сечения лежат на ребрах многогранника
2. Все стороны сечения лежат в гранях многогранника
3. В каждой грани многогранника лежит не более одной стороны сечения
Задания с решениями
1.В прямоугольном параллелепипеде  известны ребра:
известны ребра:  , Найдите угол между плоскостями ABC и
, Найдите угол между плоскостями ABC и  .
.
Решение.
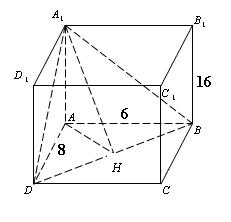
Плоскости ABC и  имеют общую прямую BD. Проведем перпендикуляр AH к BD. По теореме о трех перпендикулярах
имеют общую прямую BD. Проведем перпендикуляр AH к BD. По теореме о трех перпендикулярах  Значит,
Значит,  - линейный угол двугранного угла, образованного плоскостями ABC и
- линейный угол двугранного угла, образованного плоскостями ABC и  . Из прямоугольного треугольника BAD находим:
. Из прямоугольного треугольника BAD находим:
 .Откуда
.Откуда 
Из прямоугольного треугольника  находим:
находим: 
Следовательно. 
Ответ: 
2. В кубе  найдите косинус угла между плоскостями
найдите косинус угла между плоскостями  и
и  .
.
Решение.

Плоскости  и
и  .имеют общую прямую
.имеют общую прямую  . Пусть точка O — центр куба, а M — середина
. Пусть точка O — центр куба, а M — середина  . MO — средняя линия треугольника
. MO — средняя линия треугольника  , поэтому
, поэтому  ||
|| 
 .Но
.Но  , поэтому
, поэтому  . Треугольник
. Треугольник  — равносторонний, М – середина стороны
— равносторонний, М – середина стороны  , следовательно
, следовательно 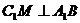 . Значит
. Значит  линейный угол двугранного угла между плоскостями
линейный угол двугранного угла между плоскостями  и
и  .
.
Пусть сторона куба равна а. Найдем стороны треугольника  . Из треугольника
. Из треугольника  , находим
, находим  . Из правильного треугольника
. Из правильного треугольника  ,сторона которого равна
,сторона которого равна  ,находим
,находим 
Поскольку O — середина диагонали  , то
, то  .
.
Теперь применим к треугольнику  теорему косинусов:
теорему косинусов: 
Тогда 
Ответ:  .
.
3. В единичном кубе найдите расстояние от точки А до плоскости
найдите расстояние от точки А до плоскости  .
.
Решение

Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
Чтобы провести перпендикуляр из точки А до плоскости  , проведем через точку А плоскость
, проведем через точку А плоскость  , перпендикулярную плоскости
, перпендикулярную плоскости  :
:

Докажем, что плоскость  перпендикулярна плоскости
перпендикулярна плоскости  .
.
 как диагонали квадрата,
как диагонали квадрата,
 , так как
, так как  перпендикулярна плоскости
перпендикулярна плоскости  и, значит, любой прямой, лежащей в этой плоскости
и, значит, любой прямой, лежащей в этой плоскости
Следовательно, прямая  перпендикулярна двум пересекающимся прямым плоскости
перпендикулярна двум пересекающимся прямым плоскости  и, следовательно, перпендикулярна плоскости
и, следовательно, перпендикулярна плоскости  . Значит, любая плоскость, проходящая через прямую
. Значит, любая плоскость, проходящая через прямую  будет перпендикулярна плоскости
будет перпендикулярна плоскости  , в том числе и плоскость
, в том числе и плоскость  .
.
 – линия пересечения плоскости
– линия пересечения плоскости  и плоскости
и плоскости  .
.
Рассмотрим треугольник  и в плоскости этого треугольника проведем высоту
и в плоскости этого треугольника проведем высоту  к стороне
к стороне  и
и 
Так как плоскости  и
и  взаимно перпендикулярны, то
взаимно перпендикулярны, то  и есть расстояние от точки А до плоскости
и есть расстояние от точки А до плоскости  .
.

Найдем стороны треугольника АРС.
Из треугольника  по теореме Пифагора найдем СР.
по теореме Пифагора найдем СР.

 ,
,  , РО =1
, РО =1
 Подставим в данную формулу найденные значения
Подставим в данную формулу найденные значения

Тогда 
Ответ: 
Способ.
Рассмотрим правильную пирамиду  с основанием
с основанием  и вершиной А
и вершиной А

Расстояние от точки А до плоскости  равно высоте пирамиды.
равно высоте пирамиды.
В основании пирамиды лежит правильный треугольник  стороны которого равны
стороны которого равны  . Боковые ребра пирамиды также равны между собой и равны
. Боковые ребра пирамиды также равны между собой и равны  .
.
Если боковые ребра пирамиды равны между собой, то вершина проецируется в центр О описанной около основания окружности- в нашем случае, в случае правильного треугольника – это точка пересечения, в частности, медиан.

Точка О – точка пересечения медиан правильного треугольника делит медианы в отношении 2:1, считая от вершины.
Тогда 
 найдем по теореме Пифагора из треугольника
найдем по теореме Пифагора из треугольника 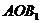

Ответ: 
3 способ.

Рассмотрим правильную пирамиду  с основанием
с основанием  и вершиной А. Она получается, если от единичного куба
и вершиной А. Она получается, если от единичного куба «отрезать» 4 одинаковые пирамиды, объем каждой из которых равен 1/6 объема куба. То есть мы «отрезаем» 2/3 объема куба и остается 1/3.
«отрезать» 4 одинаковые пирамиды, объем каждой из которых равен 1/6 объема куба. То есть мы «отрезаем» 2/3 объема куба и остается 1/3.
Площадь основания пирамиды  равна площади треугольника
равна площади треугольника  и равна
и равна 
Расстояние от точки А до плоскости  равно высоте пирамиды H.
равно высоте пирамиды H.
Получаем:  Откуда
Откуда 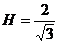
Ответ 
4.В правильной треугольной призме , все ребра которой равны 1, найдите расстояние от точки
, все ребра которой равны 1, найдите расстояние от точки  до прямой
до прямой .
.
Решение
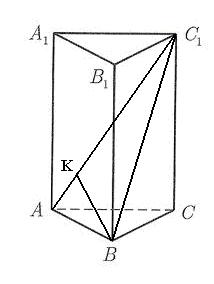
Точки  и
и  лежат в одной плоскости Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на эту прямую. Пусть
лежат в одной плоскости Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на эту прямую. Пусть  .Тогда
.Тогда  и есть искомое расстояние.
и есть искомое расстояние.
Рассмотрим треугольник  и в нем построим
и в нем построим 

Треугольник равнобедренный 

 как диагонали равных квадратов.
как диагонали равных квадратов.  Найдем по теореме Пифагора
Найдем по теореме Пифагора  .
. 


Тогда 
Ответ: 
4.В правильной шестиугольной призме  , все ребра которой равны 1, найти косинус угла между прямыми
, все ребра которой равны 1, найти косинус угла между прямыми  и
и  .
.
Решение
Введем систему координат:
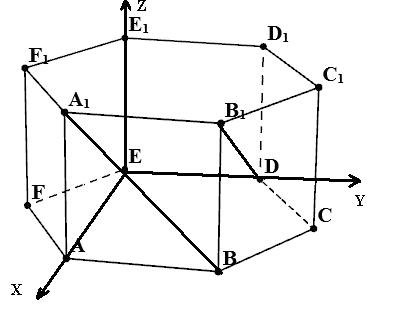
Найдем координаты векторов  и
и  , Для этого найдем координаты точек
, Для этого найдем координаты точек 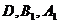 и
и  .
.
В правильном шестиугольнике со стороной 1 найдем  по теореме косинусов.
по теореме косинусов.  .Аналогично
.Аналогично  .
.
Тогда получаем  . Чтобы найти координаты векторов из координат конца вычтем координаты начала. Получим:
. Чтобы найти координаты векторов из координат конца вычтем координаты начала. Получим:
Откуда


 и
и 

Найдем косинус угла  между векторами
между векторами  и
и  .
.
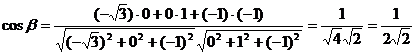

Ответ 

Второй способ.
Построим 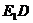 . Так как
. Так как  ,то углы между прямыми
,то углы между прямыми  ,
,  и
и 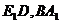 равны, то есть нам надо найти угол
равны, то есть нам надо найти угол 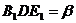

Рассмотрим треугольник  .
.
 как диагональ квадрата со стороной 1.
как диагональ квадрата со стороной 1.
 как диагональ правильного шестиугольника со стороной 1.
как диагональ правильного шестиугольника со стороной 1.
По теореме Пифагора 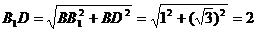
По теореме косинусов из треугольника  получаем:
получаем: 
Подставляя значения, получаем 
 .
.
Откуда  , то есть
, то есть 
Ответ 
