Теорема о единственности предела
Формулировка: Если функция  в точке
в точке  имеет предел, то этот предел единственный.
имеет предел, то этот предел единственный.
Доказательство:
Докажем методом от противного. Предположим, что 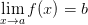 ,
,  ,
,  . Возьмём
. Возьмём  , по определению и свойству окрестности найдётся такая проколотая
, по определению и свойству окрестности найдётся такая проколотая
 -окрестность точки
-окрестность точки  (
(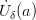 ), в которой одновременно будут выполнятся неравенства
), в которой одновременно будут выполнятся неравенства  ,
, 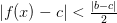 , тогда в точках этой же окрестности
, тогда в точках этой же окрестности 





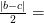
 Получили противоречие
Получили противоречие  . Отсюда, функция
. Отсюда, функция  в точке
в точке  имеет единственный предел.
имеет единственный предел.
№4) Понятие о производной. Геометрический и физический смысл производной.
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной —интегрирование.
Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке.

Физический смысл производной.
Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:
№5)Дифференциал функции. Частные производные, понятие о полном дифференциале.
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
Дифференциал функции y = f (x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так:
 или
или 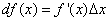 или же
или же 
Формулу для дифференциала функции можно записать в виде: 
Отсюда получаем, что 
Итак, это означает, что производная может быть представлена как обыкновенная дробь - отношение дифференциалов функции и аргумента.
дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.
 В этом и состоит геометрический смысл дифференциала.
В этом и состоит геометрический смысл дифференциала.
6)Применение дифференциала к приближенным вычислениям
Как уже известно, приращение ∆у функции у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство ∆у≈dy, (3) причем это равенство тем точнее, чем меньше ∆х.
Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.
Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (3) широко применяется в вычислительной практике.
В математическом анализе частная производная — одно из обобщений понятия производной на случай функции нескольких переменных.
В явном виде частная производная функции  в точке
в точке  определяется следующим образом:
определяется следующим образом:
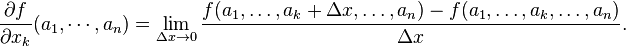
Определение. Полным дифференциалом функции многих переменных называется главная линейная относительно приращений аргументов часть малого полного приращения функции.
Рассмотрим функцию двух переменных n=2; z=f(x,y). Если приращение функции  можно представить в виде
можно представить в виде  ,
,
где  - бесконечно малые функции при
- бесконечно малые функции при 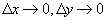 , соответственно, то выражение
, соответственно, то выражение  называется полным дифференциалом функции двух переменных.
называется полным дифференциалом функции двух переменных.
Теорема. Полный дифференциал равен сумме попарных произведений частных производных на дифференциалы соответствующих переменных.

8) Частные и полный дифференциалы функции
Если теперь к частному приращению  применить теорему Лагранжа о конечных приращениях по переменной
применить теорему Лагранжа о конечных приращениях по переменной  , то, считая
, то, считая 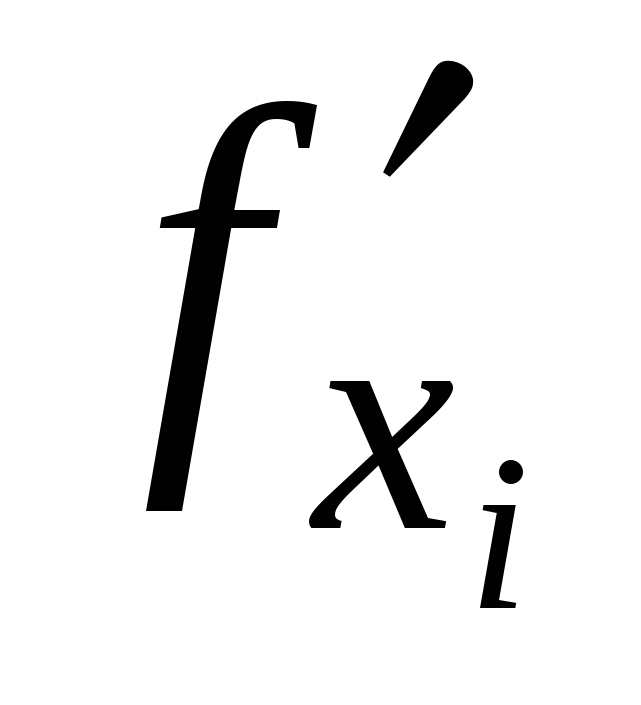 непрерывной, получим следующие соотношения:
непрерывной, получим следующие соотношения:
 где
где  ,
,  – бесконечно малая величина.
– бесконечно малая величина.
Частным дифференциалом функции  по переменной
по переменной  называется главная линейная часть частного приращения
называется главная линейная часть частного приращения 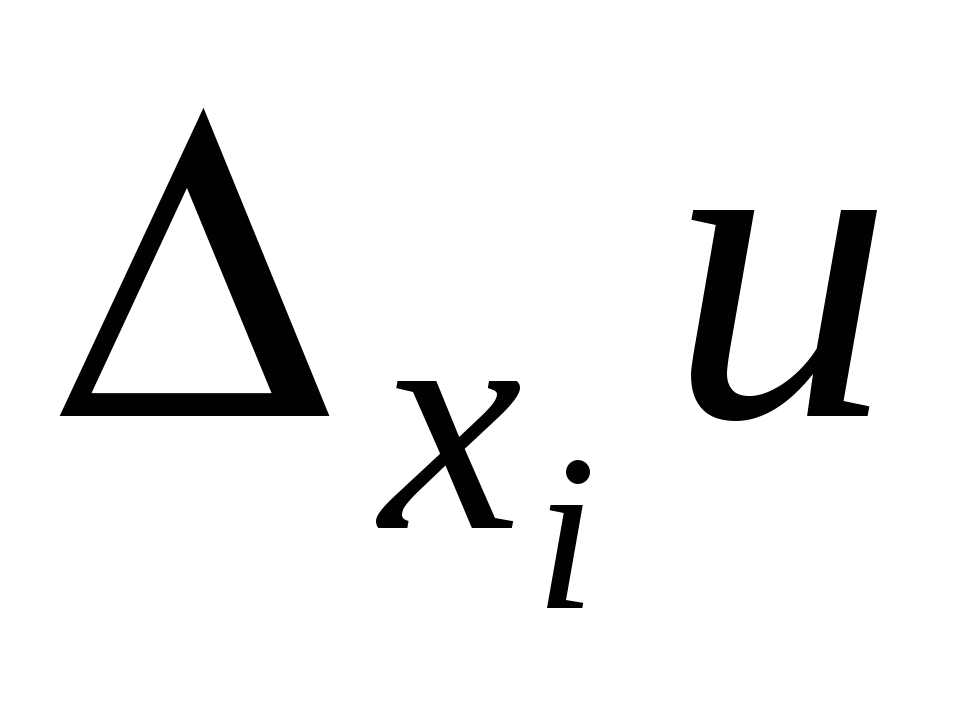 , равная произведению частной производной по этой переменной на приращение этой переменной, и обозначается
, равная произведению частной производной по этой переменной на приращение этой переменной, и обозначается

Очевидно, частный дифференциал отличается от частного приращения на бесконечно малую высшего порядка.
Полным приращением функции многих переменных называется то её приращение, которое она получит, когда мы всем независимым переменным дадим приращение, т.е.
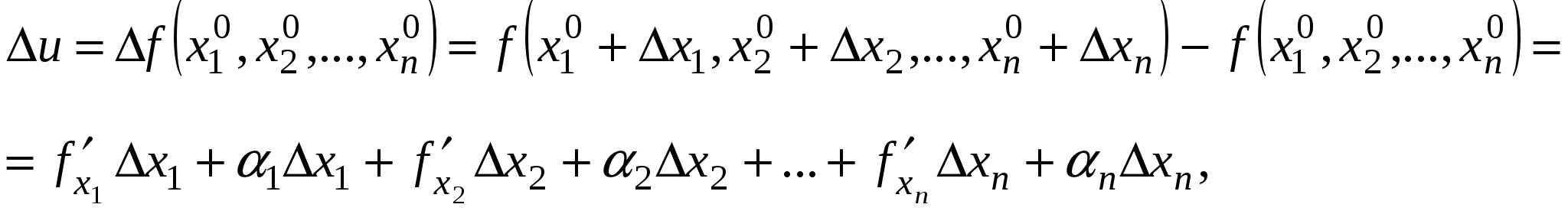
где все  , зависят от
, зависят от  и вместе с ними стремятся к нулю.
и вместе с ними стремятся к нулю.
Под дифференциалами независимых переменных  условились подразумевать произвольные приращения
условились подразумевать произвольные приращения  и обозначать их
и обозначать их  . Таким образом, выражение частного дифференциала примет вид:
. Таким образом, выражение частного дифференциала примет вид: 
Например, частный дифференциал  по
по  определяется так:
определяется так:  .
.
Полным дифференциалом  функции многих переменных
функции многих переменных  называется главная линейная часть полного приращения
называется главная линейная часть полного приращения  , равная
, равная  , т.е. сумме всех её частных дифференциалов:
, т.е. сумме всех её частных дифференциалов:
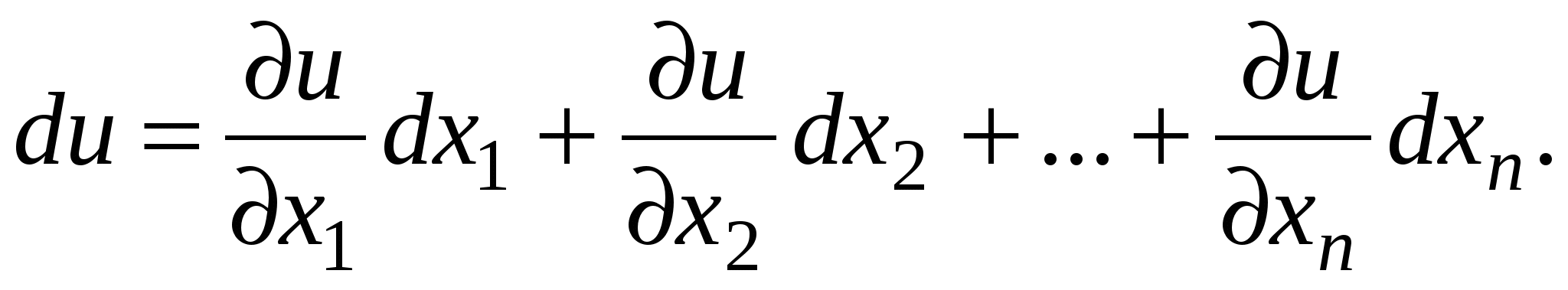
Если функция 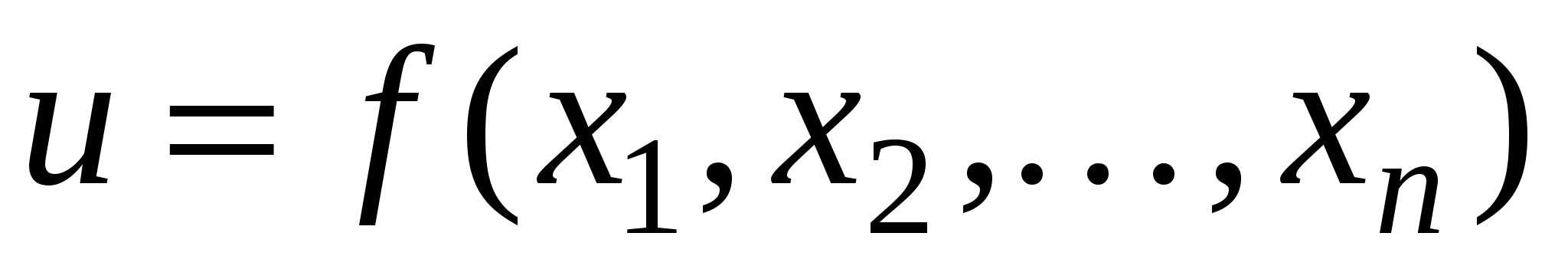 имеет непрерывные частные производные
имеет непрерывные частные производные 
в точке 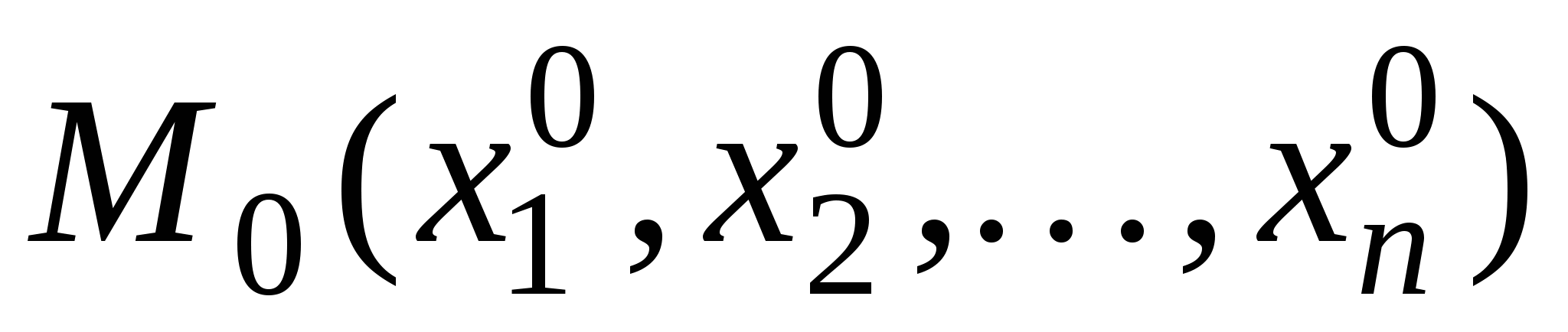 , то она дифференцируема в данной точке.
, то она дифференцируема в данной точке.
При достаточно малом  для дифференцируемой функции
для дифференцируемой функции 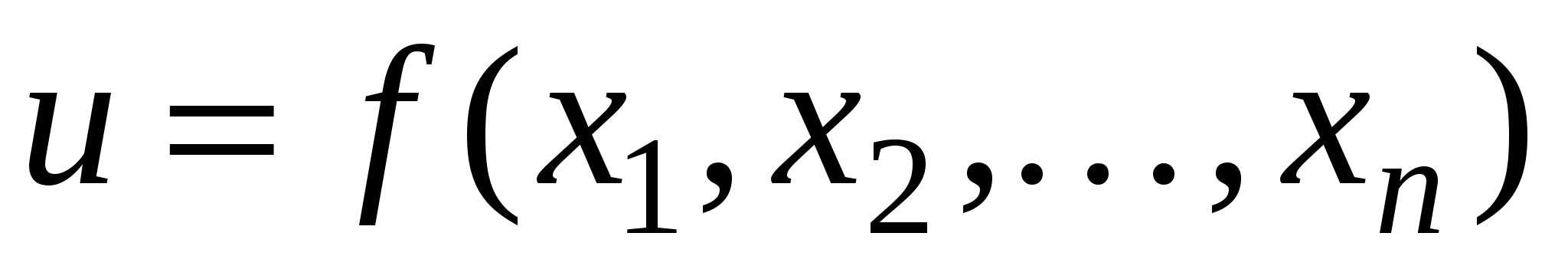 имеют место приближенные равенство
имеют место приближенные равенство 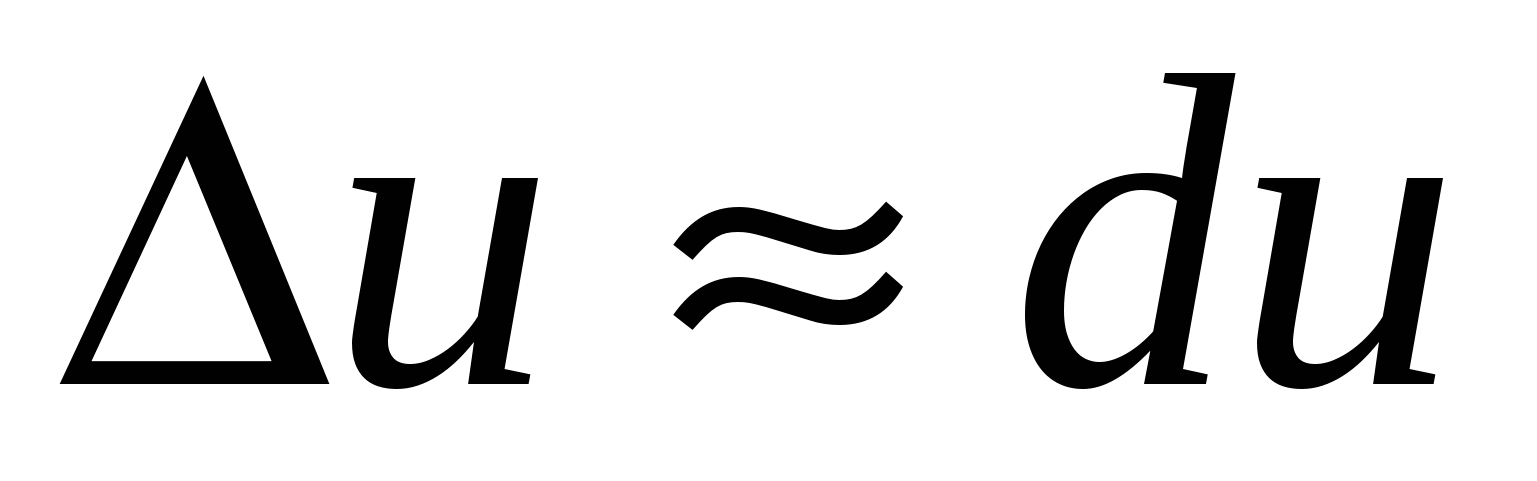 ,
,  ,
,
с помощью которых можно производить приближенные вычисления.
Для дифференциалов функций многих переменных верны все теоремы о свойствах дифференциалов, доказанные для случая функций одной переменной, например: если  и
и  – непрерывные функции переменных
– непрерывные функции переменных 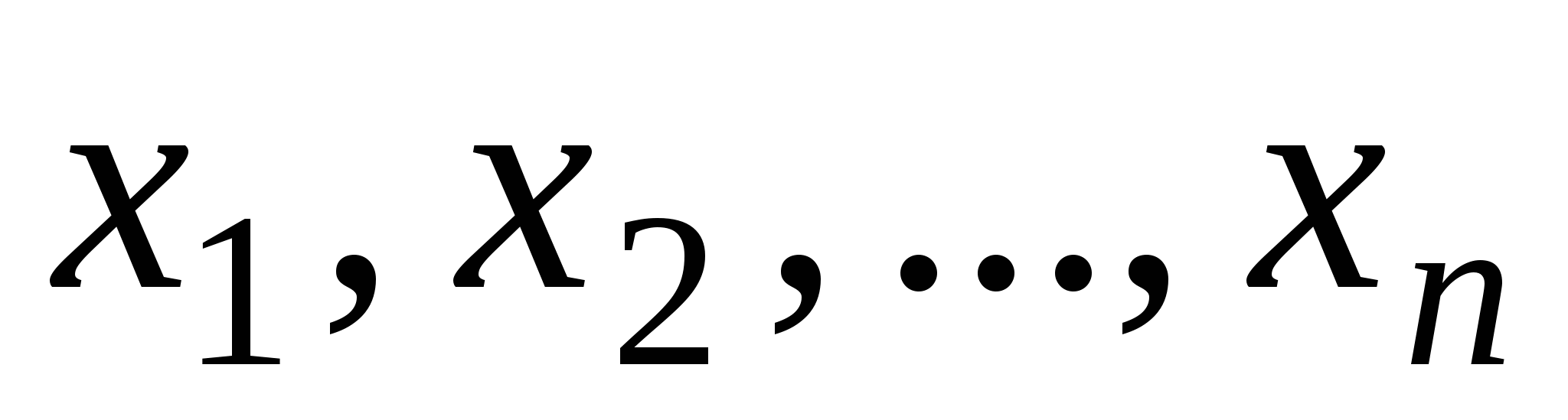 , имеющие непрерывные частные производные по всем переменным, а
, имеющие непрерывные частные производные по всем переменным, а  и
и  – произвольные постоянные, то:
– произвольные постоянные, то:
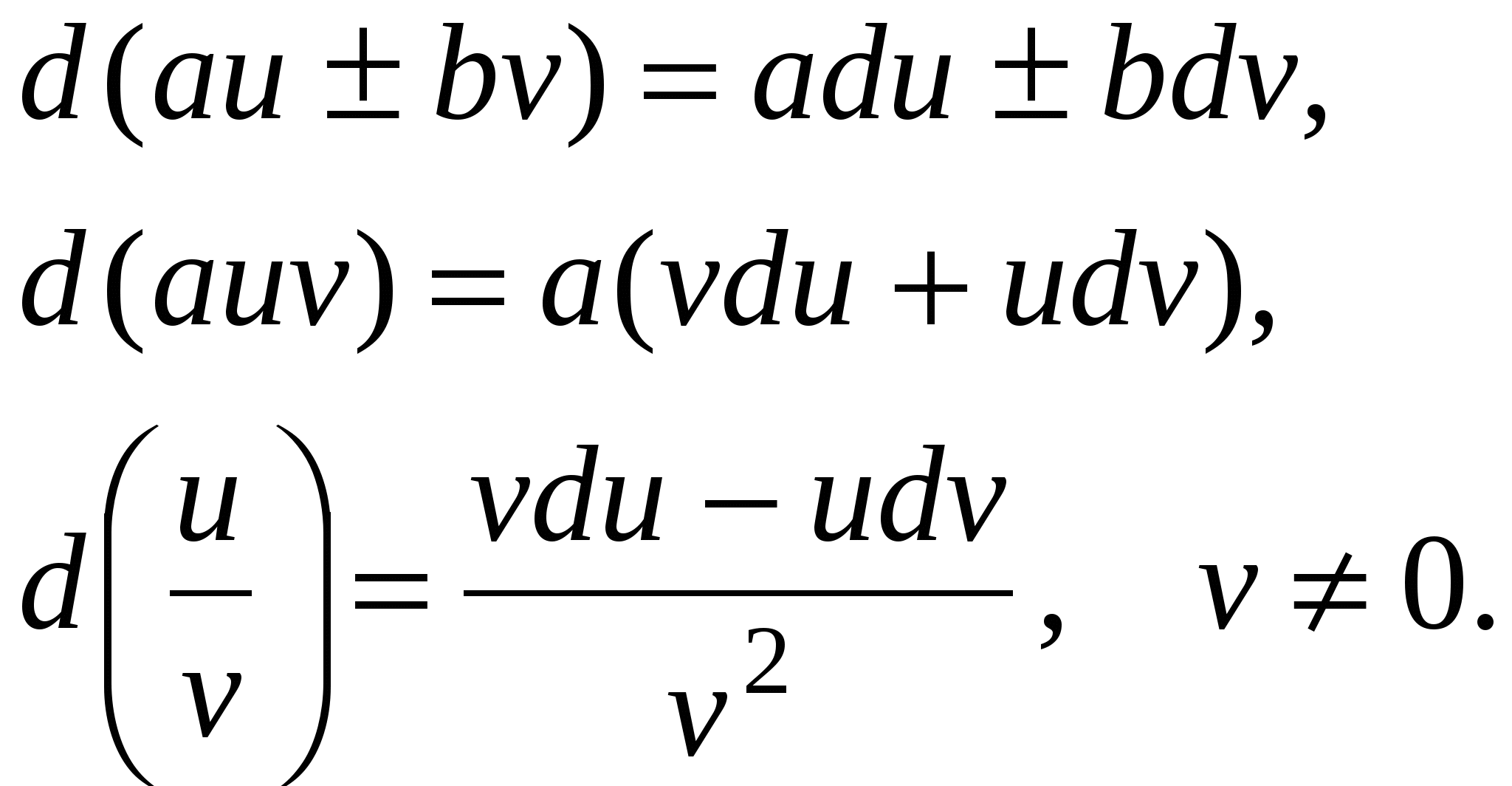
№9)Применение производной для ислледований функций необходимое и достаточное для существования экстремума.
Применение производной к исследованию функций
Функция у = f (х) называется возрастающей (убывающей) на некотором промежутке, если для любых значений x2>x1 этого промежутка выполняется условие f (x2) > f (x1)(f (x2) < f (x1)).
Функция у = f (х) имеет максимум (минимум) в точке x0, если существует такая окрестность точки x0, что для всех x, принадлежащих этой окрестности, выполняется условие f (х) < f (х0)(f (х) > f (х0), х х0.
Максимумы и минимумы функции называются ее экстремумами.
Достаточные условия экстремума.
Если производная при переходе через точку x 0 меняет свой знак с плюса на минус, то x 0 - точка максимума.
Если производная при переходе через точку x 0 меняет свой знак с минуса на плюс, то x 0 - точка минимума.
Интервал, на котором функция возрастает или убывает, называется интервалом монотонности функции. Достаточные признаки монотонности функции.
Если f ’(x) > 0 в каждой точке интервала (a, b), то функция f (x) возрастает на этом интервале.
Если f ’(x) < 0 в каждой точке интервала (a, b), то функция f (x) убывает на этом интервале.
Связь между непрерывностью и дифференцируемостью функции. Если функция f (x) дифференцируема в некоторой точке, то она непрерывна в этой точке..
С л е д с т в и е. Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.
Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.
Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.
Критические точки. Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум
№10 Неопределенный интеграл
Неопределённый интегра́л для функции 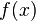 — это совокупность всех первообразных данной функции.
— это совокупность всех первообразных данной функции.
Если функция 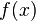 определена и непрерывна на промежутке
определена и непрерывна на промежутке  и
и  — её первообразная, то есть
— её первообразная, то есть 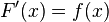 при
при  , то
, то
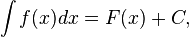
 ,
,
где С — произвольная постоянная.