СИСТЕМЫСЧИСЛЕНИЯ
Система счисления – способ представления чисел, опирающийся на некоторое конечное число знаков, называемых цифрами.
Происхождение наиболее употребительной десятичной системы связано с пальцевым счетом. В России до XVIII в. существовала десятичная система счисления, основанная на буквах алфавита 
, 
, 
и т.д. Начертание этих цифр произошло от греческих букв 
, 
, 
и др. Современная десятичная система основана на десяти цифрах, начертание которых сформировалось в Индии к V в. и пришло в Европу с арабскими рукописями, в связи с чем цифры получили название «арабские». В некоторых странах применяли и другие системы счисления, например, в Китае – пятеричную. Существовавшая в Древнем Вавилоне шестидесятеричная система сохранилась в наши дни в делении часа и градуса угла на 60 минут и минут на 60 секунд. Древние евреи использовали как десятичную, так и двенадцатеричную системы счисления.
В зависимости от способа изображения чисел системы счисления делятся на позиционные и непозиционные. Каждая цифра в числе, записанном в позиционной системе счисления, несет двойную информационную нагрузку:
1) количество;
2) разряд, т.е. позицию, на которой цифра находится в числе.
Например, в десятичном числе 7 313 цифра 3 (та, что левее) означает, что:
1) она находится во втором разряде (отсчет разрядов ведется справа, начиная с нуля), т.е. соответствует разряду сотен;
2) количество этих сотен равно 3.
В любой позиционной системе счисления любое число x может быть представлено в следующем виде:
. (1)
Здесь 
– количество цифр, используемых для записи чисел в данной системе счисления (основание системы счисления);
– числовые коэффициенты, причем положительные значения индексов соответствуют цифрам в целой части числа, а отрицательные – в дробной.
Пример. Десятичное число 7 313, 49 в виде (1) представляется следующим образом:
7 313, 4910 = 7 · 103 + 3 · 102 + 1 · 101 + 3 · 100 + 4 · 10-1 + 9 · 10-2.
Тогда коэффициенты его разложения будут равны
a 3 = 7, a 2 = 3, a 1 = 1, a 0 = 3, a -1 = 4, a -2 = 9.
Приведем некоторые примеры позиционных систем счисления.
Таблица 1
| Система счисления | Основание | Цифры |
| Двоичная | 0, 1 | |
| Восьмеричная | 0, 1, 2, 3, 4, 5, 6, 7 | |
| Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 | |
| Шестнадцатеричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Общепринятая десятичная система счисления оказывается неудобной для технической реализации, поскольку необходимо различные цифры кодировать десятью различными способами. Поэтому для внутреннего представления чисел в компьютере используется двоичная система счисления – в виде сигналов низкого (0) или высокого (1) уровней. Представление чисел в десятичной системе счисления проводится только на этапе получения информации от пользователя и на этапе выдачи результата.
Установим соответствие между записями чисел в системах счисления, представленных в табл. 1.
Таблица 2
| Десятичное число | Двоичное число | Восьмеричное число | Шестнадцатеричное число |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F | |||
Несмотря на удобство технической реализации, двоичная система обладает существенным недостатком – громоздкостью записи чисел. Поэтому для сокращения записи используется восьмеричная или шестнадцатеричная форма записи двоичного числа.
Кроме позиционных систем счисления существуют системы, в которых значение цифры не зависит от той позиции, которую она занимает в числе. Такие системы счисления называются непозиционными. Наиболее известным примером непозиционной системы счисления является римская система. В этой системе используется 7 знаков (I, V, X, L, С, D, М), которые соответствуют следующим величинам:
I (1), V (5), X (10), L (50), С (100), D (500), М (1000).
Например, десятичное число 7 313 в римской системе счисления запишется следующим образом:
MMMMMMMCCCXIII.
Недостатком непозиционных систем счисления является отсутствие формальных правил записи чисел и, соответственно, арифметических действий над ними. Поэтому римские числа используются лишь при нумерации (глав в книгах, веков в истории и др.).
При работе с компьютерами приходится параллельно использовать несколько позиционных систем счисления, поэтому большое практическое значение имеют процедуры перевода чисел из одной системы счисления в другую.
Перевод целого десятичного числа в произвольную р -ичную систему счисления
Для преобразования целого числа x 10 из десятичной системы счисления в р -ичную используется следующий алгоритм:
1) начало;
2) задать число x 10;
3) если x 10 < p, то x 10 = xp (перевод выполнять не нужно) и перейти к шагу 7; в противном случае перейти к шагу 4;
4) разделить x 10на p и записать целую часть m частного и остаток n;
5) записать остаток n с в младший из незаполненных разрядов p -ичного числа;
6) заменить число x 10на m и вернуться к шагу 3;
7) конец.
Пример 1. Перевести число 7 31310 в двоичную, восьмеричную и шестнадцатеричную системы счисления.
| Этап | Перевод в двоичную систему | Перевод в восьмеричную систему | Перевод в шестнадцатеричную систему | ||||||
| x 10 | m | n | x 10 | m | n | x 10 | m | n | |
| 7 313 | 3 656 | 7 313 | 7 313 | ||||||
| 3 656 | 1 828 | ||||||||
| 1 828 | |||||||||
Т.о., 7 31310 = 1 1100 1001 00012 = 16 2218 = 1 C9116.
Перевод дробного десятичного числа в произвольную р -ичную систему счисления
Рассмотрим перевод правильной десятичной дроби (дроби, у которой целая часть равна нулю) 0, y 10в р -ичную систему счисления. В общем случае такой перевод абсолютно точно выполнить не удастся. Почему? Следовательно, перевод числа в p -ичную систему счисления можно выполнить только с определенной точностью 
. Число знаков k после запятой, которые необходимо определить для p -ичного представления дробной части, определяется из соотношения
.
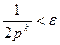Отсюда получаем, что
,
, т.е. 
. (2)
Для преобразования правильной десятичной дроби числа 0, y 10 из десятичной системы счисления в р -ичную используется следующий алгоритм:
1) начало;
2) задать число 0, y 10 и точность ;
3) вычислить по формуле (2) число k р -ичных разрядов, требуемых для записи дробной части;
4) умножить число 0, y 10 на р и записать целую часть m и дробную n часть произведения.
5) записать m в старший разряд дробной части р -ичного числа;
6) заменить число 0, y 10 на n.
Действия 4 – 6 повторить еще k –1 раз.
7) конец.
Пример 2. Перевести число 0,8110 в двоичную, восьмеричную и шестнадцатеричную системы счисления с точностью 0,006.
| Этап | Перевод в двоичную систему | Перевод в восьмеричную систему | Перевод в шестнадцатеричную систему | ||||||
| x 10 | m | n | x 10 | m | n | x 10 | m | n | |
| 
| 
| |||||||
| 0,81 | 0,62 | 0,81 | 0,48 | 0,81 | 0,96 | ||||
| 0,62 | 0,24 | 0,48 | 0,84 | 0,96 | 0,36 | ||||
| 0,24 | 0,48 | 0,84 | 0,72 | ||||||
| 0,48 | 0,96 | ||||||||
| 0,96 | 0,92 | ||||||||
| 0,92 | 0,84 | ||||||||
| 0,84 | 0,68 |
Т.о., 0,8110 = 0,110 01112 = 0,6368 = 0,CF16.
Если число является неправильной десятичной дробью, то есть содержит как целую, так и дробную части, к этим частям по отдельности применяются соответствующие алгоритмы преобразования. Тогда число 7 313,8110 будет представлено в двоичной, восьмеричной и шестнадцатеричной системах счисления с точностью 0,006 следующим образом:
7 313,8110 = 1 110 010 010 001,110 011 12 = 16 221,6368 = 1 C91,CF16.
Перевод р -ичного числа в десятичную систему счисления
Для перевода p -ичного числа в десятичную систему счисления используется формула (1), причем операции сложения, умножения и возведения в степень в этой формуле проводятся в десятичной системе.
Пример 3. Перевести двоичное число 1 110 010 010 001,11001112, восьмеричное 16 221,6368и шестнадцатеричное 1 C91,CF16в десятичную систему счисления.
1 110 010 010 001,11001112 = 1·212 + 1·211 + 1·210 + 1·27 + 1·24 + 1·20 + 1·2-1 + 1·2-2 + 1·2-5 + 1·2-6 + 1·2-7 =
= 4096 + 2048 + 1024 + 128 + 16 + 1 + 1/2 + 1/4 + 1/32 + 1/64 + 1/128 = 7 313,804687510,
16 221,6368 = 1·84 + 6·83 + 2·82 + 2·81 + 1·80 + 6·8-1 + 3·8-2 + 6·8-3 = 212 + 6·29 + 2·26 + 2·23 + 1 + 6/23 + 3/26 + 6/29 = = 4096 + 6·512 + 128 + 16 + 1 + 6/8 + 3/64 + 6/512 = 7 313,8085937510,
1 C91,CF16 = 1·163 + 12·162 + 9·161 + 1·160 + 2·16-1 + 15·16-2 = 212 + 12·256 + 9·16 + 1 + 12/16 + 15/256 =
= 4096 + 12·256 + 9·16 + 1 + 12/16 + 15/256 = 7 313,8085937510.
Проверим, что исходные двоичное, восьмеричное и шестнадцатеричное числа равны десятичному числу 7 313,8110 с точностью до ε = 0,006:
|7 313,8046875 – 7 313,81| = 0,0053125 < 0,006 = ε,
|7 313,80859375 – 7 313,81| = 0,00140625 < 0,006 = ε.
Преобразование между двоичной, восьмеричной и шестнадцатеричной системами счисления
Указанные системы счисления используются в компьютерах для представления информации. Основной системой является двоичная. В ней хранится абсолютно вся информация (числовая, текстовая, графическая, аудио- и видеоинформация). Для обозначения нуля и единицы используются электрические сигналы низкого и высокого уровня соответственно. При всем удобстве двоичной системы у нее есть существенный недостаток – запись в двоичной системе очень громоздкая (см. пример 1). Поэтому для сокращения двоичных чисел используются равные им восьмеричные или шестнадцатеричные числа.
Для преобразования между двоичной, восьмеричной и шестнадцатеричной системами счисления используются двоичные триады и двоичные тетрады (табл. 3).
Таблица 3
| Восьмеричный или шестнадцатеричный знак | Двоичная триада | Двоичная тетрада |
| – | ||
| – | ||
| A | – | |
| B | – | |
| C | – | |
| D | – | |
| E | – | |
| F | – |
Для того чтобы перевести восьмеричное (шестнадцатеричное) число в двоичную систему счисления, достаточно заменить каждую его цифру соответствующей двоичной триадой (тетрадой).
Пример 4. Перевести восьмеричное число 16221,6368 и шестнадцатеричное число 1C91,CF16 в двоичную систему счисления.
Решение. Переведем в двоичную систему счисления сначала исходное восьмеричное число.
1. Заменим в восьмеричном числе каждую цифру соответствующей двоичной триадой согласно табл. 3:
16221,6368 = 001 110 010 010 001,110 011 1102.
2. Удалим незначащие нули в полученном двоичном числе:
001 110 010 010 001,110 011 1102 = 1 110 010 010 001,110 011 112.
Аналогичным образом переведем заданное шестнадцатеричное число в двоичную систему счисления.
1. Заменим в шестнадцатеричном числе каждую цифру соответствующей двоичной тетрадой согласно табл. 3:
1C91,CF16 = 0001 1100 1001 0001,1100 11112.
2. Удалим незначащие нули в полученном двоичном числе:
0001 1100 1001 0001,1100 11112 = 1 1100 1001 0001,1100 11112.
Ответ. 16221,6368 = 1 110 010 010 001,110 011 112, 1C91,CF16 =1 1100 1001 0001,1100 11112.
Для того чтобы перевести двоичное число в восьмеричную (шестнадцатеричную) систему счисления, достаточно разбить его на двоичные триады (тетрады), а затем каждую из них заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
Пример 5. Перевести двоичное число 1110010010001,11001112 в восьмеричную и шестнадцатеричную системы счисления.
Решение. Переведем исходное число сначала в восьмеричную систему.
1. Разобьем разряды исходного двоичного числа на триады (по отдельности в целой и дробной частях):
1110010010001,11001112 = 1 110 010 010 001,110 011 12.
2. Мы видим, что после разбиения образовались две неполных триады (по одной в целой и в дробной частях). Чтобы двоичное число не изменилось, формально дополним эти триады нулями (в целой части – слева, в дробной – справа):
1 110 010 010 001,110 011 12 = 001 110 010 010 001,110 011 1002.
3. Заменим каждую двоичную триаду соответствующим восьмеричным знаком согласно табл. 3:
001 110 010 010 001,110 011 1002 = 16 221,6348.
Аналогичным образом переведем заданное число в шестнадцатеричную систему счисления.
1. Разобьем разряды исходного двоичного числа на тетрады:
1110010010001,11001112 = 1 1100 1001 0001,1100 1112.
2. Добавим в неполные тетрады нули:
1 1100 1001 0001,1100 1112 = 0001 1100 1001 0001,1100 11102.
3. Заменим каждую двоичную тетраду соответствующим восьмеричным знаком согласно табл. 3:
0001 1100 1001 0001,1100 11102 = 1 C91,CE16.
Ответ. 1110010010001,11001112 = 16 221,6348 = 1 C91,CE16.