Исторический очерк
Небесная механика принадлежит к числу древнейших наук. Уже в 6 век до н. э. народы Древнего Востока обладали глубокими астрономическими знаниями, связанными с движением небесных тел. Но в течение многих веков это была только эмпирическая кинематика Солнечной системы. Основы современной небесной механики были заложены Исааком Ньютоном в "Математических началах натуральной философии" (1687). Закон тяготения Ньютона далеко не сразу получил всеобщее признание. Однако уже к середине 18 века выяснилось, что он хорошо объясняет наиболее характерные особенности движения тел Солнечной системы (Ж. Д'Аламбер, А. Клеро). В работах Ж. Лагранжа и П. Лапласа были разработаны классические методы теории возмущений. Первая современная теория движения больших планет была построена У. Леверье в середине 19 в. Эта теория лежит до сих пор в основе французского национального астрономического ежегодника. В работах Леверье было впервые указано на необъяснимое законом Ньютона вековое смещение перигелия (самая близкая Солнцу точка орбиты) Меркурия, которое оказалось через 70 лет важнейшим наблюдательным подтверждением общей теории относительности.
Дальнейшее развитие теория больших планет получила в конце 19 веке в работах американских астрономов С. Нъюкома и Дж. Хилла (1895-98). Работы Нъюкома открыли новый этап в развитии небесной механики. Он впервые обработал ряды наблюдений, охватывающие длительные интервалы времени и на этой основе получил систему астрономических постоянных, которая только незначительно отличается от системы, принятой в 70-х годов 20 века. Чтобы согласовать теорию с наблюдаемым движением Меркурия, Ньюком решил прибегнуть к гипотезе А. Холла (1895), который для объяснения невязок в движении больших планет предложил изменить показатель степени в законе тяготения Ньютона. Ньюком принял показатель степени равным 2,00000016120. Закон Холла сохранялся в астрономических ежегодниках до 1960 г., когда он был, наконец, заменён релятивистскими поправками, вытекающими из общей теории относительности.
Продолжая традиции Ньюкома и Хилла, Бюро американских эфемерид (Вашингтонская морская обсерватория) под руководством Д. Брауэра и Дж. Клеменса в течение 40-х и 50-х годов 20 века осуществило обширные работы по переработке планетных теорий. В частности, в результате этой работы в 1951 были опубликованы "Координаты пяти внешних планет", что явилось важным шагом в исследовании орбит внешних планет.
Актуальное значение приобрела теория движения спутников больших планет, в первую очередь спутников Марса и Юпитера. Теория движения четырёх спутников Юпитера была разработана ещё Лапласом. В теории, предложенной В. Де’Ситтером (1919) и используемой в астрономических ежегодниках, учитываются сжатие Юпитера, солнечные возмущения и взаимные возмущения спутников. Внешние спутники Юпитера изучались в Институте теоретической астрономии АН СССР. Эфемериды (таблицы предвычисленных небесных координат Солнца, Луны, планет и других астрономических объектов на последовательные моменты времени, например, на полночь каждых суток) этих спутников до 2000 года вычислены американским астрономом П. Хергетом (1968) с помощью численного интегрирования. Теория движения спутников Сатурна, основанная на классических методах, была построена немецким астрономом Г. Струве (1924-33). Устойчивость спутниковых систем рассмотрена в работах японского астронома Ю. Хагихара (1952). Советский математик M. Л. Лидов, анализируя эволюцию орбит искусственных спутников планет, получил интересные результаты и для естественных спутников. Им было впервые показано (1961), что, если бы орбита Луны имела наклон к плоскости эклиптики (от лат. (linea) ecliptica, от греч. έκιειρσις — затмение), большой круг небесной сферы, по которому происходит видимое годичное движение Солнца, точнее — его центра.), равный 90°, то такая Луна уже после 55 оборотов, т. е. примерно через четыре года, упала на поверхность Земли.
Наряду с разработкой теории высокой степени точности, но пригодной только на сравнительно небольших интервалах времени (сотни лет), в небесной механики ведутся также исследования движения тел Солнечной системы в космогонических масштабах времени, т. е. на протяжении сотен тысяч и миллионов лет. Попытки решить эту проблему долгое время не давали удовлетворительных результатов. Только появление быстродействующих вычислит, машин, произведших революцию в небесной механике, позволило снова вернуться к решению этой фундаментальной задачи. В СССР и за рубежом разработаны эффективные методы построения аналитической теории движения больших планет, открывающие возможность изучения движения планет на весьма длительных промежутках времени.
Развитие небесной механики в СССР тесно связано с деятельностью двух научных центров, возникших непосредственно после Великой Октябрьской социалистической революции: Теоретической астрономии института АН СССР в Ленинграде и кафедры небесной механики Московского университета. В этих двух центрах сложились ленинградская и московская школы, которыерые определили развитие небесной механике в СССР. В Ленинграде вопросы небесной механики разрабатывались главным образом в связи с такими практическими задачами, как составление астрономических ежегодников, вычисление эфемерид малых планет и др. В Москве доминирующее влияние на протяжении многих лег имели космогонические проблемы, а также астродинамика.
Среди иностранных научных учреждений, ведущих исследования в области небесной мехенике видное место занимают: Вашингтонская морская обсерватория, Гринвичская астрономическая обсерватория, Бюро долгот в Париже, Астрономический институт в Гейдельберге и др.
Классической задачей небесной механики является задача об устойчивости Солнечной системы. Эта проблема тесно связана с существованием вековых изменений больших полуосей и наклонов планетных орбит. Методами небесной механики вопрос об устойчивости Солнечной системы не может быть полностью решён, так как математические ряды, используемые в задачах небесной механики, пригодны только для ограниченного интервала времени.
Самостоятельная работа №4
Тема: Фаза колебаний автоколебаний
Выполнила: студентка группы 1-РП
Шпак Елизавета
2016 Г.
Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.
В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.
Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω0.
Если свободные колебания происходят на частоте ω0, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы.
После начала воздействия внешней силы на колебательную систему необходимо некоторое время Δ t для установления вынужденных колебаний. Время установления по порядку величины равно времени затухания τ свободных колебаний в колебательной системе.
В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте ω и свободные колебания на собственной частоте ω0. Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте ω внешней вынуждающей силы.
Рассмотрим в качестве примера вынужденные колебания тела на пружине (рис. 2.5.1). Внешняя сила 
приложена к свободному концу пружины. Она заставляет свободный (левый на рис. 2.5.1) конец пружины перемещаться по закону
| y = y m cos ω t. |
где y m – амплитуда колебаний, ω – круговая частота.
Такой закон перемещения можно обеспечить с помощью шатунного механизма, преобразующего движение по окружности в поступательно-возвратное движение
| Вынужденные колебания груза на пружине. Свободный конец пружины перемещается по закону y = y m cos ω t. l – длина недеформированной пружины, k – жесткость пружины |
Если левый конец пружины смещен на расстояние y, а правый – на расстояние x от их первоначального положения, когда пружина была недеформирована, то удлинение пружины Δ l равно:
| Δ l = x – y = x – y m cos ω t. |
Второй закон Ньютона для тела массой m принимает вид:
| ma = – k (x – y) = – kx + ky m cos ω t. |
В этом уравнении сила, действующая на тело, представлена в виде двух слагаемых. Первое слагаемое в правой части – это упругая сила, стремящаяся возвратить тело в положение равновесия (x = 0). Второе слагаемое – внешнее периодическое воздействие на тело. Это слагаемое и называют вынуждающей силой.
Уравнению, выражающему второй закон Ньютона для тела на пружине при наличии внешнего периодического воздействия, можно придать строгую математическую форму, если учесть связь между ускорением тела и его координатой: 
Тогда уравнение вынужденных колебаний запишется в виде
| (**) |
где 
– собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина A определяется выражением:
|
Уравнение (**) не учитывает действия сил трения. В отличие от уравнения свободных колебаний (*) (см. §2.2) уравнение вынужденных колебаний (**) содержит две частоты – частоту ω0 свободных колебаний и частоту ω вынуждающей силы.
Установившиеся вынужденные колебания груза на пружине происходят на частоте внешнего воздействия по закону
|
Примером механической автоколебательной системы может служить часовой механизм с анкерным ходом (рис. 2.5.4). Ходовое колесо с косыми зубьями жестко скреплено с зубчатым барабаном, через который перекинута цепочка с гирей. На верхнем конце маятника закреплен анкер (якорек) с двумя пластинками из твердого материала, изогнутыми по дуге окружности с центром на оси маятника. В ручных часах гиря заменена пружиной, а маятник – балансиром – маховичком, скрепленным со спиральной пружиной. Балансир совершает крутильные колебания вокруг своей оси. Колебательной системой в часах является маятник или балансир. Источником энергии – поднятая вверх гиря или заведенная пружина. Устройством, с помощью которого осуществляется обратная связь, является анкер, позволяющий ходовому колесу повернуться на один зубец за один полупериод. Обратная связь осуществляется взаимодействием анкера с ходовым колесом. При каждом колебании маятника зубец ходового колеса толкает анкерную вилку в направлении движения маятника, передавая ему некоторую порцию энергии, которая компенсирует потери энергии на трение. Таким образом, потенциальная энергия гири (или закрученной пружины) постепенно, отдельными порциями передается маятнику.
Механические автоколебательные системы широко распространены в окружающей нас жизни и в технике. Автоколебания совершают паровые машины, двигатели внутреннего сгорания, электрические звонки, струны смычковых музыкальных инструментов, воздушные столбы в трубах духовых инструментов, голосовые связки при разговоре или пении и т. д.
Самостоятельная работа № 6
Тема: Границы применимости модели идеального газа
Выполнила: Шпак Елизавета
Группа: 1-РП
2016 Г.
Идеальный газ – это модель разреженного газа, в которой пренебрегается взаимодействием между молекулами. Силы взаимодействия между молекулами довольно сложны. На очень малых расстояниях, когда молекулы вплотную подлетают друг к другу, между ними действуют большие по величине силы отталкивания. На больших или промежуточных расстояниях между молекулами действуют сравнительно слабые силы притяжения. Если расстояния между молекулами в среднем велики, что наблюдается в достаточно разреженном газе, то взаимодействие проявляется в виде относительно редких соударений молекул друг с другом, когда они подлетают вплотную. В идеальном газе взаимодействием молекул вообще пренебрегают.
Границы применимости модели идеального газа зависят от рассматриваемой задачи. Если необходимо установить связь между давлением, объемом и температурой, то газ с хорошей точностью можно считать идеальным до давлений в несколько десятков атмосфер. Если изучается фазовый переход типа испарения или конденсации или рассматривается процесс установления равновесия в газе, то модель идеального газа нельзя применять даже при давлениях в несколько миллиметров ртутного столба.
Давление газа на стенку сосуда является следствием хаотических ударов молекул о стенку, вследствие их большой частоты действие этих ударов воспринимается нашими органами чувств или приборами как непрерывная сила, действующая на стенку сосуда и создающая давление.
Пусть одна молекула находится в сосуде, имеющем форму прямоугольного параллелепипеда (рис. 1). Рассмотрим, например, удары этой молекулы о правую стенку сосуда, перпендикулярную оси Х. Считаем удары молекулы о стенки абсолютно упругими, тогда угол отражения молекулы от стенки равен углу падения, а величина скорости в результате удара не изменяется. В нашем случае при ударе проекция скорости молекулы на ось У не изменяется, а проекция скорости на ось Х меняет знак. Таким образом, проекция импульса изменяется при ударе на величину, равную 
, знак «-» означает, что проекция конечной скорости отрицательна, а проекция начальной – положительна.
Определим число ударов молекулы о данную стенку за 1 секунду. Величина проекции скорости не изменяется при ударе о любую стенку, т.е. можно сказать, что движение молекулы вдоль оси Х равномерное. За 1 секунду она пролетает расстояние, равное проекции скорости 
. От удара до следующего удара об эту же стенку молекула пролетает вдоль оси Х расстояние, равное удвоенной длине сосуда 2L. Поэтому число ударов молекулы о выбранную стенку равно 
. Согласно 2-му закону Ньютона средняя сила равна изменению импульса тела за единицу времени. Если при каждом ударе о стенку частица изменяет импульс на величину 
, а число ударов за единицу времени равно , то средняя сила, действующая со стороны стенки на молекулу (равная по величине силе, действующей на стенку со стороны молекулы), равна 
, а среднее давление молекулы на стенку равно 
, где V – объем сосуда.
Если бы все молекулы имели одинаковую скорость, то общее давление получалось бы просто умножением этой величины на число частиц N, т.е. 
. Но поскольку молекулы газа имеют разные скорости, то в этой формуле будет стоять среднее значение квадрата скорости, тогда формула примет вид: 
.
Квадрат модуля скорости равен сумме квадратов ее проекций, это имеет место и для их средних значений: 
. Вследствие хаотичности теплового движения средние значения всех квадратов проекций скорости одинаковы, т.к. нет преимущественного движения молекул в каком-либо направлении. Поэтому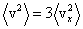 
, и тогда формула для давления газа примет вид: 
. Если ввести кинетическую энергию молекулы 
, то получим 
, где 
- средняя кинетическая энергия молекулы.
Согласно Больцману средняя кинетическая энергия молекулы пропорциональна абсолютной температуре 
, и тогда давление идеального газа равно 
или
. (1)
Если ввести концентрацию частиц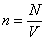 
, то формула перепишется так:
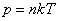. (2)
Число частиц можно представить в виде произведения числа молей на число частиц в моле, равное числу Авогадро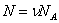 
, а произведение 
. Тогда (1) запишется в виде:
. (3)
Уравнения (1), (2) и (3) – это разные формы записи уравнения состояния идеального газа, они связывают давление, объем и температуру газа. Эти уравнения применимы как к чистым газам, так и к смесям газов, в последнем случае под N, n и ν следует понимать полное число молекул всех сортов, суммарную концентрацию или полное число молей в смеси. Для чистого газа число молей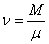 
, где М – масса газа, а μ – масса одного моля (молярная масса). Тогда уравнение (3) примет вид:
. (4)
Уравнение состояния в этой форме называют уравнением Клапейрона–Менделеева.
Рассмотрим частные газовые законы. При постоянной температуре и массе из (4) следует, что 
, т.е. при постоянной температуре и массе газа его давление обратно пропорционально объему. Этот закон называется законом Бойля и Мариотта, а процесс, при котором температура постоянна, называется изотермическим.
Для изобарного процесса, происходящего при постоянном давлении, из (4) следует, что 
, т.е. объем пропорционален абсолютной температуре. Этот закон называют законом Гей-Люссака.
Для изохорного процесса, происходящего при постоянном объеме, из (4) следует, что 
, т.е. давление пропорционально абсолютной температуре. Этот закон называют законом Шарля.
Эти три газовых закона, таким образом, являются частными случаями уравнения состояния идеального газа. Исторически они сначала были открыты экспериментально, и лишь значительно позднее получены теоретически, исходя из молекулярных представлений.
Самостоятельная работа № 5
Тема: Уравнение гармонической волны
Выполнила: Шпак Елизавета
Группа: 1-РП
2016 Г.
Уравнениям (8) удовлетворяют, в частности, плоские электромагнитные гармонические волны, описываемые уравнениями
(9)
где Е 0, Н 0 – амплитуды напряженностей электрического и магнитного полей; w= 2 p/Т= 2 pn – круговая частота (с- 1); Т – период колебаний (с); n= 1 /Т – частота колебаний (Гц); k=w/v= 2 p/l – волновое число; v – скорость распространения волны, для нее скорость переноса энергии (групповая скорость) u равна фазовой скорости v этой волны [см.(1.14)]; l= v T – длина волны, для вакуума
l=сT=с/ n, (10)
j 0 – начальные фазы колебаний в точках с координатой x = 0.
В уравнениях гармонической волны (9) j 0 – одинаково, т.к. колебания электрического и магнитного векторов в электромагнитной волне происходят в одинаковой фазе [это следует из (1)].
На рис.2. показаны векторы 
и 
поля плоской линейно поляризованной волны в различных точках луча (оси ох) в один и тот же момент времени. Плоскость, проходящая через электрический вектор и луч (или вектор 
), называется плоскостью поляризации.
Электромагнитную гармоническую волну часто записывают в экспоненциальной (комплексной) форме аналогично (1.6), где вместо s и А 0 будет Е и Е 0, Н и Н 0соответственно для электрического и магнитного векторов.
Электромагнитная волна так же, как упругая волна (см. параграф 1.3) характеризуется фронтом волны, волновой поверхностью. В отличие от упругих волн, которые распространяются только в среде (в вакууме упругие волны не могут распространяться, т.к. в нем нет частиц, которые совершали бы колебания), электромагнитные волны распространяются не только в среде, но и в вакууме, т.к. они представляют собой процесс распространения колебаний векторов и в пространстве.
Как и в случае упругих волн по форме волновых поверхностей или волновому фронту различают плоские, сферические, цилиндрические и прочие электромагнитные волны.
Обычно в практике используются пучки электромагнитной энергии (света) конечного поперечного сечения. Конечный, но достаточно узкий пучок будем называть лучом. Луч всегда перпендикулярен волновому фронту.
Из уравнений Максвелла (1) следует, что электромагнитные волны являются поперечными волнами, т.к. векторы и колеблются перпендикулярно к направлению распространения волны (см. рис. 1 и 2).
Самостоятельная работа № 7
По физике
Тема: Поверхностное натяжение
Выполнила: студентка группы 1-РП
Шпак Елизавета
Свойства жидкостей. Поверхностное натяжение
Молекулы вещества в жидком состоянии расположены почти вплотную друг к другу. В отличие от твердых кристаллических тел, в которых молекулы образуют упорядоченные структуры во всем объеме кристалла и могут совершать тепловые колебания около фиксированных центров, молекулы жидкости обладают большей свободой. Каждая молекула жидкости, также как и в твердом теле, «зажата» со всех сторон соседними молекулами и совершает тепловые колебания около некоторого положения равновесия. Однако, время от времени любая молекула может переместиться в соседнее вакантное место. Такие перескоки в жидкостях происходят довольно часто; поэтому молекулы не привязаны к определенным центрам, как в кристаллах (см. §3.6), и могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей. Из-за сильного взаимодействия между близко расположенными молекулами они могут образовывать локальные (неустойчивые) упорядоченные группы, содержащие несколько молекул. Это явление называется ближним порядком (рис. 3.5.1).
|
| Рисунок 3.5.1. Пример ближнего порядка молекул жидкости и дальнего порядка молекул кристаллического вещества: 1 – вода; 2 – лед |
Рис. 3.5.2 иллюстрирует отличие газообразного вещества от жидкости на примере воды. Молекула воды H2O состоит из одного атома кислорода и двух атомов водорода, расположенных под углом 104°. Среднее расстояние между молекулами пара в десятки раз превышает среднее расстояние между молекулами воды. В отличие от рис. 3.5.1, где молекулы воды изображены в виде шариков, рис. 3.5.2 дает представление о структуре молекулы воды.
|
| Рисунок 3.5.2. Водяной пар (1) и вода (2). Молекулы воды увеличены примерно в 5·107 раз |
Вследствие плотной упаковки молекул сжимаемость жидкостей, т. е. изменение объема при изменении давления, очень мала; она в десятки и сотни тысяч раз меньше, чем в газах. Например, для изменения объема воды на 1 % нужно увеличить давление приблизительно в 200 раз. Такое увеличение давления по сравнению с атмосферным достигается на глубине около 2 км.
Жидкости, как и твердые тела, изменяют свой объем при изменении температуры. Для не очень больших интервалов температур относительное изменение объема Δ V / V 0пропорционально изменению температуры Δ T:
|
Коэффициент β называют температурным коэффициентом объемного расширения. Этот коэффициент у жидкостей в десятки раз больше, чем у твердых тел. У воды, например, при температуре 20 °С βв ≈ 2·10–4 К–1, у стали βст ≈ 3,6·10–5 К–1, у кварцевого стекла βкв ≈ 9·10–6 К–1.
Тепловое расширение воды имеет интересную и важную для жизни на Земле аномалию. При температуре ниже 4 °С вода расширяется при понижении температуры (β < 0). Максимум плотности ρв = 103 кг/м3 вода имеет при температуре 4 °С.
При замерзании вода расширяется, поэтому лед остается плавать на поверхности замерзающего водоема. Температура замерзающей воды подо льдом равна 0 °С. В более плотных слоях воды у дна водоема температура оказывается порядка 4 °С. Благодаря этому жизнь может существовать в воде замерзающих водоемов.
Наиболее интересной особенностью жидкостей является наличие свободной поверхности. Жидкость, в отличие от газов, не заполняет весь объем сосуда, в который она налита. Между жидкостью и газом (или паром) образуется граница раздела, которая находится в особых условиях по сравнению с остальной массой жидкости. Молекулы в пограничном слое жидкости, в отличие от молекул в ее глубине, окружены другими молекулами той же жидкости не со всех сторон. Силы межмолекулярного взаимодействия, действующие на одну из молекул внутри жидкости со стороны соседних молекул, в среднем взаимно скомпенсированы. Любая молекула в пограничном слое притягивается молекулами, находящимися внутри жидкости (силами, действующими на данную молекулу жидкости со стороны молекул газа (или пара) можно пренебречь). В результате появляется некоторая равнодействующая сила, направленная вглубь жидкости. Поверхностные молекулы силами межмолекулярного притяжения втягиваются внутрь жидкости. Но все молекулы, в том числе и молекулы пограничного слоя, должны находиться в состоянии равновесия. Это равновесие достигается за счет некоторого уменьшения расстояния между молекулами поверхностного слоя и их ближайшими соседями внутри жидкости. Как видно из рис. 3.1.2, при уменьшении расстояния между молекулами возникают силы отталкивания. Если среднее расстояние между молекулами внутри жидкости равно r 0, то молекулы поверхностного слоя упакованы несколько более плотно, а поэтому они обладают дополнительным запасом потенциальной энергии по сравнению с внутренними молекулами (см. рис. 3.1.2). Следует иметь ввиду, что вследствие крайне низкой сжимаемости наличие более плотно упакованного поверхностного слоя не приводит к сколь-нибудь заметному изменению объема жидкости. Если молекула переместится с поверхности внутрь жидкости, силы межмолекулярного взаимодействия совершат положительную работу. Наоборот, чтобы вытащить некоторое количество молекул из глубины жидкости на поверхность (т. е. увеличить площадь поверхности жидкости), внешние силы должны совершить положительную работу Δ A внеш, пропорциональную изменению Δ S площади поверхности:
| Δ A внеш = σΔ S. |
Коэффициент σ называется коэффициентом поверхностного натяжения (σ > 0). Таким образом, коэффициент поверхностного натяжения равен работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу.
В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м2) или в ньютонах на метр (1 Н/м = 1 Дж/м2).
Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Потенциальная энергия E р поверхности жидкости пропорциональна ее площади:
|
Из механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии. Отсюда следует, что свободная поверхность жидкости стремится сократить свою площадь. По этой причине свободная капля жидкости принимает шарообразную форму. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, сокращающие (стягивающие) эту поверхность. Эти силы называются силами поверхностного натяжения.
Наличие сил поверхностного натяжения делает поверхность жидкости похожей на упругую растянутую пленку, с той только разницей, что упругие силы в пленке зависят от площади ее поверхности (т. е. от того, как пленка деформирована), а силы поверхностного натяжения не зависят от площади поверхности жидкости.
Некоторые жидкости, как, например, мыльная вода, обладают способностью образовывать тонкие пленки. Всем хорошо известные мыльные пузыри имеют правильную сферическую форму – в этом тоже проявляется действие сил поверхностного натяжения. Если в мыльный раствор опустить проволочную рамку, одна из сторон которой подвижна, то вся она затянется пленкой жидкости (рис. 3.5.3).
|
Рисунок 3.5.3.
Подвижная сторона проволочной рамкив равновесии под действием внешней силы  и результирующей сил поверхностного натяжения 
|
Силы поверхностного натяжения стремятся сократить поверхность пленки. Для равновесия подвижной стороны рамки к ней нужно приложить внешнюю силу 
Если под действием силы перекладина переместится на Δ x, то будет произведена работа Δ A вн = F внΔ x = Δ Ep = σΔ S, где Δ S = 2 L Δ x – приращение площади поверхности обеих сторон мыльной пленки. Так как модули сил и одинаковы, можно записать:
|
Таким образом, коэффициент поверхностного натяжения σ может быть определен как модуль силы поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность.
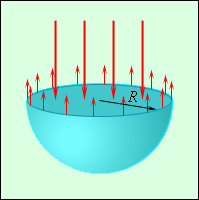
Из-за действия сил поверхностного натяжения в каплях жидкости и внутри мыльных пузырей возникает избыточное давление Δ p. Если мысленно разрезать сферическую каплю радиуса R на две половинки, то каждая из них должна находиться в равновесии под действием сил поверхностного натяжения, приложенных к границе разреза длиной 2π R и сил избыточного давления, действующих на площадь π R 2 сечения (рис. 3.5.4). Условие равновесия записывается в виде
| σ2π R = Δ p π R 2. |
Отсюда избыточное давление внутри капли равно
|
(капля жидкости).
|
| Рисунок 3.5.4. Сечение сферической капли жидкости |
Избыточное давление внутри мыльного пузыря в два раза больше, так как пленка имеет две поверхности:
|
(мыльный пузырь).
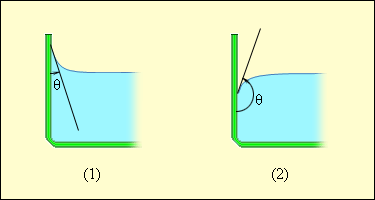
Вблизи границы между жидкостью, твердым телом и газом форма свободной поверхности жидкости зависит от сил взаимодействия молекул жидкости с молекулами твердого тела (взаимодействием с молекулами газа (или пара) можно пренебречь). Если эти силы больше сил взаимодействия между молекулами самой жидкости, то жидкость смачивает поверхность твердого тела. В этом случае жидкость подходит к поверхности твердого тела под некоторым острым углом θ, характерным для данной пары жидкость – твердое тело. Угол θ называется краевым углом. Если силы взаимодействия между молекулами жидкости превосходят силы их взаимодействия с молекулами твердого тела, то краевой угол θ оказывается тупым (рис. 3.5.5). В этом случае говорят, что жидкость не смачивает поверхность твердого тела. При полном смачивании θ = 0, при полном несмачивании θ = 180°.
|
| Рисунок 3.5.5. Краевые углы смачивающей (1) и несмачивающей (2) жидкостей |
Капиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются.
На рис. 3.5.6 изображена капиллярная трубка некоторого радиуса r, опущенная нижним концом в смачивающую жидкость плотности ρ. Верхний конец капилляра открыт. Подъем жидкости в капилляре продолжается до тех пор, пока сила тяжести 
действующая на столб жидкости в капилляре, не станет равной по модулю результирующей F нсил поверхностного натяжения, действующих вдоль границы соприкосновения жидкости с поверхностью капилляра: F т = F н, где F т = mg = ρ h π r 2 g, F н = σ2π r cos θ.
Отсюда следует:
|
|
| Рисунок 3.5.6. Подъем смачивающей жидкости в капилляре |
При полном смачивании θ = 0, cos θ = 1. В этом случае
|
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
Вода практически полностью смачивает чистую поверхность стекла. Наоборот, ртуть полностью не смачивает стеклянную поверхность. Поэтому уровень ртути в стеклянном капилляре опускается ниже уровня в сосуде.
Самостоятельная работа №3
По физике
Тема: Механические свойства твердых тел
Выполнила: студентка группы 1-РП
Шпак Елизавета
| ||||||||
Под действием сил форма твердых тел меняется, происходит их деформация (от латинского deformatio – искажение). При деформациях может меняться и объем тел.
|
