Тема: «Применение производной к исследованию функций»
Промежутки возрастания и убывания функции
· Функция называется возрастающей на данном промежутке, если большему значению аргумента соответствует большее значение функции.
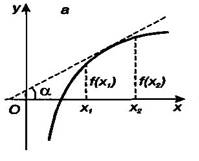 f(x2) > f(x1) при x2 > x1
f(x2) > f(x1) при x2 > x1
· Функция называется убывающей на данном промежутке, если большему значению аргумента соответствует меньшее значение функции.
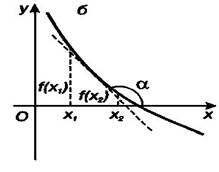 f(x2) < f(x1) при x2 > x1
f(x2) < f(x1) при x2 > x1
Признак возрастания: Если функция определена, дифференцируема и возрастает на некотором промежутке, то ее производная положительна в каждой точке этого промежутка.
f ′(x)>0
Признак убывания: Если функция определена, дифференцируема и убывает на некотором промежутке, то ее производная отрицательна в каждой точке этого промежутка.
f ′(x)<0
· Точки, в которых производная равна нулю или не существует, называются критическими точками.
Пример:
Исследуйте функцию y=2x3-15x2+36x-14 на монотонность.
Решение: 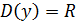
y’=6x2-30x+36
6x2-30x+36=0
x2-5x+6=0
x1=2 x2=3, критические точки.
Определяем знак производной на каждом интервале.
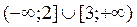

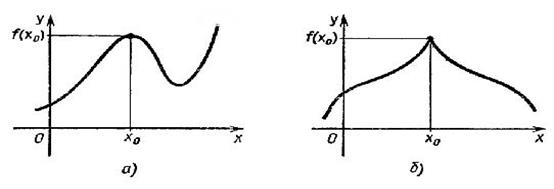
Ответ: функция возрастает при хЄ
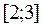 функция убывает при хЄ
функция убывает при хЄ
Экстремумы функции
· Точка x0 из области определения функции называется точкой минимума, если для всех х из некоторой окрестности точки x0 выполняется условие f(x0)<f(x).
· Точка x0 из области определения функции называется точкой максимума, если для всех х из некоторой окрестности точки x0 выполняется условие f(x0)>f(x).
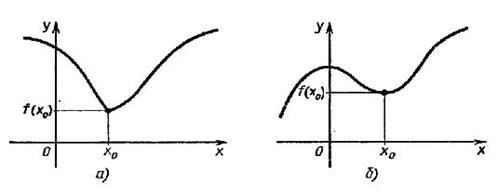
Признаки максимума и минимума функции:
Если f ′(x0)=0 и при переходе через точку x0 производная f ′(x)меняет знак с + на -, то в точке x0 - максимум;
если же производная f ′(x) меняет знак с – на +, то в точке x0 - минимум.
Пример: Исследовать функцию y=x3-9x2+24x-12 на максимум и минимум.
Решение: 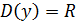
y’=3x2-18x+24
3x2-18x+24=0
x1=4 x2=2, критические точки.
Определяем знак производной на каждом интервале.
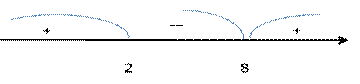
Xmax=2 Xmin=4
ymax =y(2)= 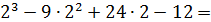 8
8
ymin =y(4)= 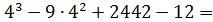 4
4
Ответ: (2;8)-точка max
(4;4)-точка min
Промежутки выпуклости графика. Точки перегиба.
· График функции называется выпуклым вниз, если он расположен выше касательной, проведенной к графику функции (рис. а); в противном случае график функции называется выпуклым вверх (рис.б).
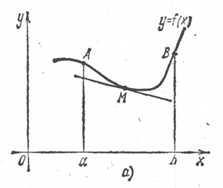
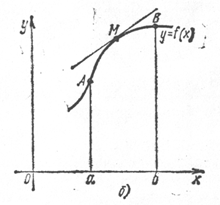
Признак выпуклости вверх: Если функция определена, дифференцируема и выпукла вверх на некотором промежутке, то ее вторая производная отрицательна в каждой точке этого промежутка.
f ′’(x)<0
Признак выпуклости вниз: Если функция определена, дифференцируема и выпукла вниз на некотором промежутке, то ее вторая производная положительна в каждой точке этого промежутка.
f ′’(x)>0
· Точки, в которых вторая производная равна нулю или не определена, называются критическими точками II рода.
· Точки, в которых график функции меняет направление выпуклости, называются точками перегиба.

Признак точки перегиба: Если в точке x0 вторая производная 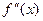 обращается в нуль или терпит разрыв, и при переходе через критическую точку x0 вторая производная
обращается в нуль или терпит разрыв, и при переходе через критическую точку x0 вторая производная 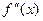 меняет знак, то график функции
меняет знак, то график функции 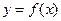 имеет точку перегиба (x0; f(x0 )).
имеет точку перегиба (x0; f(x0 )).
Пример: Найти интервалы выпуклости функции и точки перегиба y=1/10x5-5/6x3+2x.
Решение:
y’=x4/2-5x2/2+2
y’’=2x3-5x
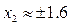 y’’=x(2x2-5)
y’’=x(2x2-5)
x1=0 или, критические точки второго рода.
Определяем знак второй производной на каждом промежутке.

x1=0 y1=0
x2=-1.6 y2=-0.9
x3=1.6 y3=0.9
Ответ: на промежутках (-¥;-1,6]È[0;1,6) – функция выпукла вверх, на промежутках [-1,6;0]È[1,6;+¥) – функция выпукла вниз,
точки перегиба (-1,6;-0,9), (0;0), (1,6;0,9).
План исследования функции:
1. Найдите область определения функции.
2. Исследуйте функцию на четность.
3. Найдите первую производную и критические точки.
4. Определите промежутки монотонности и найдите точки экстремума.
5. Найдите вторую производную и критические точки.
6. Определите направления выпуклости графика функции и найдите точки перегиба.
7. Найдите асимптоты графика.
8. Найдите точки пересечения графика функции с осями координат.
9. Постройте график.
Пример: Исследуйте функцию и постройте график функции 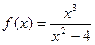 .
.
1. 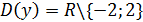 ; D(f) симметричная относительно 0.
; D(f) симметричная относительно 0.
2. Функция нечетная, т.к. 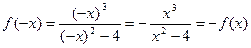 график симметричен относительно начала координат.
график симметричен относительно начала координат.
3. 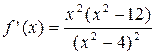 ,
, 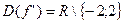
Критические точки I рода:  ,
, 
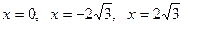
х=2 и х=-2 также являются критическими точками, т.к. 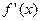 не осуществляет в этих точках, но эти точки не входят в область определения функции, поэтому должны быть исключены из рассмотрения.
не осуществляет в этих точках, но эти точки не входят в область определения функции, поэтому должны быть исключены из рассмотрения.
3.

 .
.
Функция возрастает  и
и 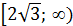 , убывает
, убывает 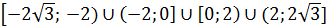 .
.
5.  . Критические точки II рода:
. Критические точки II рода: 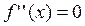
 , х=о.
, х=о.
х=2 и х=-2 также являются критическими точками, т.к.  не осуществляет в этих точках.
не осуществляет в этих точках.
6.
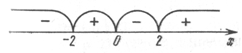
Функция выпукла вверх  , выпукла вниз
, выпукла вниз 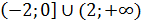 ,
,
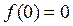 (0; 0) – точка перегиба.
(0; 0) – точка перегиба.
7. Асимптоты графика:
а). 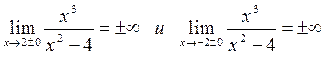 значит, х=-2 и х=2 – вертикальные асимптоты.
значит, х=-2 и х=2 – вертикальные асимптоты.
б).. 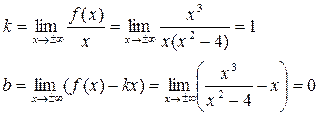
Значит, у=х – наклонная асимптота.
