Назначение МАТЛАБа: предназначен для выполнения вычислений, таких как
· Простейшие расчеты по формулам;
· Решение нелинейных уравнений и систем;
· Решение задач линейной алгебры;
· Решение задач оптимизации;
· Дифференцирование и интегрирование;
· Задачи обработки экспериментальных данных (интерполяция, аппроксимация, метод наименьших квадратов);
· Решение обыкновенных дифференциальных уравнений и систем;
· Решение дифференциальных уравнений в частных производных;
Кроме того МАТЛАБ предоставляет широкие возможности по созданию графиков (плоских и объемных).
МАТЛАБ позволяет снабдить его программы визуальным интерфейсом.
Интерфейс: после запуска появляется основное окно приложения
Оно содержит меню, панель инструментов, рабочую область Command Window, список последних команд в окне Command History, список файлов в рабочей папке в окне Current Directory, которое может быть заменено на окно Workspace содержащее список переменных, их тип и значение в текущий момент.
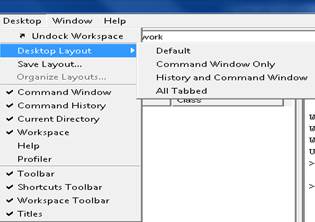Команда меню Desktop позволяет выбрать размещение окон
Desktop Layout предлагает Default по умолчанию тот набор окон, который уже продемонстрирован, а также другие варианты.
Операции в CommandWindow: курсор расположен после знака >> содержащую курсор строку называют командной строкой.
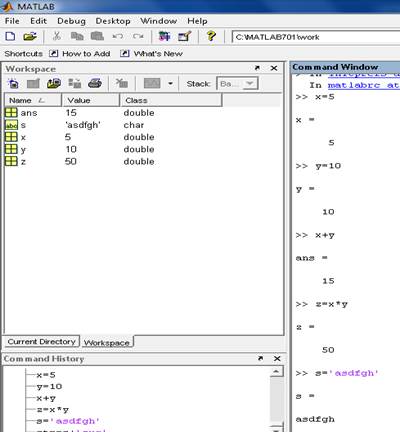По мере работы текст в окне смещается вверх за пределы окна. Но он сохраняется. Можно снова получить в командной строке вышележащую (нижележащую) строку с текстом, пользуясь стрелками вверх (вниз).
Область текста выше командной строки доступна только для копирования.
При вводе команды заканчиваются точкой с запятой; иначе сразу же произойдет вывод на экран результатов выполнения.
|
|
Если не предусмотрено имя переменной для результата вычисления то по умолчанию присваивается имя ans
Текущий документ, отражающий работу пользователя и содержащий строки ввода, вывода и сообщения об ошибках, принято называть сессией. Значения переменных, вычисленные в течение сессии, сохраняются в области памяти Workspace. Определения всех переменных и функций данной сессии можно сохранить в файл с расширением.mat но саму сессию сохранить нельзя.
УПРАЖНЕНИЯ. Элементарные операции в CommandWindow.
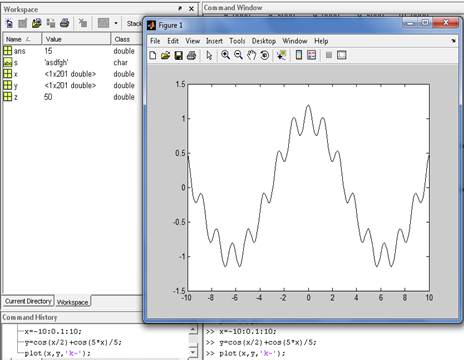
Построим график функции одной переменной. Для этого зададим диапазон значений переменной х аргумента функции. Пусть х массив чисел, его первый элемент равен -10, его последний элемент равен 10, шаг 0.1 (то есть каждый следующий элемент больше предыдущего на 0.1). для этого введем командной строке команду
x=-10:0.1:10; Затем получим значения функции у(х). Для этого в командной строке введем команду y=cos(x/2)+cos(5*x)/5; В окне Workspace после этого будут видны сведения о том что х и у являются массивами чисел и состоят из 201 элемента каждый. Важно что количество элементов в двух массивах совпадает. Тогда при построении графика число из одного массива будет горизонтальной координатой точки, а число из другого массива будет вертикальной координатой точки. Таким образом график построится. Команда на построение графика plot(x,y,’k-‘); где сначала указан массив координат по горизонтальной оси, затем по вертикальной, а затем указание о цвете линии (k означает черный цвет) и типе маркеров (‘k-‘ означает черную линию без маркеров). Все эти команды видны в окне Command History где они сохраняются.
|
|
Построим несколько графиков одновременно.
Для этого зададим массив х от -6,28 с шагом 0,1 до 6,28. x=-6.28:0.1:6.28; Затем зададим функции y(x), z(x), v(x). y=sin(x/2); z=cos(x); v=exp(cos(x)); После этого введем в командной строке команду plot(x,y,'k-',x,z,'r.',x,v,'o-'); где каждой паре (горизонтальные координаты, вертикальные координаты) указан тип маркера и цвет линии. (‘r.’ красные точки без линии, ‘o-‘ синие кружочки с линией).
Кроме того, команда grid on наносит сетку на график, функция title(‘Заголовок’) выводит заголовок графика, функции xlabel(‘Подпись под осью Х’), ylabel(‘Подпись под осью У’) служат для подписи осей.
Построим несколько графиков отдельно друг от друга, но в одном окне.
Команда subplot(3,2,1); означает что окно разбивается на три маленьких окна для построения графиков по вертикали, на две колонки таких окон по горизонтали, и начинаем описывать первый (левый верхний) из графиков. Аналогично последующие команды subplot отличаются только номером очередного графика.
При описании функций, содержащих операции умножения и возведения в степень, надо учитывать, что их аргумент является массивом чисел. Соответственно, функция тоже будет получена в виде массива. Его элементы будут результатом поэлементного обращения функции к массиву аргумента. Поэтому ставится знак «точка» при описании функции y=cos(t).^2; или u=sin(t).^2; знак «точка» ставится после аргумента, перед знаком операции возведения в степень.
Текст (последовательность команд) виден в окне Command Window. Его нижняя часть не поместилась, поэтому в окне Command History она видна как продолжение текста показанного в Command Window, начиная с команды plot(t,v,'c-');
|
|
Построим график в полярной системе координат. Для этого сформируем массив значений полярного угла phi и полярного радиуса ro и используем команду polar(phi, ro, s), где s строка из трех символов, задающих цвет линии, тип маркера и тип линии. Можно ограничиться только цветом и типом линии. В МАТЛАБе предусмотрена автозамена комбинаций латинских букв на греческие буквы. Так например \phi заменяется на ϕ, \rho заменяется на ρ. Поэтому в команде title(‘Заголовок’) указываем в заголовке не греческие буквы а соответствующие им комбинации латинских букв.
Построим график функции, заданной в параметрической форме. Для этого определим массив параметра t. Затем определим массивы функций от параметра. Пусть x=f(t), y=g(t). Затем построим график функции у(х) с помощью команды plot(x,y).
Построим график a2x3-y2=0 (a>0). Параметрическое представление таково: x=t2, y=at3, -∞<t<∞. Пусть а=3.
Рядом построим график (x+a)a2+(x-a)y2=0, a>0. Параметрическое представление таково: x(t)=a(t2-1)/(t2+1), y(t)=at(t2-1)/(t2+1)
В МАТЛАБе графики можно модифицировать, используя возможности графического окна, в котором они отображаются. Для этого с помощью инструмента «стрелка» выделяется элемент, а затем щелчками кнопок мыши открываются соответствующие списки действий или пункты меню.
Команда File-Generate M-file позволяет автоматически сгенерировать файл с программой, строящей именно такой график.
Ее можно сохранить, нажав на сохранение.
Построим трехмерный график z(x,y). Для этого необходимо по каждой из двух переменных x и y создать массив двумерный. Например x=-2:2 и y=-3: 3. Массивы создаются командой
[x y]=meshgrid(-2:2, -3:3) таким образом сформировали сетку координат по х и по у.
Затем вычислим для каждой точки с координатами (х,у) значение функции z(x,y) то есть координаты этих точек по оси z.
z=y.^2-x.^2 После формирования массива координат по оси z обратимся к функции mesh(x,y,z), которая по имеющимся координатам построит поверхность.
Кроме того, есть еще функция для построения поверхности, покрашенной в соответствии со значениями z(x,y) то есть чем-то похоже на географическую карту с окраской по высоте изображенных участков местности. Для нее тоже строим сетку функцией meshgrid, затем находим значения (массив значений) z(x,y) и тогда уже вызываем surf(x,y,z).
Трехмерную фигуру можно повернуть любой стороной и рассмотреть поудобней. Для этого в окне фигуры надо ткнуть кнопку Rotate3D и можно мышкой зацепить и повертеть фигуру.
Если надо построить две трехмерные фигуры в одном окне то используется команда hold on которая вынуждает МАТЛАБ построить новую трехмерную поверхность в прежнем окне.
Построим поверхность заданную параметрически.
х(u,v)=ch(u)cos(v), y(u,v)=ch(u)sin(v), z(u,v)=sh(u).
Построим сначала для параметра u вектор-столбец u=(0:3.14/50:3.14)’; знак ‘ означает транспонирование.
Затем для второго параметра v построим вектор-строку с таким же количеством (это важно!) элементов v=(0:2*3.14/50:6.28);
Формируем для x(u,v) матрицу как матричное произведение столбца ch(u) и строки cos(v) то есть x=cosh(u)*cos(v) где cosh это косинус гиперболический на языке операторов МАТЛАБа.
Аналогично y=cosh(u)*sin(v);
После этого надо сформировать матрицу z как матричное произведение столбца sh(u) на строку единиц такой же длины. Для построения строки единиц такой же длины используем команду ones(size(v));
Таким образом z=sinh(u)*ones(size(v));
Затем формируем график поверхности surf(x,y,z);
Построим график движения точки на плоскости. Пусть она движется по кривой заданной параметрически. х(t)=cos(t), y(t)=3sin(t). Используем оператор comet(x,y). Он позволяет анимировать движение точки.
Движение точки вдоль винтовой линии заданной параметрически x(t)=sin(t), y(t)=cos(t), z(t)=t, можно смоделировать с помощью команды comet3(sin(t),cos(t),t);