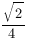Показать применение метода координат к решению задач на нахождение угла между скрещивающимися прямыми.
Угол между скрещивающимися прямыми - определение.
две прямые в трехмерном пространстве называются скрещивающимися, если они не лежат в одной плоскости.
Приведем еще вспомогательные рассуждения.
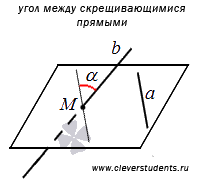
Пусть в трехмерном пространстве заданы две скрещивающиеся прямые a и b. Построим прямые a1 и b1 так, чтобы они были параллельны скрещивающимся прямым a и b соответственно и проходили через некоторую точку пространства M1. Таким образом, мы получим две пересекающиеся прямые a1 и b1. Пусть угол между пересекающимися прямыми a1 и b1 равен углу 
.
Угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым.
Из определения следует, что угол между скрещивающимися прямыми также не будет зависеть от выбора точки M. Поэтому в качестве точки М можно взять любую точку, принадлежащую одной из скрещивающихся прямых.
Нахождение угла между скрещивающимися прямыми.
Так как угол между скрещивающимися прямыми определяется через угол между пересекающимися прямым, то нахождение угла между скрещивающимися прямыми сводится к нахождению угла между соответствующими пересекающимися прямыми в трехмерном пространстве.
Несомненно, для нахождения угла между скрещивающимися прямыми подходят методы, изучаемые на уроках геометрии в средней школе. То есть, выполнив необходимые построения, можно связать искомый угол с каким-либо известным из условия углом, основываясь на равенстве или подобии фигур, в некоторых случаях поможет теорема косинусов, а иногда к результату приводит определение синуса, косинуса и тангенса угла прямоугольного треугольника.
|
|
удобно решать задачу нахождения угла между скрещивающимися прямыми методом координат.
Пусть в трехмерном пространстве введена прямоугольная система координат Поставим перед собой задачу: найти угол между скрещивающимися прямыми a и b, которым соответствуют в прямоугольной системе координат
Решим ее.
Возьмем произвольную точку трехмерного пространства М и будем считать, что через нее проходят прямые a1 и b1, параллельные скрещивающимся прямым a и b соответственно. Тогда искомый угол между скрещивающимися прямыми a и b равен углу между пересекающимися прямыми a1 и b1 по определению.
Таким образом, нам осталось найти угол между пересекающимися прямыми a1 и b1. Чтобы применить формулу для нахождения угла между двумя пересекающимися прямыми в пространстве нам нужно знать координаты направляющих векторов прямых a1 и b1.
Определение направляющего вектора прямой позволяет утверждать, что множества направляющих векторов параллельных прямых совпадают. Следовательно, в качестве направляющих векторов прямых a1 и b1 можно принять направляющие векторы 
и 
прямых a и b соответственно.
Координаты векторов 
и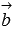 
определяются либо по известным из условия уравнениям прямых a и b (смотрите раздел координаты направляющего вектора прямой), либо по известным из условия координатам двух точек прямых a и b (здесь может быть полезна теория раздела координаты вектора через координаты точек его начала и конца).
Итак, угол между двумя скрещивающимися прямыми a и b вычисляется по формуле 
, где и - направляющие векторы прямых a и b соответственно.
|
|
Формула для нахождения косинуса угла между скрещивающимися прямыми a и b имеет вид 
.
за угол между прямыми принимают меньший из двух углов, образованный этими прямыми, поэтому косинус угла между прямыми должен быть больше нуля, и он равен модулю косинуса угла между направляющими векторами.
В правильной шестиугольной призме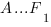
, все ребра которой равны 1, найти косинус угла между прямым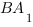и
и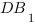
: 
1. Введем систему координат:
2. а) Найдем координаты направляющего вектора прямой 
, для этого найдем координаты точек 
и 
.
Длину отрезка 
найдем по тереме косинусов из треугольника 
:
; 
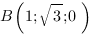
Чтобы найти координаты вектора 
, из координат конца вычтем координаты начала. Получим: 
б) Найдем координаты направляющего вектора прямой 
, для этого найдем координаты точек 
и 
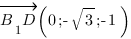
3. Найдем косинус угла 
между векторами и 
.
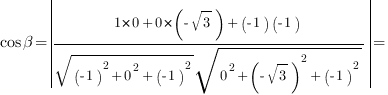
Ответ: 