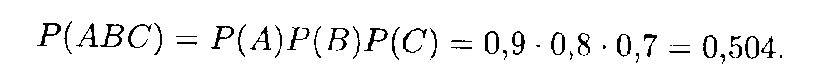Лекция 3. Теоремы сложения и умножения вероятностей. Повторение независимых испытаний Вопрос 1. Теорема сложения вероятностей
Несовместные события
Определение 1. Суммой двух событий А и В называют событие С = А + В, которое состоит в появлении либо события А, либо события В, либо событий A и В одновременно.
Пример: произведены два выстрела, события А и В — попадания при первом и втором выстрелах соответственно; тогда А + В — попадание либо при первом выстреле, либо при втором, либо в обоих выстрелах. Если события А и В несовместные, то их сумма — это событие, состоящее в появлении какого-либо из этих событий.
ТЕОРЕМА 1. Вероятность появления какого-либо из двух несовместных событий равна сумме вероятностей этих событий:
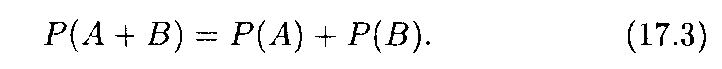
Следствие. Вероятность появления какого-либо из нескольких попарно несовместных событий равна сумме их вероятностей:
Пример 1. Стрелок стреляет по мишени, разделенной на 4 концентрические зоны. Вероятности попадания в эти области соответственно равны 0,4, 0,3, 0,2 и 0,1. Найти вероятность попадания либо в первую, либо во вторую зоны.
Решение. Пусть событие А — попадание в первую зону мишени, а событие В — попадание во вторую зону мишени. Эти события несовместны, поэтому применимы теорема.1 и формула (17.3) сложения вероятностей. Искомая вероятность равна
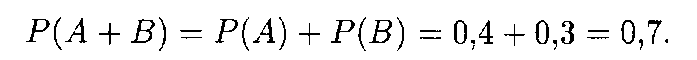
Полная группа событий
ТЕОРЕМА 2. Сумма вероятностей событий, образующих полную группу, равна единице:
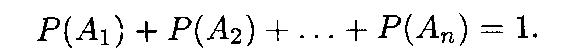
Пример 2. На складе готовой продукции находятся изделия, среди которых 5% нестандартных. Найти вероятность того, что при выдаче изделия со склада оно будет стандартным.
Решение. Вероятность получения нестандартного изделия равна 0,05; события выдачи стандартного и нестандартного изделия образуют полную группу. Следовательно, сумма их вероятностей равна единице, и тогда искомая вероятность равна 0,95.
Противоположные события
Определение 2. Два единственно возможных события, образующих полную группу, называются противоположными.
Если событие обозначено через А, то противоположное ему событие обозначается через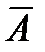 
. Из теоремы 2 следует, что
Например, если при стрельбе по мишени попадание — это событие А, то событие 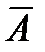— это промах; сумма их вероятностей равна единице — при выстреле обязательно будет либо попадание, либо промах. То же самое и при подбрасывании монеты: обязательно выпадет либо орел, либо решка.
Вопрос 2. Теорема умножения вероятностей
Произведение событий и условная вероятность
Определение 1. Произведением двух событий А и В называется событие АВ, означающее совместное появление этих событий.
Определение 2. Вероятность события В в предположении о наличии события А называют условной вероятностью РA(В).
ТЕОРЕМА 3. Вероятность произведения двух событий определяется формулой
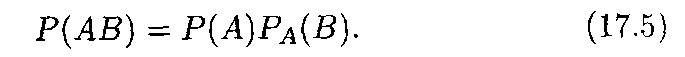
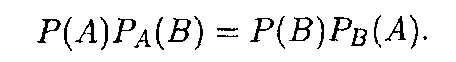
т
Пример 3. В урне находится 4 белых шара, 5 красных и 3 синих. Наудачу извлекают по одному шару, не возвращая его обратно. Найти вероятность того, что в первый раз появится белый шар (событие А), во второй раз — красный (событие В), в третий — синий (событие С).
Решение. Вероятность появления белого шара в первом извлечении Р(А) = 1/3; условная вероятность появления красного шара во втором извлечении при условии появления в первый раз белого шара РA(В) = 5/11; условная вероятность появления синего шара в третьем извлечении при условиях появления в предыдущих извлечениях белого и красного шаров РAB(С) = 0,3. Искомая вероятность:
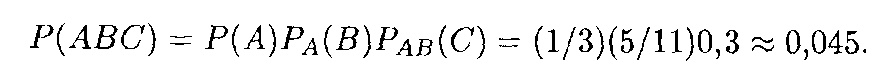
Независимые события
Определение 3. Событие В называется независимым от события А, если условная вероятность события В равна его безусловной вероятности (появление события А не влияет на вероятность события В):
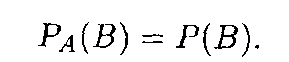
Отсюда следует, что и событие А также независимо от события В:
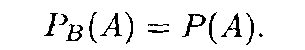
Для независимых событий теорема умножения вероятностей в общей форме имеет вид
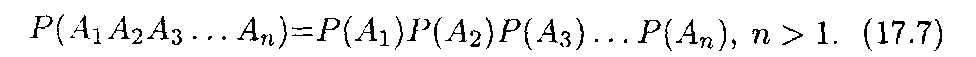
Пример 4. Найти вероятность поражения цели при совместной стрельбе тремя орудиями, если вероятности поражения цели орудиями соответственно равны 0,9, 0,8 и 0,7 (события А, B и С).
Решение. Поскольку события А, В и С являются независимыми, то искомая вероятность вычисляется, согласно формуле (17.7), при n = 3:
