Вопросы к зачету
1. Отрезок. Определение отрезка. Обозначение отрезка. Середина отрезка. Свойства длин отрезков.
2. Прямая и луч. Определение прямой и луча. Обозначение прямой и луча.
3. Угол. Определение угла. Обозначение угла. Биссектриса угла. Свойства градусных мер углов.
4. Смежные углы. Свойство смежных углов.
5. Вертикальные углы. Свойство вертикальных углов.
6. Признаки равенства треугольников.
7. Биссектрисы и медианы треугольника.
8. Высоты треугольника.
9. Равнобедренный треугольник. Свойства равнобедренного треугольника.
10. Окружность. Центр, радиус, диаметр, хорда окружности.
Вопросы к зачету
1. Отрезок. Определение отрезка. Обозначение отрезка. Середина отрезка. Свойства длин отрезков.
2. Прямая и луч. Определение прямой и луча. Обозначение прямой и луча.
3. Угол. Определение угла. Обозначение угла. Биссектриса угла. Свойства градусных мер углов.
4. Смежные углы. Свойство смежных углов.
5. Вертикальные углы. Свойство вертикальных углов.
6. Признаки равенства треугольников.
7. Биссектрисы и медианы треугольника.
8. Высоты треугольника.
9. Равнобедренный треугольник. Свойства равнобедренного треугольника.
10. Окружность. Центр, радиус, диаметр, хорда окружности.
ОТКРЫТЫЙ БАНК ЗАДАНИЙ К ЗАЧЁТУ ПО ГЕОМЕТРИИ
Класс
ЗАДАЧИ
Задачи на нахождение неизвестных величин.
1. Боковая сторона равнобедренного треугольника равна 19 см, а его периметр – 48 см. Найдите длину основания треугольника.
2. Периметр равнобедренного треугольника равен 60 см, а его основание в два раза меньше боковой стороны. Найдите стороны треугольника.
3. Один из смежных углов на 26о меньше другого. Найдите эти углы.
4. Один из смежных углов в 11 раз больше другого. Найдите эти углы.
5. Найдите все неразвёрнутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 296о.
6. На прямой а отложены точки М, К, N, причём МК = 7 см, КN = 10 см. Чему может быть равна длина отрезка МN?
7. Точка Е – середина отрезка СD, СЕ = 2,8 см. Найдите длину отрезка СD в миллиметрах.
8. Луч ОС делит угол АОВ на два угла. Найдите угол СОВ, если 
, а угол АОС на 18о меньше угла ВОС.
9. Отрезки АВ и С D – диаметры окружности с центром в точке О. Хорда АВ = 5см. Найдите длину хорды ВС.
10. На рисунке АВ = ВС, Ð ВАD = 105 
. Найдите Ð МСN.
В
D А С N
М
11. 
Углы, отмеченные на рисунке одной дугой, равны. Найдите угол α. Ответ дайте в градусах.
12. 
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB = 108°. Ответ дайте в градусах.
13. 
Для окаймления вымпела, имеющего форму равнобедренного треугольника, представленного на рисунке, необходимо закупить ленту, причём её длина должна быть в два раза больше периметра вымпела. Сколько рублей необходимо затратить на окаймление одного вымпела, если 1 м ленты стоит 48 руб.?
14. 
На асфальте нарисована дорожка в форме равнобедренного треугольника. Вася хочет пройти всю дорожку. По рисунку определите, сколько шагов необходимо сделать Васе, чтобы пройти всю дорожку.
Задачи на доказательство геометрических фактов
1. На основании ВС равнобедренного 
АВС отмечены точки М и N так, что ВМ = СN. Докажите, что ВАМ = САN.
2. 
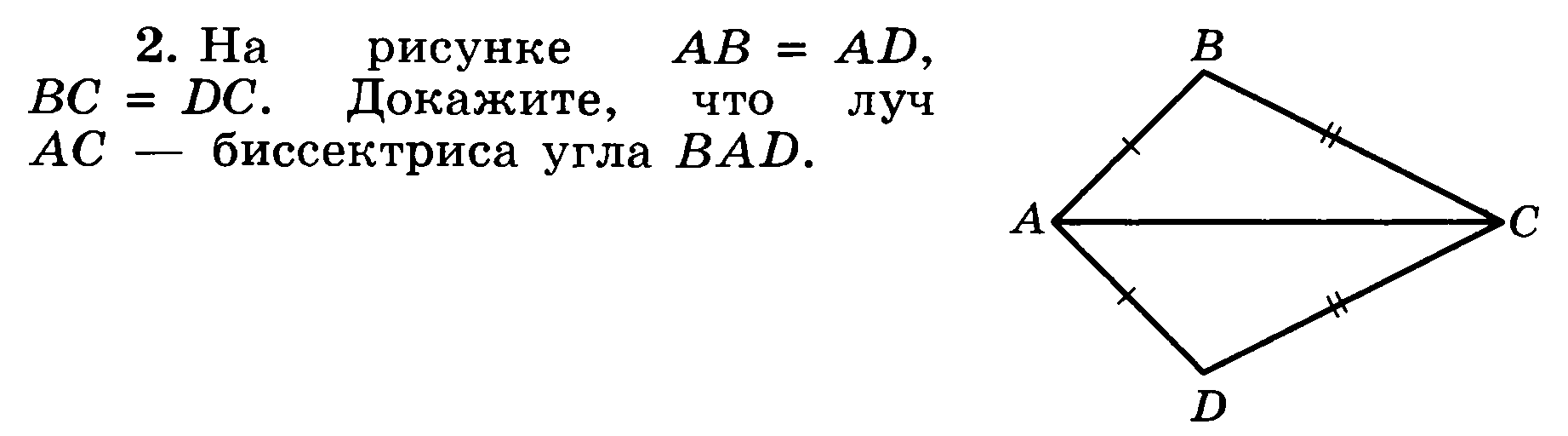На рисунке АВ = АD, ВС = DС. Докажите, что луч АС – биссектриса угла ВАD.
3. Докажите, что углы при основании равнобедренного треугольника, равны.
4. Докажите, что биссектриса, проведенная к основанию равнобедренного треугольника, является медианой и высотой.
5. Докажите, что высота, проведенная к основанию равнобедренного треугольника, является медианой и биссектрисой.
6. Докажите, что медиана, проведенная к основанию равнобедренного треугольника, является высотой и биссектрисой.
7. По данным рисунка докажите, что треугольники ТОР, ТОG и РОG равны.
8. Докажите, что в равностороннем треугольнике все углы равны.
9. На рисунке АВ = ВС, Ð1 = Ð2. Докажите, что
АDС – равнобедренный.
10. На продолжении медианы ВМ треугольника АВС отмечена точка D так, что ВМ = МD. Докажите равенство треугольников АМD и СМВ.
11. На сторонах угла на равном расстоянии от его вершины О отмечены точки М и N, а набиссектрисе данного угла – точка Р. Докажите равенство треугольников ОМР и ОNР.
12. В окружности с центром в точке О проведены два диаметра АВ и D С. Докажите, что хорды АС и ВD равны.
Выбор верного (неверного) утверждения:
1. Если угол равен 50°, то смежный с ним угол равен 50°.
2. Если один из вертикальных углов равен 80°, то другой угол равен 100°.
3. Угол называют тупым, если его градусная мера больше 90°.
4. Одна шестидесятая часть минуты называется секундой.
5. Если два угла с общей вершиной равны, то они вертикальные.
6. Треугольник называется равнобедренным, если его углы равны.
7. Вертикальные углы равны.
8. Два треугольника равны, если два угла одного треугольника равны двум углам другого треугольника
9. Периметр треугольника – это длина всех его сторон.
10. В равнобедренном треугольнике угол при основании может быть как острым, так и прямым или тупым.
11. Через любые три точки проходит ровно одна прямая.
12. Через любую точку проходит более одной прямой.
13. Если две прямые перпендикулярны третьей прямой, то эти две прямые перпендикулярны.
14. Смежные углы равны.
15. Любые две прямые имеют ровно одну общую точку.
16. Две прямые, перпендикулярные к третьей прямой, не пересекаются.
17. Неразвёрнутый угол меньше 180о.
18. Луч, исходящий из вершины угла, называется биссектрисой угла.
19. Сумма вертикальных углов равна 180о.
20. Отрезок биссектрисы угла треугольника называется биссектрисой треугольника.
21. Биссектрисы треугольника пересекаются в одной точке.
22. Все равносторонние треугольники равны.
23. Высота равнобедренного треугольника является медианой и биссектрисой.
24. Угол – это геометрическая фигура, состоящая из точки и двух лучей.
25. Прямые, содержащие высоты треугольника, пересекаются в трёх точках.
26. Два треугольника равны, если три стороны одного треугольника соответственно равны трём сторонам другого треугольника.
27. Диаметр окружности в два раза больше её радиуса.
28. Каждая из биссектрис равнобедренного треугольника является его высотой.
29. Два треугольника равны, если две стороны и угол одного треугольника равны двум сторонам и углу другого треугольника.
30. В равностороннем треугольнике периметр в три раза больше, чем сторона.
31. В равнобедренном треугольнике два угла равны.
32. В равностороннем треугольнике все углы равны.