Простой сдвиг
Ранее у нас шла речь о чистом сдвиге. Вспомним еще раз, что это такое.
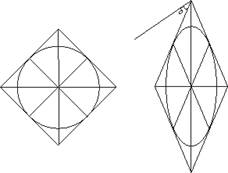
Рис. 1. Деформация чистого сдвига
Квадрат превращается в ромб. Оси эллипса деформации совпадают с осями ромба. Такой сдвиг, в принципе, можно охарактеризовать углом сдвига δ (это мера деформации прямого угла). При чистом сдвиге длины всех отрезков изменяются, а все точки (за исключением лежащих на осях деформации) движутся по криволинейным траекториям. Важно, что это соосная деформация, т.е. с оси деформации совпадают с осями напряжений.
Рассмотрим теперь простой сдвиг.
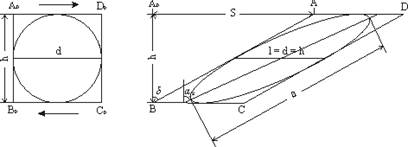
Рис. 2. Деформация простого сдвига
Здесь квадрат превращается в параллелограмм (при условии плоской деформации). Основание этого параллелограмма и его высота остаются равными сторонам первичного квадрата. Длинная ось эллипса деформации не совпадает с длинной диагональю параллелограмма. По определению, все точки тела, испытывающего деформацию простого сдвига, движутся параллельно одной прямой, или направлению сдвига, и проходят путь, прямо пропорциональный расстоянию от этой прямой.
Параметры, характеризующие простой сдвиг.
1. Угол сдвига δ (мера деформации прямого угла). Угол отсчитывается от перпендикуляра к направлению сдвига. Другими словами, это разница между первоначальным прямым углом и острым углом параллелограмма, после деформации.
2. Величина сдвига γ = S/ h = tgδ
3. Коэффициент деформации k = a/d
4. Угол наклона длинной оси эллипса деформации αk Угол отсчитывается от перпендикуляра к направлению сдвига.
Из определения простого сдвига следует, что в теле, испытывающем деформацию такого сдвига, существуют инвариантные линии. Это все линии, параллельные направлению сдвига. Их длина в процессе деформации не меняется, а все точки, лежащие на этих линиях, в процессе деформации проходят один и тот же путь. Из этого можно сделать также вывод, что максимальный диаметр эллипса деформации, параллельный направлению сдвига, равен диаметру первоначальной окружности и высоте параллелограмма.
Несмотря на свою «простоту», деформация простого сдвига не так тривиальна, как кажется. Прежде всего, эта деформация является несоосной. Здесь оси напряжений не совпадают по ориентировке с осями прогрессивной деформации. Оси напряжений в процессе деформации не меняют своей ориентировки, а оси деформации все время поворачиваются. В отличие от чистого сдвига, в котором длинная и короткая оси эллипса деформации все время представляют собой одни и те же материальные волокна и лишь меняют свою длину, при простом сдвиге это разные волокна. Иными словами, контур эллипса, представляющий собой геометрическое место материальных точек первоначального круга, в процессе деформации уподобляется гусенице трактора. Можно показать, что при простом сдвиге происходит сочетание собственно деформации и «внешнего» вращения (напомним, что при чистом сдвиге происходит лишь «внутреннее» вращение).
В природе существуют индикаторы вращения в зонах сдвига в виде жестких включений, например, таких:
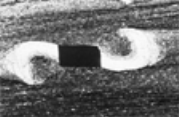
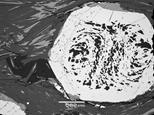
Рис. 3. Структуры, свидетельствующие о вращение в зоне сдвига
О том, как интерпретировать подобные структуры, будет сказано ниже.
Деформация простого сдвига очень широко распространена в природе. Это не только зоны сдвигов, где сдвиг понимается как разрыв со смещением по простиранию. Например, такая деформация может осуществляться и на крыльях складок, где нет никаких разрывов, но об этом тоже речь будет идти позже.