прямой, параллельны, лежат в одной

Прямые в пространстве. Пересекающиеся, параллельные, скрещивающиеся прямые

На плоскости две прямые или пересекаются, или параллельны друг другу. А в пространстве возможен еще один случай взаимного расположения прямых.

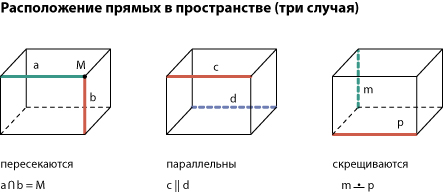
Две прямые в пространстве параллельны друг другу, пересекаются или скрещиваются.

Если две прямые параллельны третьей, то они параллельны друг другу.

Скрещивающиеся прямые не пересекаются и не параллельны друг другу. Через них невозможно провести плоскость. Скрещивающиеся прямые лежат в параллельных плоскостях.

 

 

Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Признак скрещивающихся прямых. Если одна из скрещивающихся прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

2. Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.

 

Первый признак

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.

То есть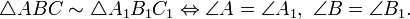

Дано: и

Доказать:

Доказательство

Второй признак

Если угол одного треугольника равен углу другого, а стороны, образующие тот угол в одном треугольнике, пропорциональны соответствующим сторонам другого, то такие треугольники подобны.

Третий признак

Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны.

Дано: ∆ABC и ∆A₁B₁C₁, = = .

Доказать: ∆ABC 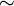∆A₁B₁C₁.

 

Билет №7

1. Если одна из двух параллельных прямых пересекает плоскость, то и другая пересекает эту плоскость.

Чертеж 2.1.3

Доказательство
Пусть a || b и a α = A (чертеж 2.1.3). Параллельные прямые a и b определяют некоторую плоскость β. Плоскости α и β имеют общую точку A, а, следовательно, имеют и общую прямую c, проходящую через точку A по аксиоме 1.2. Через точку A можно провести только одну прямую a, параллельную b. Следовательно, c не параллельна b. Прямые b и c не параллельны и лежат в одной плоскости β, следовательно, пересекаются в некоторой точке B. Прямая b имеет с плоскостью α общую точку B и не лежит в плоскости α (иначе по теореме 2.2 a и b были бы скрещивающимися). Следовательно, прямая b пересекает плоскость α. Лемма доказана.

2. Доказанные в предыдущем пункте теоремы дают возможность выразить площадь треугольника через три его стороны:
,
где , , — стороны треугольника и 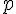— его полупериметр. Эту формулу называют формулой Герона. Доказательство ее будем вести одновременно для остроугольного и тупоугольного треугольников.

Формула Герона выражает площадь треугольника через длины трех его сторон.

Теорема (формула Герона). Площадь треугольника со сторонами a, b, c и полупериметром p равна выражению:

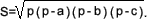
Доказательство. Пусть O - центр вписанной в треугольник ABC окружности, r - ее радиус

.

Соединив центр O с вершинами A, B и C, получим треугольники AOC, BOC и AOB с высотами, равными r.

Согласно свойству площадей:
пл. треугольника ABC=пл. треугольника AOC+пл. треугольника AOB+пл. треугольника BOC=
= 1/2 b ^. r+1/2 c ^. r+1/2 a ^. r=r/2 (a+b+c)=p ^. r.

Выражая r через стороны треугольника a, b и с, получаем

Тогда ,
что и требовалось доказать.

 

 

Билет №8

1. В большинстве школьных учебников две прямые называются параллельными, если они лежат в одной плоскости и не имеют ни одной общей точки. После этой определения доказывается теорема о существовании и единственности прямой в пространстве, проходящей через данную точку параллельно данной прямой.

Если считать параллельными и совпадающие прямые, то
множество всех параллельных прямых в пространстве можно разбить на непересекающиеся классы параллельных между собой прямых, так как праллельность прямых в пространстве есть отношение эквиалентности, в частности, выполняется транзитивность: если и , то .

Если же совпадающие прямые не считать параллельными, то верна такая теорема (отличающаяся от того, что мы называем транзитивностью):

Если две различные прямые параллельны третьей, то они параллельны между собой.

 

Свойства медиан

§ Медианы треугольника пересекаются в одной точке, которая называется центроидом

, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

§ Треугольник делится тремя медианами на шесть равновеликих треугольников.

§ Большей стороне треугольника соответствует меньшая медиана.

§ Из векторов, образующих медианы, можно составить треугольник.

§ При аффинных преобразованиях медиана переходит в медиану.

§ Медиана треугольника делит его на две равновеликие части.

Точку пересечения медиан треугольника называют центром тяжести или центром масс. Оказывается, если поместить в вершины треугольника равные массы, то их центр попадет в эту точку. Центр равных масс иногда называют центроидом. В этой же точке располагается и центр масс однородной треугольной пластинки. Если подобную пластинку поместить на булавку так, чтобы острие последней попало точно в центроид, то пластинка будет находиться в равновесии. Проделай этот опыт и убедись в справедливости данного утверждения.

 

Билет №9

1. Лучи ОА и О₁А₁ не лежат на одной

прямой, параллельны, лежат в одной

полуплоскости с границей ОО₁ →

Сонаправленные

 

Свойства биссектрис

§ Теорема о биссектрисе: Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон

§ Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.

§ Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.

§ Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника.

§ Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой.

§ Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса).

§ Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно, ^[2] причём даже при наличии трисектора. ^[3]

 

Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.

Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.

Центр O вписанной окружности называется инцентром, он равноудалён от всех сторон и является точкой пересечения биссектрис треугольника.

 

Билет №10

1. Построение

Срединный перпендикуляр

Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.

Свойства серединных перпендикуляров треугольника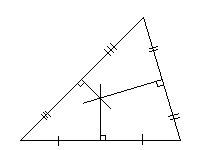

1. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

2. Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

Ортоцентр (от греч. ορθοξ — прямой) — точка пересечения высоттреугольника или их продолжений. Традиционно обозначается латинской буквой H. В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольных), вне его (в тупоугольных) или совпадать с вершиной (в прямоугольных — совпадает с вершиной при прямом угле).

§ Если в четвёрке точек A, B, C, D точка D является точкой пересечения высот треугольника ABC, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек.

§ Радиусы окружностей, проходящих через любые три точки ортоцентрической системы, равны.

§ Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).

§ Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.

§ Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.

§ Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.

§ Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.

§ Если О — центр описанной окружности ΔABC, то ,

§ , где — радиус описанной окружности; 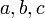— длины сторон треугольника.

§ Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.

§ При изогональном сопряжении ортоцентр переходит в центр описанной окружности.

Описанная окру́жность многоугольника — окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать ) пересечения серединных перпендикуляров к сторонам многоугольника.

Содержание [ убрать ] · 1 Свойства o 1.1 Для треугольника § 1.1.1 Радиус § 1.1.2 Положение центра описанной окружности § 1.1.3 Уравнение описанной окружности o 1.2 Для четырехугольника o 1.3 Для многоугольника o 1.4 В сферическом треугольнике · 2 См. также · 3 Примечания · 4 Литература

[ править ]Свойства

§ Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).

§ Около любого правильногомногоугольника можно описать окружность, и притом только одну.

[ править ] Для треугольника

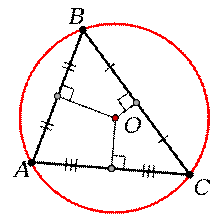
Окружность, описанная около треугольника

§ Около треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров.

§ У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.

§

Остроугольный

 

§

Тупоугольный

 

§

Прямоугольный

Обозначаем буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА = OB = ОС. Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника ABC.

§ 3 из 4 окружностей, описанных относительно серединных треугольников (образованных средними линиями треугольника), пересекаются в одной точке внутри треугольника. Эта точка и есть центр описанной окружности основного треугольника.

§ Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.

§ Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.

[ править ] Радиус

Радиус описанной окружности может быть найден по формулам

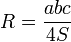
Где:

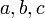— стороны треугольника,

— угол, лежащий против стороны ,

— площадь треугольника.

— полупериметр треугольника.