В реальном трансформаторе кроме основного магнитного потока Ф, который замыкается по стали и сцеплен со всеми обмотками трансформатора, имеются также потоки рассеяния Фσ1 и Фσ2, сцепленные только с одной из обмоток.
Потоки рассеяния не участвуют в передаче энергии, но создают в каждой из обмоток соответствующие ЭДС самоиндукции.
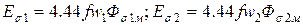
С учетом этих ЭДС и падений напряжения в активных сопротивлениях обмоток можно составить комплексные уравнения для первичной и вторичной обмоток трансформатора
С учетом 
получаем систему уравнений:
где 
- сопротивление нагрузки, подключенной к трансформатору.
Т.к. потоки рассеяния полностью или частично замыкаются по воздуху, то они пропорциональны МДС соответствующих обмоток или соответствующими токами:
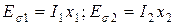
величины х1 и х2 называют индуктивными сопротивлениями обмоток трансформатора, обусловленными потоками рассеяния.
Т.к. векторы ЭДС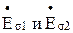 
отстают от соответствующих потоков и токов на 900, то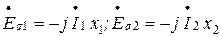 
При этом комплексные управления трансформатора примут вид
Замена ЭДС 
падениями напряжений 
показывает значение потоков рассеяния: они создают индуктивные падения напряжений в обмотках, не участвуя в передаче энергии из одной обмотки в другую.
Проще становится и построение векторной диаграммы соответствующей системе уравнений, в которой целесообразно также заменить падение напряжения в нагрузке величины 
, т.е. вторичным напряжением трансформатора из формулы 2
(4)
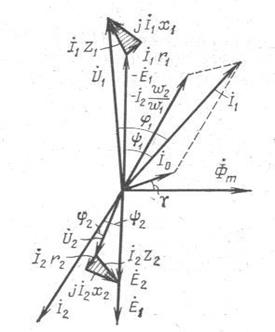
Векторную диаграмму вторичной обмотки трансформатора строим согласно уравнению 4. Характер диаграммы определяется током нагрузки 
, которая принимается заданным по величине и фазе. Итак, задаваясь векторами вторичного тока .(например для активно-индуктивной нагрузки)
МДС 
оказывает своей реактивной составляющей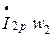 
на магнитопровод размагничивающее действие:
- реактивная составляющая тока нагрузки.
Построение диаграммы начинаем с вектора максимального значения основного магнитного потока 
. Вектор тока 
опережает по фазе вектор потока 
на угол γ=5..100. Вектор 
как и 
отстают от потока на 900. [ - приведенная вторичная ЭДС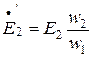 
]. Для определения угла сдвига фаз между и определим характер нагрузки трансформатора:(
) активно-индуктивная, тогда вектор отстает по фазе от 
на угол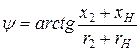 
, определяемый как характером внешней нагрузки, так и собственным сопротивлением вторичной обмотки.
Чтобы построить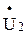 
из вектора 
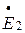вычитаем 
Построив вектор 
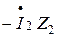получили треугольник внутренних падений напряжения во вторичной цепи. Затем из т.О проводим вектор 
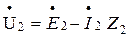, который опережает по фазе ток 
на угол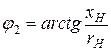 
.
Вектор первичного тока строили как сумму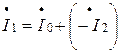 
. Строим 
, для чего к вектору 
, опережающему по фазе вектор потока Фm на 900, прибавляем векторы внутренних падений напряжения первичной обмотки: вектор 
, 
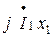опережает 
на 900, Соединяя таким образом с концом вектора 
получим вектор 
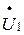, который опережает вектор 
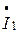на φ1. Когда векторная диаграмма трансформатора строят с целью определения ЭДС, то заданными являются параметры U2, I2, Cosφ2. Зная 
определяют 
и строят векторы, под фазовым углом φ2.
Т.к. ток отстает по фазе от ЭДС 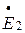на угол φ2, то в случае активно-емкостной нагрузки, когда 
и ток нагрузки опережает по фазе ЭДС 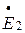на угол φ2. Векторная диаграмма имеет вид отличный от акт-инд. нагрузки.
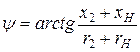
При значительной емкостной составляющей нагрузки падение напряжения в емкостной составляющей сопротивления нагрузки и индуктивное падение напряжение рассеяния во вторичной обмотке частично компенсируют друг друга. В результате 
может оказаться больше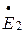 
. Реактивная составляющая вторичного тока 
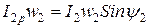совпадает по фазе с реактивной составляющей тока х.х. 
, т.е. оказывает на магнитопровод подмагничивающее действие.