ЗАДАЧА В-8
| 1.Прототип задания 8 (№ 119972) |
Прямая 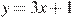 является касательной к графику функции является касательной к графику функции 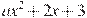 . Найдите a. . Найдите a.
|
Решение.
Прямая 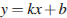 является касательной к графику функции
является касательной к графику функции 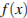 в точке
в точке 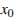 тогда и только тогда, когда одновременно
тогда и только тогда, когда одновременно 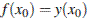 и
и 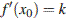 . В нашем случае имеем:
. В нашем случае имеем:
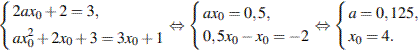
Искомое значение а равно 0,125
Ответ: 0,125.
Приведем другое решение.
По смыслу задачи a ≠ 0, а значит, график заданной функции — парабола. Касательная к параболе (а также и к гиперболе) имеет с ней единственную общую точку. Поэтому необходимо и достаточно, чтобы уравнение 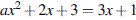 имело единственно решение. Для этого дискриминант
имело единственно решение. Для этого дискриминант 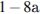 уравнения
уравнения 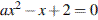 должен быть равен нулю, откуда
должен быть равен нулю, откуда  .
.
Ответ: 0,125
Ответ:a= 0,125
| 2. Прототип задания 8 (№ 119973) |
Прямая 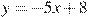 является касательной к графику функции является касательной к графику функции  . Найдите b, учитывая, что абсцисса точки касания больше 0. . Найдите b, учитывая, что абсцисса точки касания больше 0.
|
Решение.
Условие касания графика функции 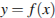 и прямой
и прямой  задаётся системой требований:
задаётся системой требований:

В нашем случае имеем:
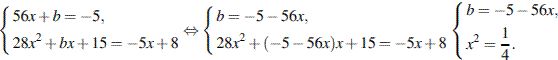
По условию абсцисса точки касания положительна, поэтому x =0,5, откуда b =−33.
Ответ: −33.
3. Прототип задания 8 (№ 119974) Прямая  является касательной к графику функции
является касательной к графику функции 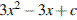 . Найдите
. Найдите 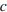 .
.
Решение.
Условие касания графика функции 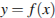 и прямой
и прямой 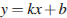 задаётся системой требований:
задаётся системой требований:
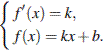
В нашем случае имеем:
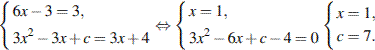
Ответ: 7.
Прототип задания 8 (№ 119975)
Материальная точка движется прямолинейно по закону  , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, 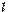 — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени
— время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени  с.
с.
Решение.
Найдем закон изменения скорости:
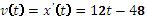
При t = 9 c имеем:

Ответ: 60
Прототип задания 8 (№ 119976)
Материальная точка движется прямолинейно по закону  , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, 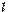 — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени
— время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени  с.
с.
Решение.
Найдем закон изменения скорости:

При t = 6 c имеем:

Ответ: 20.
Прототип задания 8 (№ 119977)
Материальная точка движется прямолинейно по закону 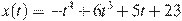 , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, 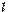 — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени
— время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени  с.
с.
Решение.
Найдем закон изменения скорости:
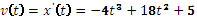
При t = 3 c имеем:
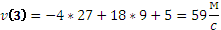
Ответ: 59.
Прототип задания 8 (№ 119978)
Материальная точка движется прямолинейно по закону  , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, 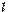 — время в секундах,
— время в секундах,  измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Берем производную от  ,получаем
,получаем 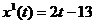
Приравниваем полученное уравнение к необходимой нам скорости,заданной в условии (3)
Получаем:
2t-13=3
2t-13+3=0
2t-10=0
2t= 10
t=10/2
t=5
Ответ = 5
Прототип задания 8 (№ 119979)
Материальная точка движется прямолинейно по закону 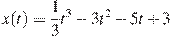 , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, 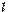 — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
— время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Берем производную от 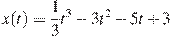
Получаем: 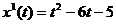
Приравниваем полученное уравнение к необходимой нам скорости,заданной в условии
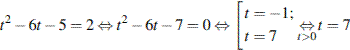
Ответ: 7
Прототип задания 8 (№ 317539)
На рисунке изображён график функции  и восемь точек на оси абсцисс:
и восемь точек на оси абсцисс: 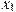 ,
, 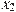 ,
,  ,
,  ,
,  . В скольких из этих точек производная функции
. В скольких из этих точек производная функции 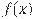 положительна?
положительна?
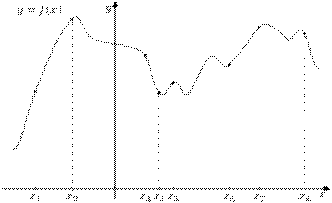
Если функция возрастает, то производная положительна, если функция убывает, то производная отрицательна. Поэтому производная данной функции положительна в точках x1;x2;x5;x6;x7 => Ответ: в 5 точках.
Прототип задания 8 (№ 317540)
На рисунке изображён график функции  и двенадцать точек на оси абсцисс:
и двенадцать точек на оси абсцисс: 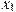 ,
, 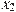 ,
,  ,
, 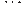 ,
, 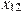 . В скольких из этих точек производная функции
. В скольких из этих точек производная функции 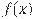 отрицательна?
отрицательна?
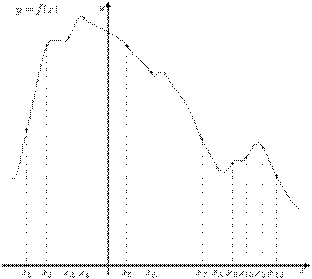
Если функция возрастает, то производная положительна, если функция убывает, то производная отрицательна. Поэтому производная данной функции отрицательна в точках x4;x5;x6;x7x8;x11;x12 => Ответ: в 7 точках.
11. Прототип задания 8 (№ 317541)
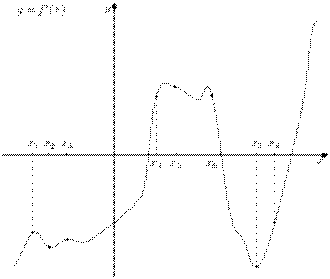
На рисунке изображён график  — производной функции — производной функции 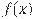 . На оси абсцисс отмечено восемь точек: . На оси абсцисс отмечено восемь точек: 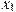 , , 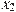 , ,  , ,  , ,  . Сколько из этих точек лежит на промежутках возрастания функции . Сколько из этих точек лежит на промежутках возрастания функции  ? ?
| |
|
Чтобы определить промежуток возрастания функции по графику ее производной надо найти промежуток, на котором производная больше нуля То есть нам необходимо выделить все точки, которые лежат ВЫШЕ оси OX, а это x4; x5; x6 => Ответ: 3
Прототип задания 8 (№ 317542)
На рисунке изображён график  — производной функции
— производной функции  . На оси абсцисс отмечено восемь точек:
. На оси абсцисс отмечено восемь точек: 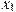 ,
, 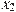 ,
,  ,
, 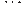 ,
,  . Сколько из этих точек лежит на промежутках убывания функции
. Сколько из этих точек лежит на промежутках убывания функции 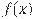 ?
?

Чтобы определить промежуток убывания функции по графику ее производной, надо найти промежуток, на котором производная меньше нуля То есть, нам необходимо выделить все точки, которые лежат НИЖЕ оси OX, а это x1;x2;x3;x4;x8 => Ответ: 5
Задание 8 (№ 27498)
На рисунке изображен график 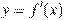 — производной функции
— производной функции 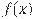 , определенной на интервале
, определенной на интервале  . Найдите промежутки убывания функции
. Найдите промежутки убывания функции 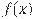 . В ответе укажите сумму целых точек, входящих в эти промежутки.
. В ответе укажите сумму целых точек, входящих в эти промежутки.
 Ход решения:
Ход решения:
Промежутки убывания функции f(x) соответствуют промежуткам, на которых производная функции отрицательна (график производной лежит ниже оси ОХ), то есть интервалу (−2,5; 6,5). Данный интервал содержит следующие целые точки: –2, –1, 0, 1, 2, 3, 4, 5, 6. Чтобы найти ответ на задание необходимо сложить эти точки.
-2+(-1)+0+1+2+3+4+5+6=18
Ответ: 18.
Задание 8 (№ 27499)
На рисунке изображен график 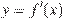 — производной функции
— производной функции 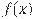 , определенной на интервале
, определенной на интервале 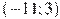 . Найдите промежутки возрастания функции
. Найдите промежутки возрастания функции 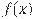 . В ответе укажите длину наибольшего из них.
. В ответе укажите длину наибольшего из них.
 Ход решения:
Ход решения:
Промежутки возрастания функции f(x) соответствуют промежуткам, на которых производная функции положительна(график производной лежит выше оси ОХ),, то есть интервалам (−11; −10), (−7; −1), (2; 3). Находим наибольший из них. Наибольшему соответствует интервал (-7:-1),длина которого 6.
Ответ: 6
15.Задание 8 (№ 27500)
На рисунке изображен график 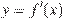 — производной функции
— производной функции 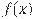 , определенной на интервале
, определенной на интервале 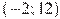 . Найдите промежутки убывания функции
. Найдите промежутки убывания функции 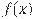 . В ответе укажите длину наибольшего из них.
. В ответе укажите длину наибольшего из них.
 ход решения:
ход решения:
Промежутки убывания функции f(x) соответствуют промежуткам, на которых производная функции отрицательна, то есть интервалам (−1; 5) длиной 6 и (7; 11) длиной 4. Длина наибольшего из них 6.
Ответ: 6
Задание 8 (№ 27501)
На рисунке изображен график 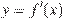 — производной функции
— производной функции 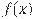 , определенной на интервале
, определенной на интервале  . Найдите количество точек, в которых касательная к графику функции
. Найдите количество точек, в которых касательная к графику функции 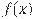 параллельна прямой
параллельна прямой  или совпадает с ней.
или совпадает с ней.
Ход решения: 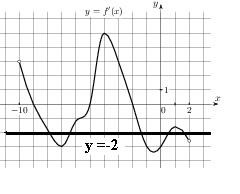 Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой y = −2 x − 11 или совпадает с ней, их угловые коэффициенты равны –2. Теперь нам необходимо найти количество точек, в которых y' (x 0) = −2, это соответствует количеству точек пересечения графика производной с прямой y = −2. На данном интервале таких точек 5.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой y = −2 x − 11 или совпадает с ней, их угловые коэффициенты равны –2. Теперь нам необходимо найти количество точек, в которых y' (x 0) = −2, это соответствует количеству точек пересечения графика производной с прямой y = −2. На данном интервале таких точек 5.
Ответ: 5
17. Задание 8 (№ 27499)
На рисунке изображен график 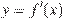 — производной функции
— производной функции 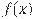 , определенной на интервале
, определенной на интервале 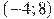 . Найдите точку экстремума функции
. Найдите точку экстремума функции 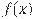 , принадлежащую отрезку
, принадлежащую отрезку 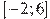 .
.
 Ход решения:
Ход решения:
Если производная в некоторой точке равна нулю, а в ее окрестности меняет знак, то это точка экстремума. На отрезке [–2; 6] график производной пересекает ось абсцисс, производная меняет знак с плюса на минус. Значит, точка 4 является точкой экстремума.
Ответ: 4
Задание 8 (№ 27503)
На рисунке изображены график функции 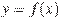 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 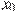 . Найдите значение производной функции
. Найдите значение производной функции 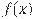 в точке
в точке 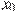 .
.
 Ход решения:
Ход решения:
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Строим треугольник с вершинами в точках A (1; 2), B (1; −4), C(−2; −4). Угол наклона касательной к оси абсцисс будет равен тангенсу угла ACB: 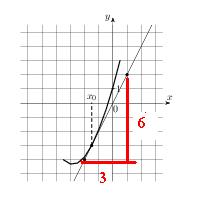
Y’(X0) = tg ACB=  =
= 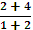 = 2
= 2
Ответ: 2
19. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 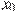 . Найдите значение производной функции
. Найдите значение производной функции 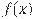 в точке
в точке 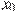 .
.



|






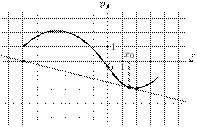
20. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 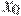 . Найдите значение производной функции
. Найдите значение производной функции 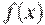 в точке
в точке 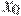 .
.
|






|
 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 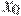 . Найдите значение производной функции
. Найдите значение производной функции 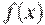 в точке
в точке 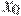 .
.






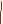

|
 — производной функции
— производной функции 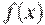 . Найдите абсциссу точки, в которой касательная к графику
. Найдите абсциссу точки, в которой касательная к графику  параллельна прямой
параллельна прямой  или совпадает с ней.
или совпадает с ней.
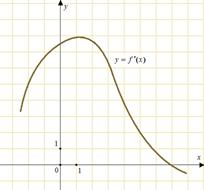
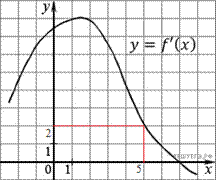
23.На рисунке изображен график 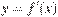 — производной функции
— производной функции  . Найдите абсциссу точки, в которой касательная к графику
. Найдите абсциссу точки, в которой касательная к графику  параллельна оси абсцисс или совпадает с ней.
параллельна оси абсцисс или совпадает с ней.
|




 24.На рисунке изображен график функции
24.На рисунке изображен график функции 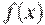 , определенной на интервале
, определенной на интервале  . Найдите количество точек, в которых производная функции
. Найдите количество точек, в которых производная функции 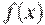 равна 0.
равна 0. 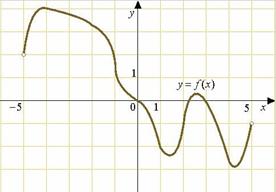

Производная равна нулю в точках экстремума. Ответ:425. Задание (№ 27485)
Прямая  параллельна касательной к графику функции
параллельна касательной к графику функции  . Найдите абсциссу точки касания.
. Найдите абсциссу точки касания.
Необходимо найти X1 точки с координатами (X1;Y1)
Касательная к функции  параллельна
параллельна  , значит её формула
, значит её формула
y=7x+n.
Производная квадратичной функции в точке X1 равна коэффициэнту k при x в функции y=7х+n (то есть 7)
Берём производную и приравниваем её к семи.
2x+6=7
2х=1
x=0.5
X1=0.5
Задание 8 (№ 27486)
Прямая 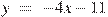 является касательной к графику функции
является касательной к графику функции  . Найдите абсциссу точки касания.
. Найдите абсциссу точки касания.
Необходимо найти абсциссу точки (X1;Y1)
Производная кубической функции в точке X1 равна коэффициэнту k при x в функции
y=-4х-11 (то есть -4)
Значит 3x2+14x+7=-4
3x2+14x+11=0
D=196-132=64=8*8
X1=(-14+8)/6=-6/6=-1
X2=(-14-8)/6=-22/6 –это значение не подходит по формату записи ответов в ЕГЭ
Подставляем X1 в оба уравнения
y=-4*(-1)-11=4-11=-7
y= (-1)3+7*(-1)2+7*(-1)-6=-1+7-7-6=-7
Функции равны в точке X1
Значит искомая нами абсцисса равна -1
Задание 8 (№ 27487)
На рисунке изображен график функции  , определенной на интервале
, определенной на интервале 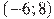 . Определите количество целых точек, в которых производная функции положительна.
. Определите количество целых точек, в которых производная функции положительна.
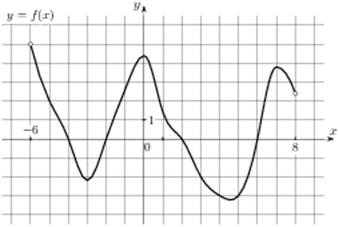 |
Производная положительна при возрастании функции
Выделим целые точки на оси х где функция возрастает
Это -2;-1;5;6. Всего 4 целых точки
Задание 8 (№ 27488)
На рисунке изображен график функции  , определенной на интервале
, определенной на интервале  . Определите количество целых точек, в которых производная функции
. Определите количество целых точек, в которых производная функции  отрицательна.
отрицательна.
Производная положительна при убывании функции
Выделим целые точки на оси х, где функция убывает
Это точки -4;-3;-2;-1;0;1;3;4. Всего 8 целых точек
Задание 8 (№ 27489)
На рисунке изображен график функции  , определенной на интервале
, определенной на интервале  . Найдите количество точек, в которых касательная к графику функции параллельна прямой
. Найдите количество точек, в которых касательная к графику функции параллельна прямой 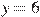 или совпадает с ней.
или совпадает с ней.
 |
y=6 – прямая параллельная оси OX
Касательные к графику параллельны оси ОХ,когда они касаются точек экстремума (коэффициент k у прямой y=k*x+n должна быть равна нулю, и этот же коэффициент равен производной в этой точке, а при производной равной нулю точка-экстремум)
Посчитаем сколько точек экстремума у функции, это и есть наш ответ.
Таких точек 4, ответ: 4
30.(№ 27490)
 |
На рисунке изображен график функции
 , определенной на интервале
, определенной на интервале 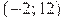 . Найдите сумму точек экстремумов функции
. Найдите сумму точек экстремумов функции 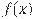 .Суммой точек экстремума называется сумма абсцисс, координат точек экстремума
.Суммой точек экстремума называется сумма абсцисс, координат точек экстремума
У нас 7 точек 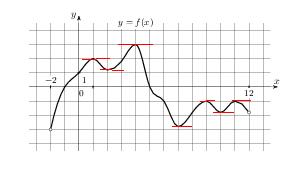
Складываем их абсциссы
1+2+4+7+9+10+11=44
Ответ:44
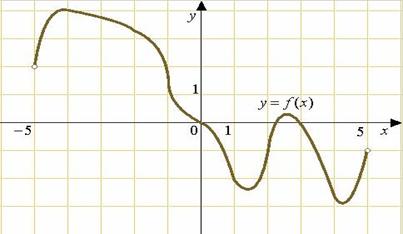
37. На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
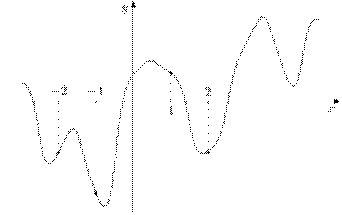
Нам известно, что если функция возрастает, то производная положительна, а если функция убывает, то производная отрицательна. Отсюда можем сделать вывод, что точки -1 и 1 не подходят. f’(x)=k=tg α,следовательно, необходимо сравнить угол наклона к оси ОХ в точке -2 и 2. Построив касательные, увидим, что в точке -2 угол больше, значит, в этой точке производная принимает наибольшее значение. 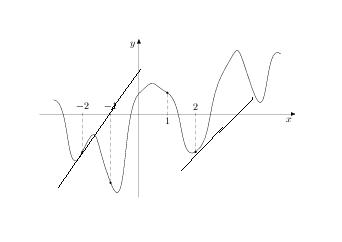
Ответ: -2
38. На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

Нам известно, что если функция возрастает, то производная положительна, а если функция убывает, то производная отрицательна. Делаем вывод, что точки -2 и 1 не подходят.. f’(x)=k=tg α,следовательно, необходимо сравнить тангенсы углов наклона к оси ОХ в точке -1 и 4. Построив касательные, увидим, что в точке 4 угол меньше, значит, в этой точке производная принимает наименьшее значение
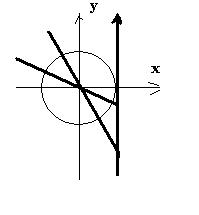 .
. 
Ответ: 4
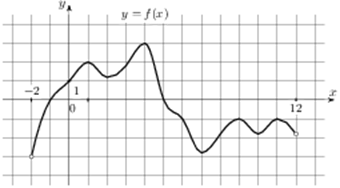
39. На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-3;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-2;4].

F(x) первообразная для f’(x), если F’(x) = f(x). По условию f(x)=0 => F’(x) =0. А это значит, что надо посмотреть количество экстремумов данной функции на заданном интервале. 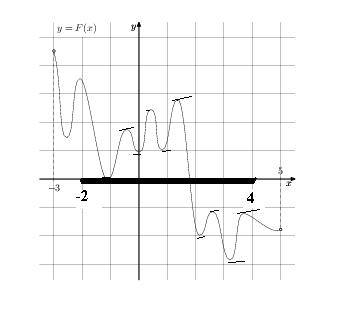
Ответ: 10
40. На рисунке изображён график функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8)-F(2), где F(x) — одна из первообразных функции f(x).

Для данной задачи нам необходимо будет вычислить площадь фигура на рисунке на указанном интервале. Получается, что площадь трапеции будет равна: 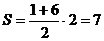
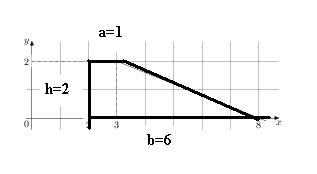
Ответ: 7
41. На рисунке изображён график некоторой функции y=f(x). Функция 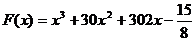 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

Для решения данной задачи необходимо знать, что определенный интеграл равен площади закрашенной фигуры. 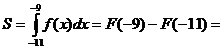
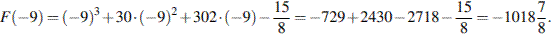

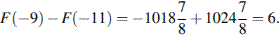
42. На рисунке изображён график некоторой функции 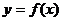 . Функция
. Функция  — одна из первообразных функции
— одна из первообразных функции 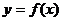 . Найдите площадь закрашенной фигуры.
. Найдите площадь закрашенной фигуры.

Для решения данной задачи необходимо знать, что определенный интеграл равен площади закрашенной фигуры. 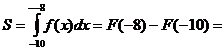 4
4
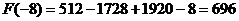

Ответ:4
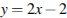 или совпадает с ней, она имеет угловой коэффициент равный 2 и
или совпадает с ней, она имеет угловой коэффициент равный 2 и 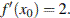 Осталось найти, при каких
Осталось найти, при каких 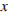 производная принимает значение 2. Искомая точка
производная принимает значение 2. Искомая точка  .
.
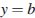 , и её угловой коэффициент равен 0. Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс. Поэтому искомая точка
, и её угловой коэффициент равен 0. Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс. Поэтому искомая точка 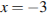 .
.