Задачи (будут на экзамене)
1. Предприниматель получил на полтора года кредит в размере 20 тыс. руб. с условием возврата 25 тыс. руб. Определите процентную и учетную ставки за полтора года.
Решение:
1. Процентная ставка (норма прибыли, доходность, рост за время t) – отношение результативности сделки к исходной сумме.
Базовая формула 
, где
PV – исходная сумма (20 тыс. рублей);
FV – возвращаемая сумма (25 тыс. рублей).
Получаем 
2. Учетная ставка (дисконтная ставка, дисконт за время t) – отношение результативности сделки к возвращаемой сумме.
Базовая формула 
, где
PV – исходная сумма (20 тыс. рублей);
FV – возвращаемая сумма (25 тыс. рублей).
Получаем 
Проверка.
При rt > 0, 0 < dt < 1, rt > dt справедливы соотношения:
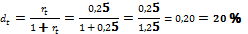
2. Определите доходность в виде процентной ставки за предоставление потребительского кредита на следующих условиях: 45% стоимости покупок оплачивается сразу, а через год вносится оставшаяся часть стоимости покупок и 10% от стоимости покупок в качестве платы за кредит.
Решение:
Процентная ставка (норма прибыли, доходность, рост за время t) – отношение результативности сделки к исходной сумме.
Базовая формула , где
PV – исходная сумма (0,55x = x -0,45x);
FV – возвращаемая сумма (0,65x = 0,55x +0,10x).
Получаем 
3. Предпринимателю 14 февраля предоставлена ссуда в размере 20 тыс. руб. с погашением 14 июля того же года под процентную ставку 30% годовых. Рассчитайте различными способами сумму к погашению, если начисляются простые проценты и год невисокосный.
Решение:
Предпринимателю предоставлена краткосрочная ссуда.
Базовая формула 
, где
Rn – возвращаемая сумма, сумма погашения (искомое);
P – исходная сумма, размер ссуды (20 тыс. рублей);
|
|
t – срок предоставления ссуды, в днях (определяется 3-мя способами, причем день выдачи и день погашения, считаются за один день);
T – количество дней в году (определяется двумя способами);
r – годовая процентная ставка (30 %).
1) Английская практика. Используется точное количество дней в году (T = 365 дней), с точным числом дней ссуды (t = 195 – 45 = 150 дней – по таблице)
Получаем 
2) Французская практика. Используется коммерческий год (T = 360 дней), с точным числом дней ссуды (t = 195 – 45 = 150 дней – по таблице)
Получаем 
3) Немецкая практика. Используется коммерческий год (T = 360 дней), с приближенным числом дней ссуды – месяц считается равным 30 дням (t = 30 дней*5 месяцев = 150 дней)
Получаем
4. На какой срок необходимо поместить денежную сумму под простую процентную ставку 28% годовых, чтобы она увеличилась в 1,5 раза?
Решение:
Используем расчет наращения простыми процентами.
Базовая формула 
, где
Rn – возвращаемая сумма (1);
P – исходная сумма (1,5);
n – число лет начисления процентов (искомое);
r – годовая процентная ставка (28 %).
Преобразуем исходную формулу для вычисления неизвестного (n).
Получаем 
1,786 года
5. В финансовом договоре клиента с банком предусмотрено погашение долга в размере 8,9 тыс. руб. через 120 дней при взятом кредите в 8 тыс. руб. Определить доходность такой сделки для банка в виде годовой процентной ставки. При начислении банк использует простые обыкновенные проценты.
Решение:
Используем расчет наращения при краткосрочной ссуде.
Базовая формула , где
Rn – возвращаемая сумма, сумма погашения (8,9 тыс. рублей);
|
|
P – исходная сумма, размер ссуды (8 тыс. рублей);
t – срок предоставления ссуды, в днях (120 дней);
T – количество дней в году (поскольку год не определен используем длительность коммерческого года - 360 дней);
r – годовая процентная ставка (искомое).
Преобразуем исходную формулу для вычисления неизвестного (r).
Получаем 
,3375 = 33,75%
6. Из какого капитала можно получить 24 тыс. руб. через два года наращением по простым процентам по процентной ставке 25%? Чему равен дисконт?
Решение:
Используем расчет наращения простыми процентами.
Базовая формула , где
Rn – возвращаемая сумма (24 тыс. рублей);
P – исходная сумма (искомое);
n – число лет начисления процентов (2 года);
r – годовая процентная ставка (25 %).
Преобразуем исходную формулу для вычисления неизвестного (P).
Получаем 
16 тыс. рублей
Дисконт, это разность между возвращаемой и исходной суммами.
Используем формулу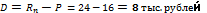 
Примечание: Обращая внимание на решение задачи 1 (выполнено по лекциям) дисконтом также может называться учетная ставка. Тогда расчет будет следующим:
0,3333= 33,33%
7. В банк 6 мая предъявлен для учета вексель на сумму 14 тыс. руб. со сроком погашения 10 июля того же года. Банк учитывает вексель по учетной ставке 40% годовых, используя способ 365/360. Определите сумму, которую получит векселедержатель от банка и комиссионные, удерживаемые банком в свою пользу за предоставленную услугу. За какое время до срока платежа операция учета векселя по учетной ставке 40% годовых имеет смысл?
Решение:
Способ 365/360 – французская практика – точное количество дней ссуды, при использовании длительности коммерческого года (360 дней). Год не високосный.
|
|
Используем расчет для коммерческого (банковского)дисконтирования.
Базовая формула 
, где
FV – возвращаемая сумма, сумма к погашению, номинальная стоимость (14 тыс. рублей);
PV – сумма покупки векселя банком (искомое);
t – количество дней до момента предъявления векселя (при точном расчете дней 191 – 126 =65 дней, с использованием таблицы порядковых номеров дней в году);
T – количество дней в году (360 дней);
d – учетная ставка (30 %).
Получаем сумму выплаты векселедержателю 
Комиссионные удерживаемые банком (дисконт) составят разницу между суммой к погашению и суммой покупки векселя банком, а именно:
D = FV – PV = 14 – 12,898 = 1,011 тыс. рублей
Операция учета имеет смысл пока сумма покупки векселя банком P больше нуля. Определим, в какой момент P станет равным нулю. Анализируя формулу банковского дисконтирования делаем вывод, что этот момент настанет, когда множитель дисконтирования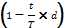 
станет равным нулю или при каком значении t будет верно равенство 
.
Получаем путем преобразования искомое 
8. Банк 7 июня учел три векселя со сроками погашения в этом же году соответственно 8 августа, 30 августа и 21 сентября. Применяя учетную ставку 25% годовых, банк удержал комиссионные в размере 2750 руб. Определите номинальную стоимость первых двух векселей, если номинальная стоимость второго векселя в два раза больше первого и третий вексель предъявлен на сумму 20 тыс. руб.
Решение:
Поскольку не определена длительность года, считаем ее равной 360 дням (коммерческий год).
Используем расчет для коммерческого (банковского)дисконтирования.
Базовая формула , где
FV – возвращаемая сумма, сумма к погашению, номинальная стоимость (FV2 = 2*FV1 (найти оба значения), FV3 = 20 тыс. рублей);
PV – сумма покупки векселя банком (неизвестно);
Комиссионные банка составили D = D1 + D2+ D3 = 2750 рублей;
t – количество дней до момента предъявления векселя (при точном расчете дней: первый вексель 220 – 158 = 62 дня, второй вексель 242 – 158 = 84 дня, третий вексель264 – 158 = 106 дней, с использованием таблицы порядковых номеров дней в году);
T – количество дней в году (360 дней);
d – учетная ставка (25 %).
Найдем D3 = FV3 - 
Получаем D1+2 = D1+D2 = D – D3 = 2750 – 1472,22 = 1277,78 рубля.
Учитывая соотношение номинальной стоимости первого и второго векселя получаем тождество:
D1+2 = D1 + D2 = FV1 - 
Выполнив математические преобразования получаем:
8000 рублей
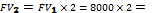16000 рублей
9. В банк 15 февраля предъявлен для учета вексель на сумму 40 тыс. руб. со сроком погашения 30 июня того же года. Банк учитывает вексель по простой процентной ставке 30% годовых. Определите сумму, полученную векселедержателем и величину дисконта банка, если при учете использовался способ 365/365 и год високосный. Каковы будут определяемые величины при учете по простой учетной ставке 30% и использовании способа 365/360?
Решение:
1) Английская практика.
Базовая формула 
, где
FV – возвращаемая сумма, сумма к погашению, номинальная стоимость (40 тыс. рублей);
PV – сумма покупки векселя банком (искомое);
t – количество дней до момента предъявления векселя (при точном расчете дней 182 – 46 =136 дней, с использованием таблицы порядковых номеров дней в високосном году);
T – количество дней в году (вариант 1 - 366);
r – процентная ставка (30 %).
Используем формулу расчета наращения простыми процентами
Преобразовываем для вычисления даты покупки
Комиссионные удерживаемые банком (дисконт) составят разницу между суммой к погашению и суммой покупки векселя банком, а именно:
D = FV – PV = 40 – 35,988 = 4,002 тыс. рублей
2) Французская практика
Базовая формула , где
FV – возвращаемая сумма, сумма к погашению, номинальная стоимость (40 тыс. рублей);
PV – сумма покупки векселя банком (искомое);
t – количество дней до момента предъявления векселя (при точном расчете дней 182 – 46 =136 дней, с использованием таблицы порядковых номеров дней в високосном году);
T – количество дней в году (вариант 2 - 360 дней);
d – учетная ставка (30 %).
Получаем сумму выплаты векселедержателю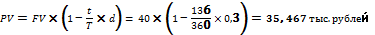 
Комиссионные удерживаемые банком (дисконт) составят разницу между суммой к погашению и суммой покупки векселя банком, а именно:
D = FV – PV = 40 – 35,467 = 4,533 тыс. рублей
10. За вексель, учтенный за 5 лет по учетной ставке 14% годовых, заплачено 4 тыс. руб. Определите номинальную величину векселя.
Решение:
Базовая формула 
, где
FV – возвращаемая сумма, сумма к погашению, номинальная стоимость (искомое);
PV – сумма покупки векселя банком (4 тыс. рублей);
n – количество лет до момента предъявления векселя;
d – учетная ставка (14 %).
Преобразуем формулу 
Получаем 
11. Найдите учетную ставку, эквивалентную простой процентной ставке 30% годовых при наращении капитала: а) за год; б) за 150 дней. Временные базы ставок одинаковы.
Решение:
Процентная ставка (норма прибыли, доходность, рост за время t) – отношение результативности сделки к исходной сумме rt = 30%.
Учетная ставка (дисконтная ставка, дисконт за время t) – отношение результативности сделки к возвращаемой сумме.
а) При rt > 0, 0 < dt < 1, rt > dt справедливы соотношения:
б) Анализируем методы расчета с использованием учетной и процентной ставок для простых процентов (краткосрочные)
Базовая формула 
Базовая формула 
FV – возвращаемая сумма;
PV – сумма покупки векселя банком (примем равной 1);
t – количество дней (150 дней);
T – количество дней в году (360, 365, 366 дней);
d – учетная ставка (искомое);
r –процентная ставка (30%).
Получаем следующее тождество:
Поскольку PV = 1 получаем:
Откуда получаем
0,2667 = 26.67%
0,2671 = 26,71%
0,2672 = 26,72%
12. Предприниматель получил в банке ссуду в размере 50 тыс. руб. на 39 месяцев под процентную ставку 27% годовых на условиях ежегодного начисления процентов. Какую сумму предприниматель должен будет вернуть банку по истечении срока при использовании схемы сложных процентов и при использовании смешанной схемы?
Решение:
а) Наращения сложными процентами можно рассчитать, используя базовую формулу:
, где
P – размер ссуды (50 тыс. рублей);
r - годовая ставка (27%);
w – число целых лет (3 года);
f – дробная часть года (0,25 года).
Получаем
108,726 тыс. рублей.
б) Наращения по смешанной схеме можно рассчитать, используя базовую формулу:
109,332 тыс. рублей.
13. Господин N инвестирует 40 тыс. руб. на 33 месяца под процентную ставку 26% годовых на условиях единовременного возврата основной суммы долга и начисленных сложных процентов. Проанализируйте, какую сумму предстоит вернуть банку при различных вариантах и схемах начисления процентов: а) полугодовое; б) квартальное.
Решение:
а) Наращения сложными процентами можно рассчитать, используя базовую формулу:
, где
P – размер ссуды (40 тыс. рублей);
r – годовая ставка (26%);
m – количество начисления процентов в год (2;4)
w – число целых периодов начисления (5; 11);
f – дробная часть периода начисления (0,5; 0).
Получаем
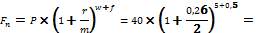78,431 тыс. рублей.
79,966 тыс. рублей.
б) Наращения по смешанной схеме можно рассчитать, используя базовую формулу:
78,488 тыс. рублей.
79,966 тыс. рублей.
14. Предлагается оформить вклад под следующие процентные ставки: 110% годовых или 22% за квартал, причем во обоих случаях используется смешанная схема начисления процентов. Какой вариант выгоднее, если срок хранения вклада составляет: а) 9 месяцев; б) один год? Финансовый год принять равным 360 дней (месяц - 30 дней).
Решение:
Наращение по смешанной схеме можно рассчитать, используя базовую формулу:
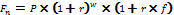, где
P – размер вклада (1);
r – годовая ставка (110%);
r4 – номинальная квартальная ставка (22%)
m – количество начисления процентов в год (1;4)
w – число целых периодов начисления (1, 3; 1; 4);
f – дробная часть периода начисления (-0,25, 0; 0; 0).
Получаем:
а)
110% годовых, 9 месяцев
1,825
22% квартальных, 9 месяцев
1,816
Выгоднее вариант с годовым начислением процентов.
б)
110% годовых, 1 год
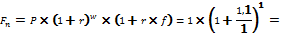2,1
22% квартальных, 1 год
2,22.
Выгоднее вариант с квартальным начислением процентов.
15. Некоторая сумма инвестируется под процентную ставку 30% годовых. Определите время, необходимое для увеличения первоначальной суммы: а) в 4 раза, б) в 2 раза при начислении в конце года сложных и простых процентов.
Решение:
Расчет наращения простыми процентами.
Базовая формула , где
Rn – возвращаемая сумма (4, 2);
P – исходная сумма (1);
n – число лет начисления процентов (искомое);
r – годовая процентная ставка (30 %).
Преобразуем исходную формулу для вычисления неизвестного (n).
Получаем 
.
Расчет наращения сложными процентами.
Базовая формула 
, где
Rn – возвращаемая сумма (4, 2);
P – исходная сумма (1);
n – число лет начисления процентов (искомое);
r – годовая процентная ставка (30 %).
Преобразуем исходную формулу для вычисления неизвестного (n).
Получаем 
а) Простые проценты при 4-х кратном увеличении капитала
.
Сложные проценты при 4-х кратном увеличении капитала
б) Простые проценты при 2-х кратном увеличении капитала
Сложные проценты при 4-х кратном увеличении капитала
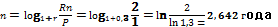
16. Вкладчик хотел бы за 7 лет утроить сумму, помещаемую в банк на депозит. Какова должна быть годовая номинальная процентная ставка при начислении сложных процентов: а) каждые полгода, б) каждый месяц.
Решение:
Расчет наращения сложными процентами при внутригодовом начислении процентов.
Базовая формула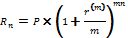 
, где
Rn – возвращаемая сумма (3);
P – исходная сумма (1);
m – число начислений сложных процентов в год (2, 12);
n – число лет начисления процентов (7 лет);
r(m) – номинальная процентная ставка, такая ставка при которой за период 1/m года, проценты начисляются по ставке rm/m (искомое).
Преобразуем исходную формулу для вычисления неизвестного (r(m)).
Получаем 
0,1633 = 16,33 %
для полугодового начисления сложных процентов и
Получаем 
0,158 = 15,80 %
для ежемесячного начисления сложных процентов.
17. В долг на 28 месяцев предоставлена сумма в 50 тыс. руб. с условием возврата 85 тыс. руб. Найдите эффективную ставку в этой финансовой сделке.
Решение:
Годовая эффективная ставка при однократном начислении сложных процентов за год обеспечивает результат как и номинальная процентная ставка. Расчет осуществляется по базовой формуле:
Номинальная процентная ставка - ставка, при которой за период 1/m года, проценты начисляются по ставке rm/m.
Базовая формула 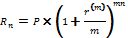, где
Rn – возвращаемая сумма (85 тыс. рублей);
P – исходная сумма (50 тыс. рублей);
m – число начислений сложных процентов (1);
n – число лет начисления процентов (28 месяцев/12 месяцев = 2,(3) года);
r(m) – номинальная процентная ставка, такая ставка при которой за период 1/m года, проценты начисляются по ставке rm/m.
Получаем
, или 
,
Откуда вычисляем искомое значение
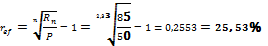
18. Из какого капитала можно получить 45 тыс. руб. через 6 лет наращением сложными процентами по процентной ставке 36%, если наращение осуществлять: а) ежегодно; б) ежеквартально?
Решение:
Расчет наращения сложными процентами при внутригодовом начислении процентов.
Базовая формула 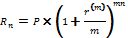, где
Rn – возвращаемая сумма (45 тыс. рублей);
P – исходная сумма (искомое);
m – число начислений сложных процентов в год (1, 4);
n – число лет начисления процентов (6 лет);
r(m) – номинальная процентная ставка, такая ставка при которой за период 1/m года, проценты начисляются по ставке rm/m (36 %).
Преобразуем исходную формулу для нахождения искомого:
при годовом начислении.
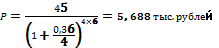
при ежеквартальном начислении.
19. Какую сумму необходимо поместить на банковский депозит, чтобы при непрерывном начислении процентов по ставке 25% получить 30 тыс. руб. через: а) 4 года; б) 9 лет?
Решение:
Расчет при непрерывном начислении процентов ведется по базовой формуле
, где
Fn – возвращаемая сумма (30 тыс. рублей);
P – исходная сумма (искомое);
e - математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. (e = 2,718281828)
n – число лет начисления процентов (4, 9 лет);
δ – непрерывная ставка (сила роста) (25 %).
Преобразуем исходную формулу для нахождения искомого:
а) 
б) 
20. Банк выдает ссуду на 7 лет под сложную процентную ставку 36% годовых с начислением процентов каждые полгода. Какую непрерывную ставку должен установить банк, чтобы за 7 лет получить тот же доход?
Решение:
Расчет наращения сложными процентами при внутригодовом начислении процентов.
Базовая формула 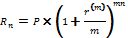, где
Rn – возвращаемая сумма (искомое);
P – исходная сумма (1);
m – число начислений сложных процентов в год (2);
n – число лет начисления процентов (7 лет);
r(m) – номинальная процентная ставка, такая ставка при которой за период 1/m года, проценты начисляются по ставке rm/m (36 %).
Определяем доход для начисления сложными процентами каждые полгода:
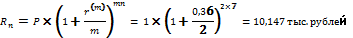
Расчет при непрерывном начислении процентов ведется по базовой формуле
, где
Fn – возвращаемая сумма (10,147 тыс. рублей);
P – исходная сумма (1);
e - математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. (e = 2,718281828)
n – число лет начисления процентов (7 лет);
δ – непрерывная ставка (искомое).
Преобразуем исходную формулу для нахождения искомого:
21. На вклад в 16 тыс. руб. начисляются непрерывные проценты. Определите наращенную сумму за 6 лет, если интенсивность наращения изменяется следующим образом: в первые два года равна 20%, следующие три года - 24% и в последний год - 26%. Какую постоянную силу роста необходимо взять, чтобы за 6 лет получить такую же наращенную сумму?
Решение:
Расчет при непрерывном начислении процентов ведется по базовой формуле
, где
Fn – возвращаемая сумма (рассчитываем);
P – исходная сумма (16 тыс. рублей);
e - математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. (e = 2,718281828)
n – число лет начисления процентов (2, 3, 1);
δ – непрерывная ставка (20 %,24 %,26 %).
Рассчитаем наращенную сумму за три периода начисления:
Преобразуем исходную формулу для нахождения решения задачи:
Более простое решение (без вычисления натурального логарифма)
Путем преобразований получаем
Искомое
22. Господин N собирается поместить на некоторый срок свободные денежные средства либо под сложную процентную ставку 30% годовых с ежеквартальным начислением процентов, либо под простую процентную ставку 48% годовых. Выясните как выгоднее поступить при сроке: а) 3 года; б) 4 года.
Решение:
Расчет наращения сложными процентами при внутригодовом начислении процентов.
Базовая формула 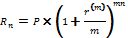, где
Rn – возвращаемая сумма (искомое);
P – исходная сумма (1);
m – число начислений сложных процентов в год (4);
n – число лет начисления процентов (3, 4 года);
r(m) – номинальная процентная ставка, такая ставка при которой за период 1/m года, проценты начисляются по ставке rm/m (30 %).
Расчет наращения простыми процентами.
Базовая формула , где
Rn – возвращаемая сумма (искомое);
P – исходная сумма (1);
n – число лет начисления процентов (3, 4 года);
r – годовая процентная ставка (48 %).
а) 
,
Выгоднее размещать денежные средства под простой процент.
б) 
,
