23. Банк принимает вклады до востребования под сложную процентную ставку 20% годовых при временной базе 365 дней. Какую простую годовую учетную ставку должен применить банк при учете векселя за 250 дней до срока его погашения, чтобы обеспечить себе такую же доходность, как и по вкладам до востребования? При учете используется временная база 360 дней.
Решение:
Расчет наращения сложными процентами.
Базовая формула 
, где
Rn – возвращаемая сумма (неизвестно);
P – исходная сумма (1);
t – число дней начислений сложных процентов (250);
T1 – количество дней в году (365 дней);
r – годовая процентная ставка (20 %).
Базовая формула 
, где
FV – возвращаемая сумма, сумма к погашению, номинальная стоимость (неизвестно);
PV – сумма покупки векселя банком (1);
t – количество дней до момента предъявления векселя (250 дней);
T2 – количество дней в году (360 дней);
d – учетная ставка (искомое).
По условиям задачи доходность от обеих операций должна быть одинаковой, следовательно используем тождество, которое преобразуем для нахождения искомого значения.
.
Получаем путем преобразований
24. Вы заняли на четыре года 10 тыс. руб. под процентную ставку 14% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определите величину годового платежа.
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.
Базовая формула 
, где
– исходная (приведенная) стоимость аннуитета (10 тыс. рублей);
A – исходная (приведенная) стоимость (искомое);
n – число периодов начисления процентов (4 года);
r –процентная ставка (14 %).
Преобразуем исходную формулу для нахождения решения задачи:
25. Вы заняли на пять лет 12 тыс. руб. под процентную ставку 12% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определите какая часть основной суммы кредита будет погашена за первые два года.
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.
Базовая формула , где
– исходная (приведенная) стоимость аннуитета (12 тыс. рублей);
A – размер аннуитета, сумма ежегодного платежа (искомое);
n – число периодов начисления процентов (5 лет);
r – процентная ставка (12 %).
Преобразуем исходную формулу для нахождения решения задачи:
| Год | Остаток основного долга на начало года, рублей | Величина годового платежа, рублей | В том числе, рублей | Остаток основного долга на конец года, рублей | |
| Проценты за год | Погашаемая часть долга | ||||
| 12000 | 3329 | 1440 | 1889 | 10111 | |
| 10111 | 3329 | 1213 | 2116 | 7995 | |
| 7995 | 3329 | 959 | 2370 | 5626 | |
| 5626 | 3329 | 675 | 2654 | 2972 | |
| 2972 | 3329 | 357 | 2972 | 0 | |
| ∑ | 16 645 | 4645 | 12000 |
Остаток основного долга на начало первого года 12000 рублей.
Начисленные проценты за первый год 12000*0,12 = 1440 рублей.
Выплачена часть основного долга 3329-1440 = 1889 рублей.
Остаток основного долга на начало первого года 12000-1889 = 10111 рубль.
Начисленные проценты за второй год 10111*0,12 = 1213 рублей.
Выплачена часть основного долга 3329-1213 = 2116 рубля.
Итого за первые два года выплачено 1889+2116 = 4005 рубля
Или 33,4%
26. Вы заняли на пять лет 10 тыс. долл. под процентную ставку 8% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определите общую сумму процентов к выплате.
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.
Базовая формула , где
– исходная (приведенная) стоимость аннуитета (10 тыс. долларов);
A – размер аннуитета, сумма ежегодного платежа (искомое);
n – число периодов начисления процентов (5 лет);
r – процентная ставка (8 %).
Преобразуем исходную формулу для нахождения ежемесячного платежа:
Общая сумма процентов равна
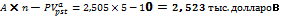
27. Предприниматель занял на шесть лет 45 тыс. руб. под 20%, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определите величину процентов, которые будут уплачены предпринимателем в четвертом году.
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.
Базовая формула , где
– исходная (приведенная) стоимость аннуитета (45 тыс. рублей);
A – размер аннуитета, сумма ежегодного платежа (искомое);
n – число периодов начисления процентов (6 лет);
r – процентная ставка (20 %).
Преобразуем исходную формулу для нахождения решения задачи:
| Год | Остаток основного долга на начало года, рублей | Величина годового платежа, рублей | В том числе, рублей | Остаток основного долга на конец года, рублей | |
| Проценты за год | Погашаемая часть долга | ||||
| 45000 | 13532 | 9000 | 4532 | 40468 | |
| 40468 | 13532 | 8094 | 5438 | 35030 | |
| 35030 | 13532 | 7006 | 6526 | 28504 | |
| 28504 | 13532 | 7831 | 20672 | ||
| 20672 | 13533 | 4134 | 9399 | 11274 | |
| 11274 | 13532 | 2258 | 11274 | 0 | |
| ∑ | 81193 | 36189 | 45000 |
Остаток основного долга на начало первого года 45000 рублей.
Начисленные проценты за первый год 45000*0,2 = 9000 рублей.
Выплачена часть основного долга 13532-9000 = 4532 рубля.
Остаток основного долга на начало первого года 45000 - 4532 = 40468 рублей. И так далее.
Начисленные проценты за четвертый год – 5701 рубль.
28. На взносы в банк каждые полгода в течение 5 лет по 1000 долл. по схеме пренумерандо банк начисляет ежеквартально проценты по сложной процентной ставке 12% годовых. Какая сумма будет на счете в конце срока?
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один раз в полгода и квартальным периодом начисления процентов.
, где
– будущая стоимость аннуитета пренумерандо (искомое);
A – размер аннуитета, сумма ежегодного платежа (1000);
n – период аннуитета (2);
m – число периодов начисления процентов, в году (4);
l – срок аннуитета (5);
r – сложная процентная ставка за период начисления (12 %).
Получаем искомое:
14042,75 долларов
Формулу вывожу следующим образом – строим геометрическую последовательность для каждого элемента аннуитета, рассчитывая наращение сложными процентами. Используя формулу суммы первых т членов геометрической последовательности получаем формулу для расчета искомого.
Где b1 первый элемент прогрессии, а q – знаменатель прогрессии.
29. Г-н N инвестировал 70 тыс. руб. в пенсионный контракт. На основе анализа таблиц смертности страховая компания предложила условия, согласно которым определенная сумма будет выплачиваться ежегодно в течение 20 лет исходя из ставки 15% годовых. Какую сумму будет получать ежегодно г-н N?
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.
Базовая формула , где
– исходная (приведенная) стоимость аннуитета (70 тыс. рублей);
A – размер аннуитета, сумма ежегодного платежа (искомое);
n – число периодов начисления процентов (20 лет);
r – процентная ставка (15 %).
Преобразуем исходную формулу для нахождения решения задачи:
30. К моменту выхода на пенсию, т.е. через 8 лет, г-н N хочет иметь на счете 30 тыс. руб. Для этого он намерен делать ежегодный взнос в банк по схеме пренумерандо. Определить размер взноса, если банк предлагает 7% годовых.
Решение:
Имеется постоянный аннуитет пренумерандо с периодом один год и равным ему периодом начисления процентов.
, где
– будущая стоимость аннуитета пренумерандо (30 тыс. рублей);
A – размер аннуитета, сумма ежегодного платежа (искомое);
n – число периодов аннуитета, равное числу периодов начисления сложных процентов (8 лет);
r – сложная процентная ставка за период начисления (7 %).
,
Преобразуем исходную формулу для нахождения искомого:
31. Стоит ли покупать за 5500 руб. ценную бумагу, генерирующую ежегодный доход в размере 1000 руб. в течение семи лет, если банк предлагает процентную ставку 8% годовых?
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.
Базовая формула , где
– исходная (приведенная) стоимость аннуитета (искомое тыс. рублей);
A – размер аннуитета, сумма ежегодного платежа (1000 рублей);
n – число периодов начисления процентов (7 лет);
r – процентная ставка (8 %).
- это меньше цены бумаги (5500 рублей), следовательно приобретать ее не стоит.
32. Предприятие приобрело здание за 20 тыс. долл. на следующих условиях: а) 25% стоимости оплачиваются немедленно; б) оставшаяся часть погашается равными годовыми платежами в течение 10 лет с начислением 12% годовых на непогашенную часть кредита по схеме сложных процентов. Определите величину годового платежа.
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.
Базовая формула , где
– исходная (приведенная) стоимость аннуитета (75% от 20 тыс. долларов = 15 тыс. долларов);
A – размер аннуитета, сумма ежегодного платежа (искомое);
n – число периодов начисления процентов (10 лет);
r – процентная ставка (12 %).
Преобразуем исходную формулу для нахождения решения задачи:
33. Г-н N хочет приобрести пенсионный контракт, по которому он мог бы получать ежегодно по 7000 руб. в течение оставшейся жизни. Страховая компания, используя таблицы смертности, оценила, что клиент сможет прожить 20 лет, и установила 6% годовых. Сколько нужно заплатить за контракт? А если установлено 8% годовых?
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.
Базовая формула , где
– исходная (приведенная) стоимость аннуитета (искомое);
A – размер аннуитета, сумма ежегодного платежа (7000);
n – число периодов начисления процентов (20 лет);
r – процентная ставка (6 %,8 %).
Стоимость контракта при ставке в 6 %:
Стоимость контракта при ставке равной 8 % годовых:
34. Раз в полгода делается взнос в банк по схеме пренумерандо в размере 500 долл. на условии 8% годовых, начисляемых каждые 6 месяцев. Какая сумма будет на счете через 5 лет? Как изменится эта сумма, если проценты будут начисляться раз в год?
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один раз в полгода и полугодовым периодом начисления процентов.
, где
– будущая стоимость аннуитета пренумерандо (искомое);
A – размер аннуитета, сумма ежегодного платежа (1000);
n – период аннуитета (2);
m – число периодов начисления процентов, в году (2, 1);
l – срок аннуитета (5);
r – сложная процентная ставка за период начисления (8 %).
Получаем искомое:
6243,18 долларов
При начислении процентов один раз в год:
6216,34 долларов
Формулу вывожу следующим образом – строим геометрическую последовательность для каждого элемента аннуитета, рассчитывая наращение сложными процентами. Используя формулу суммы первых т членов геометрической последовательности получаем формулу для расчета искомого.
Где b1 первый элемент прогрессии, а q – знаменатель прогрессии.
Ответы
1. 25%; 20%.
2. 18,18%.
3. 22,466 тыс. руб.; 22,5 тыс. руб.; 22,5 тыс. руб.
4. 1,786 года.
5. 33,75%
6. 16 тыс. руб.; 8 тыс. руб.
7. 12,989 тыс. руб.; 1,011 тыс. руб.; менее 2,5 лет.
8. 8 тыс. руб.; 16 тыс. руб.
9. 35,988 тыс. руб. и 4,012 тыс. руб.; 35,467 тыс. руб. и 4,533 тыс. руб.
10. 13,333 тыс. руб.
11. а) 23,08%; б) 26,67% (360 дней); 26,71% (365 дней); 26,72% (366 дней).
12. 108,726 тыс. руб.; 109.332 тыс. руб.
13. а) 78,341 тыс. руб.; 78,488 тыс. руб.; б) 79, 966 тыс. руб.; 79, 966 тыс. руб.
14. а) первый вариант выгоднее; б) второй вариант выгоднее
15. а) 5,284 года; 10 лет; б) 3,333 года; 2,642 года.
16. а) 16,33%; б) 15,80%.
17. 25,53%.
18. а) 7,112 тыс. руб.; б) 5,688 тыс. руб.
19. а) 11,036 тыс. руб.; б) 3,162 тыс. руб.
20. 33,10%.
21. 63,598 тыс. руб.; 23%.
22. а) под простую ставку; б) под сложную ставку.
23. 16,90%.
24. 3432 руб.
25. 4005 руб. или 33,4%.
26. 2520 долл.
27. 5701 руб.
28. 14042,76 долл.
29. 11,183 тыс. руб.
30. 2733 руб.
31. нет.
32. 2655 долл.
33. 80,290 тыс. руб. при 6%; 68,726 тыс. руб. при 8%.
34. 6243 долл.; 6216 долл.