Задание 19. Проверка гипотезы о соответствии фактического распределения нормальному
Условие. По данным интервального ряда распределения (табл. 2) проверить соответствие распределения хозяйств по урожайности нормальному, закону распределения.
Методика выполнения:
Проверка любой статистической гипотезы предполагает выполнение следующих этапов:
1. Описание статистической модели – в данном случае имеется совокупность независимых наблюдений, распределение которых неизвестно.
2. Формулируются гипотезы: нулевая (рабочая) гипотеза Но – фактическое распределение соответствует нормальному. Альтернативная гипотеза Н1- фактическое распределение существенно отличаются от нормального.
3. Устанавливается уровень значимости a, при котором будет приниматься или отвергаться гипотеза. В данном случае a=0,05.
4. Выбор подходящего статистического критерия для проверки выдвинутой гипотезы. Наиболее мощным критерием для проверки гипотезы Н0является параметрический критерий х2.
5. Определение из всей совокупности возможных значений выбранного критерия области согласия с нулевой гипотезой Н0 и критической области или области отказа от нулевой гипотезы. В данном случае критическая область – все значения, лежащие выше 5% точки распределения х2 с соответствующим числом степеней свободы.
6. Расчет по определенному алгоритму фактического значения критерия.
6.1. Фактическое значения критерия определяется по формуле
,
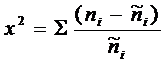где 
- фактические частоты по интервалам;
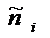- ожидаемые согласно нормальному распределению частоты.
При расчете фактического значения х2 необходимо иметь в виду, что в каждом интервале должно быть не менее одного наблюдения, а интервалов с числом наблюдений и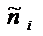 
меньше 5 не более 20 % от их общего числа.
Чтобы выполнялось это условие для учебных целей целесообразно фактические частоты интервального ряда увеличить в 2 – 3 раза. Последовательность расчетов оформляется в табл. 21.
Таблица 21 – Расчет критерия х 2
| хi | хi+1 | ni | 
| 
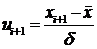
| j(ui) | j(ui+1) | рi=j(ui+1)- j(ui) |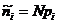 
| 
| ()2
| () 2
| 
|
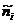
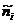
| ¥ | ¥ | -0.5000 | +0,5000 | |||||||||
| Х | Х | N= | Х | Х | Х | Х | р=1 | N= | Х | Х |
6.2. Вычислить нормированное отклонение по нижней и верхней границе каждого интервала по формулам в графах 4 и 5 табл. 21.
где хi и х i+1 – границы интервалов;
- среднее значение ряда распределения (задание 6);
d - среднее квадратическое отклонение (задание 7).
6.3. Определить вероятность попадания «Х» в интервалы Х i - Х i+1 по формуле рi =j(ui+1) - j(ui), в которой
j(u)=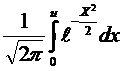 
- функция Лапласа (прил.12.)
6.4. Найти значение теоретических частот и критерия по формулам, указанным в графах 9-12 табл.21.
6.5. Произвести контроль вычисления значения критерия х 2 по формуле 
7. Сопоставить фактическое значение критерия с табличными, сделать заключение, в какой области (согласия или критической) находится фактическое значение критерия, о принятии или отказе от нулевой гипотезы с вероятностью ошибаться в своих выводах, равной a.
Табличное значение х 2 (прил.13) определяется уровнем значимости и числом степеней свободы:
к = m-1-ч
где к - число степеней свободы;
m – число интервалов ряда распределения с учетом укрупнения;
ч – число параметров, определяющих теоретическое распределение (
, d).
К=; a =; х2=
8. Сформулировать вывод о соответствии фактического распределения нормальному, закону распределения.