Контрольная работа № 1.
Ребенок играет с карточками, на каждой из которых написана одна из букв: С, Х, Р, А, А, А. Определить вероятность того, что мы сможем прочесть слово «САХАРА» при случайном расположении им карточек в ряд.
Решение:
Вероятность того, что первой карточкой окажется карточка с буквой «С» по классическому определению вероятности равна
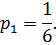
Далее, вероятность того, что второй карточкой окажется карточка с буквой «А» по классическому определению вероятности равна
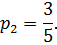
Вероятность того, третьей карточкой окажется карточка с буквой «Х» по классическому определению вероятности равна
Вероятность того, что четвертой карточкой окажется карточка с буквой «А» по классическому определению вероятности равна
Вероятность того, что пятой карточкой окажется карточка с буквой «Р» по классическому определению вероятности равна
Вероятность того, что последней карточкой окажется карточка с буквой «А» по классическому определению вероятности равна
Пусть событие 
«ребенок из карточек сложил слово САХАРА». Вероятность этого события найдем, используя теорему умножения вероятностей:
Ответ: 
С целью привлечения покупателей компания «Кока-кола» проводит конкурс, согласно которому каждая десятая бутылка напитка, является призовой. Составить закон распределения числа призовых из четырех приобретенных покупателей бутылок.
Найти математическое ожидание и дисперсию этой случайной величины. Построить функцию распределения.
Решение:
Случайная величина 
число призовых бутылок из четырех приобретенных, может принимать следующие значения: 0, 1, 2, 3, 4.
Используя формулу Бернулли
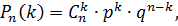
найдем соответствующие вероятности.
В нашем случае:
Вычисляем:
Запишем закон распределения:
| |||||
| 0,6561 | 0,2916 | 0,0486 | 0,0036 | 0,0001 |
Находим математическое ожидание:
Находим дисперсию:
Составим функцию распределения:
Построим график функции распределения:
Ответ: 
.
3. Найти математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины ξ, если известно, что 
и 
Построить кривую распределения этой случайной величины и найти ее максимум.
Решение:
Для нормально распределенной случайной величины с математическим ожиданием 
и средним квадратическим отклонением 
, вероятность попадания в интервал 
можно определить по формуле:
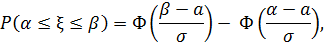
где 
функция Лапласа.
Из условия задачи имеем:
значит,
из таблицы значения функции Лапласа, учитывая, что функция нечетная, находим: 
. Тогда
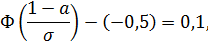
Из таблицы значения функции Лапласа определяем:
Также из условия следует:
из таблицы значения функции Лапласа находим: 
. Тогда
Из таблицы значения функции Лапласа определяем:
Чтобы найти математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины ξ, составим и решим систему уравнений:
Построим кривую распределения этой случайной величины:
Максимум находится в точке 
и равен:
4. В районном отделении Сбербанка хранят вклады 80% работающих на заводе. Какова вероятность того, что из 900 наудачу выбранных работников завода в этом отделении Сбербанка хранят вклады:
а) от 600 до 700 человек;
Б) 750 человек?
Решение:
а) Для определения искомой вероятности используем интегральную формулу Муавра-Лапласа:
где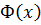 
– функция Лапласа.
По условию задачи имеем:
Тогда получим:
так как функция Лапласа нечетная, то
Используя таблицу значений функции Лапласа, находим:
Следовательно,
б) используем локальную теорему Муавра-Лапласа
где 
– функция Гаусса.
В нашем случае имеем:
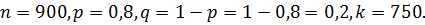
Тогда получим:
Используя таблицу значений функции Гаусса, находим:
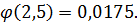
Следовательно,
Ответ: а) 0,0475; б) 0,00146.
Сумма вклада клиента сберегательного банка – это случайная величина с математическим ожиданием 15 тыс. руб. и дисперсией 0,4. Используя неравенство Чебышева, оценить вероятность того. что сумма вклада наудачу взятого вкладчика будет заключена в границах от 14 тыс. руб. до 16 тыс. руб.
Решение:
Используем формулу:
где 
функция Лапласа.
По условию задачи:
Находим:
по таблице значений функции Лапласа находим: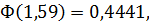 
тогда искомая вероятность равна:
Ответ: 0,882.