Задача 23 (демонстрационный вариант 2017 г).
Постройте график функции 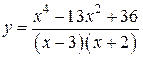 и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Решение. Разложим числитель дроби на множители:

При 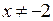 и
и  функция принимает вид:
функция принимает вид:  ,
,
её график — парабола, из которой выколоты точки  и
и  .
. 
Прямая 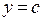 имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая. Вершина параболы имеет координаты
имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая. Вершина параболы имеет координаты  .
.
Поэтому  ,
,  или
или  .
.
Критерии оценки выполнения задания 23.
| Баллы | Критерии оценки выполнения задания |
| График построен правильно, верно указаны все значения c, при которых прямая y = c имеет с графиком только одну общую точку | |
| График построен правильно, указаны не все верные значения c | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Основным условием положительной оценки за решение задания является верное построение графика. Верное построение графика включает в себя: масштаб, содержательная таблица значений или объяснение построения, выколотая точка обозначена в соответствии с ее координатами.
Пример оценивания решения задания 23.
Постройте график функции  и определите, при каких значениях k прямая
и определите, при каких значениях k прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Ответ: 81.

Комментарий.
График построен неверно – отсутствует выколотая точка. В соответствии с критериями – 0 баллов.
Оценка эксперта: 0 баллов.
Задача 24 (демонстрационный вариант 2017 г).
В прямоугольном треугольнике  с прямым углом
с прямым углом  известны катеты:
известны катеты: 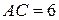 ,
,  . Найдите медиану
. Найдите медиану  этого треугольника.
этого треугольника.

|
Решение.

Ответ: 5.
Критерии оценки выполнения задания 24.
| Баллы | Критерии оценки выполнения задания |
| Получен верный обоснованный ответ | |
| При верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Задание 24 практически не менялось в течение нескольких лет. Критерии его оценивания сохранились.
Пример оценивания решения задания 24.
Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба.
Ответ: 10.

Комментарий.
Учащийся использует данные, которых нет в условии (считая острый угол ромба 60°).
Оценка эксперта: 0 баллов.
Задача 25 (демонстрационный вариант 2017 г).
В параллелограмме  точка
точка  — середина стороны
— середина стороны 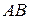 . Известно, что
. Известно, что  . Докажите, что данный параллелограмм — прямоугольник.
. Докажите, что данный параллелограмм — прямоугольник.

|
Доказательство. Треугольники  и
и  равны по трём сторонам.
равны по трём сторонам.
Значит, углы 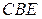 и
и 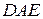 равны. Так как их сумма равна
равны. Так как их сумма равна  , то углы равны
, то углы равны  . Такой параллелограмм — прямоугольник.
. Такой параллелограмм — прямоугольник.
Критерии оценки выполнения задания 25.
| Баллы | Критерии оценки выполнения задания |
| Доказательство верное, все шаги обоснованы | |
| Доказательство в целом верное, но содержит неточности | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Пример оценивания решения задания 25.
Пример.
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.

Комментарий.
Не доказано, что точка F лежит на высоте EK.
Оценка эксперта: 0 баллов.
Задача 26 (демонстрационный вариант 2017 г).
Основание  равнобедренного треугольника
равнобедренного треугольника  равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания
равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания  . Найдите радиус окружности, вписанной в треугольник
. Найдите радиус окружности, вписанной в треугольник  .
.
Решение.

|
Пусть  — центр данной окружности,
— центр данной окружности,
а  — центр окружности, вписанной в треугольник
— центр окружности, вписанной в треугольник  .
.
Точка касания  окружностей делит
окружностей делит  пополам.
пополам.
Лучи  и
и  — биссектрисы смежных углов, значит, угол
— биссектрисы смежных углов, значит, угол  прямой. Из прямоугольного треугольника
прямой. Из прямоугольного треугольника  получаем:
получаем:  . Следовательно,
. Следовательно,

Ответ: 4,5.